lim (s ↓ 1) (s-1)ζ(s) = 1

Before beginning the derivation of Kummer's class formula for cyclotomic integers, it is necessary to review one important property from the Riemann zeta function.

The content in today's blog is taken from Harold M. Edwards' Fermat's Last Theorem.

Theorem 1: lim(s ↓ 1) (s-1)ζ(s) = 1

Proof:

(1) From a previous result (see Theorem 4, here), we know that:

ζ(s) = ∑ (1/n^s) = ∏ (1 - p^-s)^-1

and that:

for s greater than 1, both sides of this equation are absolutely convergent (see Theorem 1 and Theorem 2, here).

(2) Using the Integral Test (see Theorem 1, here),

We know that if ∑ (1/n^s) converges, then ∫ (1,∞) 1/x^sdx also converges.

(3) If we define a function so that f(x) = 1/ceiling(x)^s, we can conclude that ∫ (1,∞) 1/x^s is less than ∫ (1,∞) 1/ceiling(x)^s = ∑ (n=1,∞) 1/n^s which is less than 1 + ∫ (1,∞) 1/x^sdx since:

(a) ∫ (1,∞) 1/x^s is less than ∫ (1,∞) 1/ceiling(x)^s

At each point x ≤ ceiling(x) so that at each point x^s ≤ ceiling(x)^s.



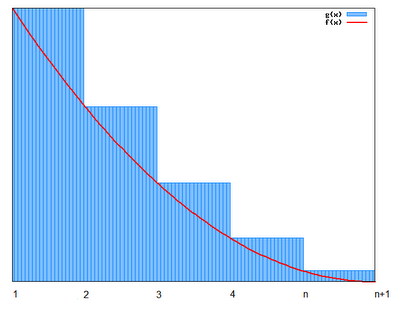
(b) ∫ (1,∞) 1/ceiling(x)^s = ∑ (n=1,∞) 1/n^s

This follows from the fact that for each interval, ∫ (x,x+1) 1/ceiling(x)^s= ∑(n=x,x) 1/n^s.

(c) ∑ (n=1,∞) 1/n^s is less than 1 + ∫ (1,∞) 1/x^sdx

This follows since ∑ (n=1,∞) 1/n^s - 1 is less than ∫ (1,∞) 1/x^sdx and therefore ∑ (n=1,∞) 1/n^s is less than 1 + ∫ (1,∞) 1/x^sdx.



(4) ∫ (1,∞) 1/x^sdx = 1/(s-1)

(a) ∫ (1,∞) 1/x^sdx = lim (t → ∞) ∫ (1,t) 1/t^sdt

(b) ∫ 1/t^sdt = ∫ t^-s dt = 1/(-s+1) (t^-s+1) + C = -1/(s-1)(1/t^s-1) + C [See here for review of integral if needed]

(c) lim (t → ∞) ∫ (1,t) 1/t^sdt = lim(t → ∞) ( [-1/(s-1)][1/t^s-1] + [1/(s-1)]*[1/1^s-1])=

= lim (t → ∞) [(-1)/[(s-1)*(t^s-1)] + [1/(s-1)]*1]

(d) As t → ∞, 1/t → 0 so we get:

= [0*(-1)/(s-1)] + [1/(s-1)] = 1/(s-1)

(5) This gives us that:

1/(s-1) is less than ζ(s) is less than 1 + 1/(s-1)

(6) Multiplying (s-1) to all sides, gives us:

1 is less than (s-1)*ζ(s) is less than (s-1) + 1 = s

(7) Now as s goes to 1, it is clear that we have:

1 ≤ (s-1)*ζ(s) ≤ 1.

(8) Using the Squeeze Law (see Lemma 3, here), we can conclude that the limit is 1.

QED

References

• Harold M. Edwards, Fermat's Last Theorem: A Genetic Introduction, Springer, 2000.
  

Euler Product Formula Converges for Re(s) > 1

To move ahead on Kummer's class number formula for ideal numbers, it is necessary to review the proof for the convergence of Euler's Product Formula, that is:

∑ n^-s = ∏ (1 - p^-s)^-1

Ernst Kummer proposed an equivalent formula for ideal numbers which I will talk about in a future blog. If you are not familiar with the notation Re(s), start here.

Theorem 1: For s greater than 1, ∑ (n=1, ∞) n^-s converges absolutely.

Proof:

(1) Let σ = Re(s)

(2) abs(n^-s) = n^-σ [See Theorem, here]

(3) Let M be any integer ≥ 1.

(4) Let N be any integer greater than M

(5) Using the triangle inequality for complex numbers (See Lemma 3, here for more details) abs[∑ (n=M+1,N) n^-s)]≤ ∑ (n=M+1,N) abs(n^-s) = ∑ (n=M+1,N) n^-σ

(6) From a previous result (See Corollary 1.2, here for more details), we know that ∑ (n=M+1,N) n^-σ converges.

*(6) Since f(x)=1/x^s is positive, continuous, and decreasing for x ≥ 1, I can use a result from an earlier blog (See Corollary 1.2, here for more details) to establish that ∑ (n=M+1,N) n^-σ converges.

(7) Since all n^-s ≥ 0, we can see that it converges absolutely. [See here for definition and properties of absolute convergence]

QED

Theorem 2: For S greater than 1, ∏(1 - p^-s) converges absolutely

Proof:

(1) ∑ abs(p^-s) = ∑(p^-σ) where σ = Re(s). [See Theorem 2, here for proof]

(2) ∑(p^-σ) ≤ ∑(n^-σ) and since ∑ (n^-σ) is convergent (by Theorem 1 above), ∑ abs(p^-s) is also convergent.

(4) ∑ abs(p^-s) is convergent implies that ∏ (1 - p^-s) is convergent. [See Lemma 6, here]

(5) And this means that ∏ (1 - p^-s)^-1 is also convergent. [See Lemma 6, here]

(6) Since ∑ abs(p^-s) is convergent, it follows that ∏(1 - p^-s) is absolutely convergent and therefore ∏ (1 - p^-s)^-1 is absolutely convergent since:

(a) Assume ∑ abs(p^-s) is convergent

(b) It follows that ∏(1 - abs[p^-s]) is convergent [See Lemma 3, here]

(c) Which means that ∏(1 - p^-s) is absolutely convergent. [See Definition 1, here]

(d) Using the Reciprocal Property of limits (see Lemma 6, here), we can see that 1/∏(1 - abs[p^-s]) is also convergent.

(e) Using the definition of absolute convergence for infinite products (see step #6c above), we see that ∏ (1 - p^-s)^-1 absolutely convergent.

QED