Newton's Identities: Vandermonde Matrix

In today's blog, I will provide a formula for obtaining the determinant of the Vandermonde matrix. For review of determinants of n x n matrices, start here.

This blog is part of the discussion of Newton's Identities. If you are interested in going to the beginning of this thread, then start here.

Definition 1: Vandermonde matrix V_n

The Vandermonde matrix is an n x n matrix where the jth column is the vector (x₁^j-1, x₂^j-1, ..., x_n^j-1).

So based on this definition, the Vandermonde matrix V_n =





Theorem 1:



Proof:

(1) Using elementary matrices (see Lemma 3, here), we know that:

I_{(-x1R1 + R2)}*I_{(-x2Rn-2 + R3)}*...*I_{(-xn-1Rn-1 + Rn)}*V_n =



(2) Using a basic property of determinants of matrices (see Definition 4, here), we know that:

det(I_{(-x1R1 + R2)}*I_{(-x2Rn-2 + R3)}*...*I_{(-xn-1Rn-1 + Rn)}*V_n) = det[I_{(-x1R1 + R2)]}*det[I_{(-x2Rn-2 + R3)}]*...*det[I_{(-xn-1Rn-1 + Rn)}]*det(V_n)

(3) Now, since det(I_{(kR1 + R2)}) = 1 (see Lemma 7, here), this gives us:

det(V_n) =



(4) We can further simplify this expression to be:

det(V_n) = det(M_1,1(V_n))

[See Corollary 3.1, here where M_1,1 is the Minor of Ent_1,1(V_n); see Definition 1 here for definition of the minor of a matrix; see Definition 1, here for definition of Ent_1,1(V_n) notation]

(5) Now, we know that M_1,1(V_n) =



=




(6) Using elementary matrices (see Corollary 4.2, here), we know that:

M_1,1(V_n) =



(7) Using step #4 gives us:

det(V_n) = det(M_1,1(V_n) =



(8) Since det(I_(kCi)) = det(I(kR_i) = k [see Theorem 9, here; see Lemma 4, here], we have:

det(V_n) =



(9) So, we have found ourselves in the same situation as step#1 except that we have eliminated x₁ as a column.

(10) If we repeat, the same process, we ultimately get:

det(V_n) =



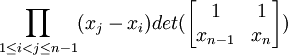
(11) So, using the determinant formula for 2 x 2 matrices (see Property 5, here; see Lemma 1, here), we have:



QED

References

• "Vandermonde Matrix", Wikipedia.org
• "Proof of the Determinant of the Vandermonde Matrix", PlanetMath.org
• "Determinants", Toomas Lepikult, at http://www.cs.ut.ee/~toomas_l/