Lemma 1: x3 = bx + c → ∃ u,v such that: b=3uv, c=u3 + v3, x = u + v
Proof:
(1) Let x3 = bx + c.
(2) Let x = u + v
(3) (u + v)3 = u3 + 3u2v + 3uv2 + v3 = 3uv(u + v) + (u3 + v3)
(4) 3uv(u + v) + (u3 + v3) = b(u + v) + c
(5) So that b = 3uv and c = u3 + v3
QED
Lemma 2: if b=3uv and c=u3 + v3, then:
we can assume:
u3 = c/2 + √(c/2)2 - (b/3)3
v3 = c/2 - √(c/2)2 - (b/3)3
Proof:
(1) b=3uv → v = b/3u
(2) u3 + v3 = u3 + (b/3u)3 =
= u3 + b3/(27u3) = c
(3) So that we have:
u3 + b3/(27u3) - c = 0
(4) Multiplying both sides by u3 gives us:
u6 + b3/27 - cu3 = 0
(5) Using the solution for quadratic equations (see here) gives us:
u3 = (c/2) ± √(c/2)2 - (b/3)3
(6) Since u3 + v3 = c, we can assume that:
u3 = (c/2) + √(c/2)2 - (b/3)3
v3 = (c/2) - √(c/2)2 - (b/3)3
QED
Theorem: Solution of the Depressed Cubic
if:
x3 + bx = c
then:
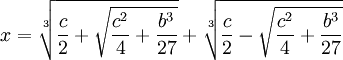
Proof:
(1) x3 + bx = c
(2) So that we have:
x3 = (-b)x + c
(3) Using Lemma 1 above, we see that there exists u,v such that:
x = u + v
(-b) = 3uv
c = u3 + v3
(4) Using Lemma 2 above, we see that:
u3 = (c/2) + √(c/2)2 - (-b/3)3 = (c/2) + √(c/2)2 + (b/3)3
v3 = (c/2) - √(c/2)2 - (-b/3)3 = (c/2) - √(c/2)2 + (b/3)3
(5) Since x = u+v, we have:
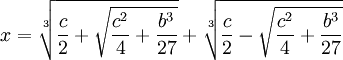
QED
No comments:
Post a Comment