Solution to the general cubic equation

Girolamo Cardano was able to find a general solution to the cubic equation based on Nicolo Fontana Tartaglia's solution to the depressed cubic equation.

For an equation of the form x³ + bx² + cx + d = 0, Cardano did this by setting x = y - b/3.

The solution is complicated. Still, this solution was a very important step forward past the mathematics of Ancient Greece. Additionally, it would lead eventually to the acceptance of imaginary numbers and the establishment of group theory.

Lemma 1: Cardano's simplification of general cubic equation

If:

x³ + bx² + cx + d = 0

Then there exists y,p,q such that:

y³ + py + q = 0

Proof:

(1) x³ + bx² + cx + d = 0

(2) Let y = x + b/3

(3) Then, x = y - b/3

(4) x³ = (y - b/3)³ = y³ - 3by²/3 + 3b²y/9 - b³/27 =

= y³ - by² + b²y/3 - b³/27

(5) bx² = b(y - b/3)² = by² - 2b²y/3 + b³/9

(6) x³ + bx² = y³ - b²y/3 + 2b³/27

(7) x³ + bx² + cx + d =

= y³ - b²y/3 + 2b³/27 + c(y - b/3) + d =

= y³ + (c - b²/3)y + (2b³/27 - bc/3 + d)

(8) Let:

p = c - b²/3

q = 2b³/27 - bc/3 + d

QED

Theorem: Solution to General Cubic Equation

If:

ax³ + bx² + cx + d = 0

Then:



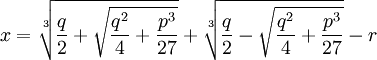
where:








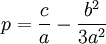
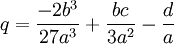
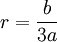
Proof:

(1) ax³ + bx² + cx + d = 0

(2) If we divide all sides by a, we get:

x³ + (b/a)x² + (c/a)x + (d/a) = 0

(3) Then using Lemma 1 above, if we set:

y = x - (b/a)/3

p = (c/a) - (b/a)²/3

q = -2(b/a)³/27 + (b/a)(c/a)/3 - (d/a)

Then we have:

y³ + py - q = 0

or:

y³ + py = q

(4) Now, using the solution for the depressed cubic (see Theorem, here),

we have:



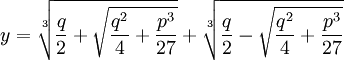
(5) Finally, adjusting for step #3, if we let:

r = (b/a)/3

Then we have:



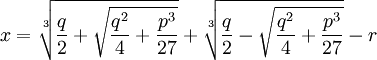
QED