Bernoulli Numbers

The Bernoulli numbers were first identified by Jakob Bernoulli in Ars Conjectandi, a work that was published after his death. The Bernoulli numbers turn up again and again in the history of mathematics. In today's blog, I will focus on the original problem that Jakob Bernoulli was attempting to solve. In a future blog, I will show how they were used by Ernst Kummer as a criteria for determining if a prime is regular.

Interestingly, Bernoulli numbers may have been discovered earlier by Seki Kowa and were rediscovered independently by a 17-year-old Srinivasa Ramanujan.

Bernoulli was analyzing formulas for the sums of powers, that have the following form:

S_m(n) = ∑ (i=1, n) i^m

He looked at, for example:

S₀(n) = n

S₁(n) = (1/2)n² - (1/2)n

S₂(n) = (1/3)n³ - (1/2)n² + (1/6)n

S₃(n) = (1/4)n⁴ - (1/2)n³ + (1/4)n²

S₄(n) = (1/5)n⁵ - (1/2)n⁴ + (1/3)n³ - (1/30)n

S₅(n) = (1/6)n⁶ - (1/2)n⁵ + (5/12)n⁴ - (1/12)n²

S₆(n) = (1/7)n⁷ - (1/2)n⁶ + (1/2)n⁵ - (1/6)n³ + (1/42)n.

S₇(n) = (1/8)n⁸ - (1/2)n⁷ + (7/12)n⁶ - (7/24)n⁴ + (1/2)n²

S₈(n) = (1/9)n⁹ - (1/2)n⁸ + (2/3)n⁷ - (7/15)n⁵ + (2/9)n³ - (1/30)n

S₉(n) = (1/10)n¹⁰ - (1/2)n⁹ + (3/4)n⁸ - (7/10)n⁶ + (1/2)n⁴ - (3/20)n²

S₁₀(n) = (1/11)n¹¹ - (1/2)n¹⁰ + (5/6)n⁹ - n⁷ + n⁵ - (1/2)n³ + (5/66)n.

By looking at these formulas, he noticed a pattern and in analyzing this pattern, he came up with what were termed Bernoulli numbers by Abraham de Moivre.

Well, for each S_m(n), we can see that:

1) the first term is 1/(m+1)*n^m+1

2) the second term, when it exists, is (-1/2)n^m

3) the third term, when it exists, is (m/12)*n^m-1

4) the fourth term, when it exists, is (-m)(m-1)(m-2)/720*n^m-3

Bernoulli had discovered that if he defined a sequence of the numbers, he got a simple formula for defining the sum of powers.

The formula he discovered was the following:



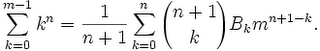
In the above formula, B_k refers to the sequence of Bernoulli numbers where Bernoulli numbers are defined in the following way:

Definition 1: Bernoulli Numbers



with B₀ = 1.

As a convention, I will refer to Bernoulli numbers as B_i.

So, to figure out, B₁, we have:



This gives us:

2*B₀ + 2*B₁ = 0

B₁ = (1/2)[-2*B₀] = (-1/2)(1) = (-1/2)

We determine B₂ based on solving:



In this way, we find that:

B₀ = 1
B₁ = -(1/2)
B₂ = (1/6)
B₃ = 0
B₄ = -(1/30)
B₅ = 0
B₆ = (1/42)
B₇ = 0
B₈ = -(1/30)
B₉ = 0
B₁₀ = (5/66)
B₁₁ = 0
B₁₂ = -(691/2730)

Bernoulli wrote that he was able to use his formula to compute S₁₀(1000) in less than 10 minutes (see Smith, A Source Book in Mathematics, below).

Using his formula, this comes down to:





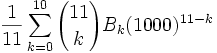
Evaluating this gives us:

91,409,924,241,424,243,424,241,924,242,500

I will now show a proof for Bernoulli's formula for sums. This is taken straight from Graham et al. Concrete Mathematics.

Definition 2: S_m(n)

Let S_m(n) = 0^m + 1^m + ... + (n-1)^m

I will use this shorthand in the lemma and theorem below.

Postulate 1: 0⁰ = 1

(This is taken from Graham et al.)

Graham et al argue in Concrete Mathematics that if we let 0⁰ = 1, it provides a more elegant notation for the Binomial Theorem. Their argument is that the Binomial Theorem is very important while 0⁰ is almost irrelevant. (see Concrete Mathematics, page 162).

Lemma 1:



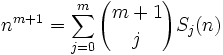
Proof:

(1) S_m+1(n) + n^m+1 =

= ∑(k=0,n-1) k^m+1 + n^m+1 =

= ∑(k=0,n) k^m+1 =

= 0^m+1 + ∑(k=1,n) k^m+1 = ∑(k=1,n) k^m+1 =

= ∑ (k=0,n-1) (k+1)^m+1

(2) Using the Binomial Theorem, we get:



(3) Putting this together with step #1 gives us:



This gives us:



(4) Since S_j(n) = o^j + 1^j + ... + (n-1)^j, we have shown that:



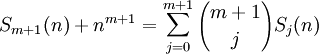
(5) Now, since



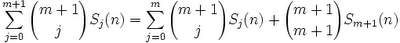
The conclusion follows from simple subtraction since [(m+1)!]/[(m+1)!(0)!] = 1.

QED

Theorem:



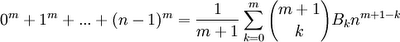
Proof:

(1) We can see that this is true for m=0 since:

S₀ = n = (1/[1+1])∑ (k=0,0) ([0+1]!/k![1-k]!)B_kn^0+1-k =

= (1)*(1!/[0!][1!])B₀n¹ = (1)*(1)*(1)*n = n [Since B₀ = 1, see above]

(2) Let's assume that this is true up to m-1.

(3) Let T_m(n) =



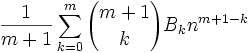
(4) Let Δ = S_m(n) - T_m(n)

(5) Using Lemma 1 above, we know that:



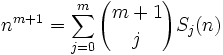
(6) Using our definition of Δ, we can also see that:



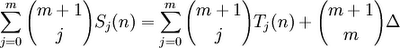
(7) The goal in this proof will be to show that Δ = 0.

(8) Adding the definition of T_j(n) [see step#3] gives us:



I also simplified [(m+1)!/(m!)(1!)] to (m+1).

(9) We can move all values that are independent of k before the ∑ (k=0,j):



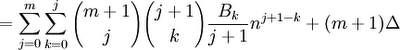
(10) Since we can change the order of the terms of a finite sum and still get the same result, we can switch each value of k with (j-k) to get:






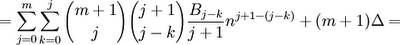
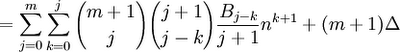
(11) Now, since (j+1) - (j-k) = k+1, we have:



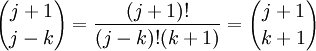
(12) Putting this result in step #11 gives us:



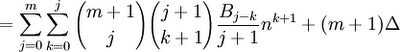
(13) We can see that in step #12, 0 ≤ k ≤ j ≤ m. The sum is in fact all combinations of j,k where this is the case. This means that we can rearrange the sum to the following:



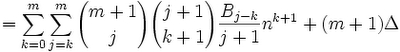
(14) Since n^k+1 is independent of j, we can move it over to get the following:



(15) Since,



we can also rearrange the result in step #14 to give us:



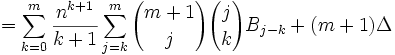
(16) Since:











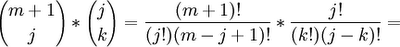
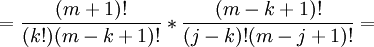
We can rearrange terms to get:



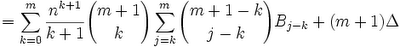
(17) Since:



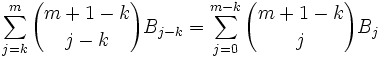
We can rearrange terms to get:



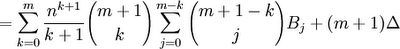
(18) Now, we know from the definition of Bernoulli numbers (see Definition 1 above) that



in all cases except where m = 0. This occurs only when k = m.

This allows us to simplify the result in step #17 to the following:



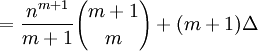
(19) Now since [(m+1)!/(m!)(1!)] = m+1, we get:

= n^m+1 + (m+1)Δ

(20) But in step #5, we started out with n^m+1 so we are left with:

n^m+1 = n^m+1 + (m+1)Δ.

(21) The only way that this is true is if Δ = 0.

QED

In another blog, I show how z/[e^z - 1] can be used as a generating function for the Bernoulli numbers.

References

• Ronald L. Graham, Donald E. Knuth, Oren Patashnik, Concrete Mathematics, Addison-Wesley, 1989
• David Eugene Smith, A Source Book in Mathematics, Dover, 1959
• "Bernoulli Numbers", Wikipedia.Com