The proof presented here relies on the Principle of Mathematical Induction. If you are not familiar with Mathematical Induction, then you may wish to start here.
The proof is based on factorials. Importantly, it relies on the following definition:

With this definition in mind, let's take a look at the proof for the Binomial Theorem:
Theorem: Binomial Theorem
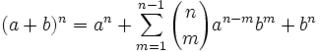
(1) The assumption here is that n ≥ 2. For n=1, we know that (a+b)1 = a1 + b1 = a + b.
(2) Let S be the set of all numbers n ≥ 2 that supports the binomial theorem. If there are no such numbers, then S would be empty.
(3) We know that 2 is an element of S since:
(a) (a + b)2 = a2 + 2ab + b2 (See here for details if needed)
(b)
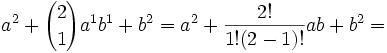
= a2 + 2ab + b2
(4) So, let us suppose that there is a value n such that 2 thru n, the binomial theorem holds. If the binomial theorem, for example, didn't hold for 3, then n would equal 2.
(5) Now, we note that:
(a + b)n+1 = (a + b)n(a + b) = a(a + b)n + b(a + b)n
(6) Now, by (4), we have:


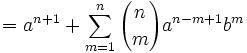
and

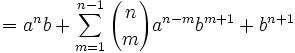
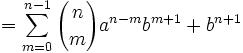
(7) The trick comes down to realizing that:
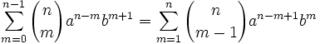
(a) We notice that m=0 thru n-1 and m=1 thru n contains the same number of elements.
(b) At each point, m as a value of the factorial expression is the same. In the case of m = 0, the first element is 0, the second element is 1, and so on until we get to n-1. In the case of m=1, the first element is 0, the second element is 1, and so on until we get to n.
(c) At each point, the exponent for a is the same. In the case of m=0, the first exponent is n-m = n, the second coefficient has a power of n-1, followed by n-2, and so on until we get to n-(n-1) = 1. In the case of m=1, the first exponent is n-m+1=n, the second coefficient has a power of n-1 and so on until we get to the last one which is n-n+1 which is equal to 1.
(d) Finally, at each point, the exponent for b is the same. In the case of m=0, the first power of b is 1, followed by 2, and so on until we get to n-1+1 which = n. In the case of m=1, the first power of b is 1, followed by 2, and so until we get to the end which b to the power of n.
(8) Applying our results from (6) and (7) and applying Pascal's Rule, we note that:
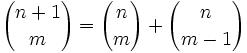
Which gives us that:

(9) And putting this all together, gives us:

QED

No comments:
Post a Comment