A Generating Function for the Bernoulli Numbers

In my previous blog, I defined the Bernoulli numbers using a recurrence relation:

In today's blog, I will show how the Bernoulli numbers can be used with a generating function. A generating function is a power series, that is, a compact expression that defines an infinite sum. For background on generating functions, I recommend the wikipedia article (see reference) or Graham et al's Concrete Mathematics (see reference).

The content in today's blog is taken from Concrete Mathematics. The term "binomial convolution" is taken from this work. A "convolution" is the multiplication of two generating functions. This lemma is called a "binomial convolution" by Graham et al because the result involves binomial coefficients (see binomial theorem, here, for more details).

Lemma 1: Binomial Convolution

Let:





h(z) = f(z)*g(z)

Then there exists d_n such that:



with:



Proof:

(1) Multiplying f(z) with g(z) gives us:



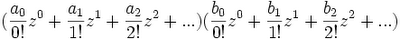
(2) Grouping the result by zⁱ gives us:



(3) If we set c_i to each coefficient. For example, if we set c₀ to (a₀b₀)/(0!0!), then we have the following formula:



(4) Now, let's define a value d_i such that:



(5) This then gives us that:
d_i/(i!) = c_i


(6) Combining step #5 with step #2 and step #3 gives us:



QED

Thereom: Generating Function for the Bernoulli Numbers

z/(e^z - 1) is the generating function for the Bernoulli numbers

Proof:

(1) Let G(z) = ∑ (n ≥ 0) B_nzⁿ/n! where B_i is the Bernoulli number for i.

(2) We know from a previous result (see Lemma 2, here) that:

e^z = ∑ (n ≥ 0) zⁿ/n!

(3) So we can use Lemma 1 above to show that:



(4) Now, the definition for Bernoulli numbers (see Definition 1, here) is:



for all cases except for B₀ where B₀ = 1.

(5) If we let n=m+1 and add B_n to both sides, then we have:



or B_n + 1 in the case where n=m+1=1.

(6) This enables us to simplify the result in step #3 to get:



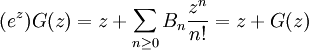
Note: the z at the bottom comes from the fact that at n=1, our result is (B₁+1)z¹/1! = B₁z¹/1! + z.

(7) If we subtract G(z) from both sides, we get:

(e^z)G(z) - G(z) = z =

G(z)(e^z - 1) = z

(8) Dividing both sides by e^z - 1 gives us:

G(z) = z/(e^z - 1)

QED

Corollary: B_2i+1=0 if i ≥ 1.

Proof:

(1) z/(e^z - 1) = ∑ (n ≥ 0) B_nzⁿ/n! [This follows from the theorem above]

(2) Now, B₁ = -(1/2) [See Definition 1, here]

(3) So,

z/(e^z - 1) + (z/2) = ∑ (n ≥ 0 and n ≠ 1) B_nzⁿ/n!

We subtract (-z/2) instead of -1/2 because we are removing this item from a generating function where each value in the sum z/(e^z-1) pairs up with a unique term of the sum.

In this case, B₁ matches up with the term B₁(z¹)/1! which equals -z/2.

(4) z/(e^z - 1) + (z/2) = (2z + z[e^z - 1])/(2[e^z-1]) = (2z -z + z[e^z])/(2[e^z-1]) =

= (z/2)(e^z+1)/(e^{z - 1})

(5) (z/2)(e^z + 1)/(e^z-1) = [e^-(z/2)/e^-(z/2)]* (z/2)(e^z + 1)/(e^z-1) =

= (z/2)[(e^z/2 + e^-z/2)/(e^z/2 - e^-z/2)]

(6) So, we see in step #5, that if we replace z with (-z), the identity remains unchanged.

(-z/2)[(e^-z/2 + e^-(-z/2)]/(e^-z/2 - e^-(-z)/2) =

= -z/2[e^-z/2 + e^z/2]/(e^-z/2 - e^z/2) =

= z/2[e^z/2 + e-z/2]/(e^z/2 - e^-z/2)

In the language of mathematics, a function is called even if f(-x)=f(x) and we call a function odd if f(-x) = -f(x). [See here for more details]

Example: cos(x) is an even function while sin(x) is an odd function. [See here for review of sin and cos]

(7) But this means that the same must hold true for ∑ (n ≥ 0 and n ≠ 1) B_nzⁿ/n!

Since by Step #3, we showed that they are equal functions.

So that we have:

∑ (n ≥ 0 and n ≠ 1) B_nzⁿ/n! = ∑ (n ≥ 0 and n ≠ 1) B_n(-z)ⁿ/n! = ∑ (n ≥ 0 and n ≠ 1) (-1)ⁿ(B_nzⁿ/n!)

(8) Matching up each of the terms according to powers of zⁿ, this gives us that:

B_n = (-1)ⁿB_n

(9) But this can only be true if B_n = 0 when n is odd.

QED

References

• "Generating Function," Wikipedia.com
• Ronald L. Graham, Donald E. Knuth, Oren Patashnik, Concrete Mathematics, Addison-Wesley, 1989
• "Odd Bernoulli Numbers are 0", PlanetMath.org
• "Even and Odd Functions", Wikipedia.com