De Moivre's Famous Formula

The simple proof of DeMoivre's Formula by Leonhard Euler does not do justice to Abraham de Moivre's important breakthrough on the roots of unity. A person viewing Euler's proof might be surprised that Sir Isaac Newton often answered questions about Principia with: "Go to Mr. de Moivre, he knows these things better than I do."

In today's blog, I will show how de Moivre derived his formula based on Francois Viete's solution of Van Roomen's Problem.

Theorem 1: De Moivre's Formula



Proof:

(1) Let x = 2 cos(α)

(2) Let l = cos(nα)

(3) We can define z such that:



(4) So that:

zⁿ = l + √l² - 1

So that:

zⁿ - l = √l² - 1

and:

(zⁿ - l)² = l² - 1

(5) Working through the equation in step #4, we get:

(zⁿ - l)² = z²ⁿ - 2lzⁿ + l² = l² - 1

Subtracting l² - 1 from both sides gives us:

z²ⁿ - 2lzⁿ + 1 = 0

(6) Now, from a Viete's famous solution to Van Roomen's problem (see Corollary 1.1, here), we have:

2 cos(nα) = f_n(2 cos α)

where:

f_n(x) =



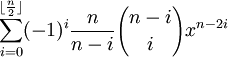
(7) Putting step #6 in step #5 gives us:

z²ⁿ - 2*(1/2)f_n(x)zⁿ + 1 = z²ⁿ - f_n(x)zⁿ + 1 =0

(8) For n=1, we have:

z²⁽¹⁾ - f₁(x)z¹ + 1 = 0

(9) Now using the definition for f_n(x) in step #6 above, we can see that:

f₁(x) = (-1)⁰(1/[1-0])([1-0]!/0![1 - 2*0]!)x^{1 - 2*0} =

= 1*(1/1)(1!/[0!1!])x¹ =

= x

(10) This then gives us:

z² - xz + 1 = 0

(11) Now using the quadratic equation to solve for z (see Theorem, here) gives us:

z = (x ± √x² - 4)/2 =

= x/2 ± √(x/2)² - 1

(12) Since x = 2cos(α), this gives us:

z = [2 cos(α)]/2 ± √[2 cos(α)/2]² - 1 =

= cos(α) ± √cos²(α) - 1

(13) Since cos²(x) + sin²(x) = 1 [See Corollary 2, here], we have:

z = cos(α) ± √cos²(α) - 1 =

= cos(α) ± √(-1)[1 - cos²(α)] =

= cos(α) ± √(-1)sin²(α) =

= cos(α) ± [√(-1)]sin(α)

(14) Since l = cos(nα), from step #2 above, we have:












(15) Putting step #13 and step #14 together gives us:



QED

You might notice that De Moivre's result is ambiguous. Since there are n roots, it is impossible that its result could only be two possible values. This problem was not evident until after there was deeper understanding of the fundamental theorem of algebra. Interestingly, this fundamental theorem was not well understood until after De Moivre's discovery of the roots of unity which I will talk about in my next blog.

The corrected version of de Moivre's formula is:

cos(nα) + isin(nα) = [cos(α) + isin(α)]ⁿ

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001