Gauss: Q(μp)

In today's blog, I will review some basic properties of Q(μ_p) which is the set of complex numbers which are rational expressions in the p-th roots of unity.

The content in today's blog is taken straight from Jean-Pierre Tignol's Galois Theory of Algebraic Equations. I will later use the results in today's blog in the proof by Carl Friedrich Gauss that all roots of unity are expressible as radicals.

Definition 1: μ_p

Let μ_p denote the set of p-th roots of unity.

Example:

μ₁ = {1}
μ₂ = {1, -1}
μ₃ = {1, (1/2)[-1 + √-3], 1/2)[-1 - √-3])
μ₄ = {1, -1, i, -i}

Now, let's use this to define a field (see Definition 3, here for definition of a field if needed)

Definition 2: Q(μ_p)

Let Q(μ_p) denote the set of complex numbers that are rational expressions in these p-th roots of unity.

This gives us that:



Now, we can show that Q(μ_p) = Q(ζ).

Lemma 1:

Q(μ_p) = Q(ζ)

Proof:

(1) From Defintion 1 above:

μ_p = { ρ₁, ..., ρ_p}

(2) Let ζ = a primitive p-th root of unity (see Definition 2, here for definition of a primitive p-th root of unity if needed)

(3) Using Theorem 3, here, we have:

μ_p = { 1, ζ, ζ², ..., ζ^p-1 }

(4) Then we have:



QED

Lemma 2:

Let P,Q be polynomials with coefficients in field F.

If:

P is irreducible in F[X]. (See Definition 1, here, for definition of irreducible polynomials)

P,Q have a common root u in field K which contains F

Then:

P divides Q.

Proof:

(1) Assume that P does not divide Q.

(2) Then P,Q are relatively prime polynomials since P is irreducible. [See Definition 1, here for definition of irreducible polynomials]

(3) Then (see Corollary 3.1, here), there exists polynomials U,V in F[X] such that:

P(X)U(X) + Q(X)V(X) = 1

(4) Substituting the common root u into the polynomials, we get:

P(u)U(u) + Q(u)V(u) = 1 in K

(5) Since u is the root for P(X) and Q(X), this gives us that:

P(u) = 0, Q(u) = 0 in K

(6) But then:

o*U(u) + 0*V(u) = 1 in K which is impossible.

(7) Therefore we reject our assumption in step #1.

QED

Lemma 3:

If u ∈ field K is a root of an irreducible polynomial P ∈ F[X] of degree d

and



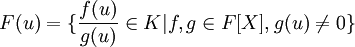
Then:

every element in F(u) can be uniquely written in the form:

a₀ + a₁u + a₂u² + ... + a_d-1u^d-1 with a_i ∈ field F.

Proof:

(1) Let f(u)/g(u) be an arbitrary element in F(u)

(2) Since g(u) ≠ 0, it follows that g(u) is not divisible by P since:

(a) Assume that g(u) is divisible by P.

(b) Since P(u) = 0, if follows that (X - u) divides P. [See Theorem, here]

(c) But if P divides g(u), then (X -u) divides g(u).

(d) But this is impossible since this implies g(u) = 0 [See Theorem, here] but g(u) ≠ 0.

(e) So we reject the assumption in step #2a.

(3) Then, g(u) is relatively prime to P since P is irreducible. [See Definition 1, here for definition of irreducible polynomials]

(4) Then (see Corollary 3.1, here), there exists polynomials h,U in F such that:

g(X)h(X) + P(X)U(X) = 1 in F[X]

(5) Since P(u) = 0, substituting u for X gives us:

g(u)h(u) + P(u)U(u) = g(u)h(u) + 0*U(u) = g(u)h(u) = 1 in K.

(6) Since g(u) ≠ 0, we have:

h(u) = 1/g(u) in K

which gives us that:

f(u)/g(u) = f(u)h(u) in K

(7) Using the Division Algorithm for Polynomials (see Theorem, here), there exists Q, R such that:

fh = PQ + R in F[X] with deg R ≤ d - 1.

(8) Since P(u) = 0, it follows that:

f(u)h(u) = P(u)Q(u) + R(u) = 0*Q(u) + R(u) = R(u) in K

(9) Since R(u) is a polynomial of degree at most d-1, we have converted an arbitrary expression f(u)/g(u) ∈ F(u) into a polynomial expression of the type:

a₀ + a₁u + ... + a_d-1u^d-1

with a_i ∈ F

(10) Now, I will prove uniqueness.

(11) Assume that:

a₀ + a₁u + ... + a_d-1u^d-1 = b₀ + b₁u + ... + b_d-1u^d-1

(12) Let us define V(X) such that:

V(X) = (a₀ - b₀) + (a₁ - b₁)X + ... + (a_d-1 - b_d-1)X^d-1 ∈ F[X]

(13) It is clear that V(u) = 0 from step #11.

(14) Using Lemma 2 above, it is clear that P divides V.

(15) But since deg V ≤ d-1 and since P is of degree d, this is impossible unless V=0.

(16) Therefore, it follows that:

a₀ - b₀ = a₁ - b₁ = ... = a_d-1 - b_d-1 = 0

QED

Theorem 4: Every element in Q(μ_p) can be expressed in one and only one way as a linear combination with rational coefficients of the p-th roots of unity other than 1:

a₁ζ + a₂ζ² + ... + a_p-1ζ^p-1

with a_i ∈ Q.

Proof:

(1) Let ζ be a root of Φ_p [See Definition 1, here]

(2) Q(μ_p) = Q(ζ) [From Lemma 1 above]

(3) Since p is a prime, Φ_p is irreducible over Q . [See Corollary 1.1., here]

(4) Using Lemma 3 above, since the degree of ζ is p-1, it follows that every element a ∈ Q(μ_p) can be uniquely expressed in the form:

a = a₀ + a₁ζ + a₂ζ² + ... + a_p-2ζ^p-2

for some a_i ∈ Q.

(5) Using the cyclotomic equation (see Lemma 1, here), we have:

Φ_p(ζ) = 1 + ζ + ζ² + ... + ζ^p-1 = 0

which means that:

ζ + ζ² + ... + ζ^p-1 = -1

(6) This gives us that:

a₀ = -a₀(ζ + ζ² + ... + ζ^p-1)

(7) Combining step #6 with step #4 gives us:

a = (a₁ - a₀)ζ + (a₂ - a₀)ζ² + ... + (a_p-2 - a₀)ζ^p-2 + (-a₀)ζ^p-1

(8) To prove uniqueness, let's assume that:

a₁ζ + ... + a_p-1ζ^p-1 = b₁ζ + ... + b_p-1ζ^p-1

(9) From step #5, we also have:

ζ^p-1 = -1 - ζ - ζ² + ... -ζ^p-2

(10) Putting this into step #8 gives us:

a₁ζ + ... + a_p-1(-1 - ζ - ζ² + ... -ζ^p-2) = b₁ζ + ... + b_p-1(-1 - ζ - ζ² + ... -ζ^p-2)

which reduces to:

-a_p-1 + (a₁ - a_p-1)ζ + (a₂ - a_p-1)ζ² + ... + (a_p-2 - a_p-1)ζ^p-2 = -b_p-1 + (b₁ - b_p-1)ζ + (b₂ - b_p-1)ζ² + ... + (b_p-2 - b_p-1)ζ^p-2

(11) From Lemma 3 above, we can conclude that the coefficients on both sides are equal which gives us:

a_p-1 = b_p-1

which then gives us:

a₁ = b₁
...
a_p-2 = b_p-2

QED

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Eisenstein: Criteria for Irreducibility of Polynomials

In today's blog, I will go over a classical result from Ferdinand Eisenstein. The content in today's proof is taken directly from Jean-Pierre Tignol's Galois' Theory of Algebraic Equations.

I will later use this result in Carl Friedrich Gauss's proof that all roots of unity are expressible as radicals.

For those who are not familiar, a monic polynomial is a polynomial whose leading coefficient is 1.

Theorem 1: Eisenstein's Criteria for Irreducibility of Polynomials

Let P be a monic polynomial with integral coefficients such that:

P = X^t + c_t-1X^t-1 + ... + c₁X + c₀ ∈ Z[X]

If there is a prime number p which divides c_i for i = 0, ..., t-1 but p² does not divide c₀

then:

P is irreducible over Q

Proof

(1) Assume that P is not irreducible over Q.

(2) Then there exist two non-constant polynomials f,g ∈ Q[X] such that:

P = fg

(3) Assume that f has degree n with n ≥ 1 and g has degree m with m ≥ 1 so that:

f = Xⁿ + a_n-1X^n-1 + ... + a₁X + a₀ ∈ Z[X]

g = X_m + b_m-1X^m-1 + ... + b₁X + b₀ ∈ Z[X]

(4) Since P is monic, we can assume that f,g are monic [if f,g are not monic, then (f/a_n is monic and a_n*g is monic since P = (f/a_n)*(g*a_n)]

(5) From step #2, it is also clear that c₀ = a₀*b₀

(6) Using Euclid's Lemma (see Lemma 2, here), it is clear that for the prime p, p divides a₀ or b₀.

(7) It is also clear that since p² does not divide c₀ that p cannot divide both a₀ and b₀.

(8) We can assume that p divides a₀ but not b₀ (if it did not, we could switch f,g since they are interchangeable with respect to p and make the same assumption)

(9) Let i be the largest index of a such that p divides a_i. It is clear that 0 ≤ i ≤ n-1. So, we can conclude that for any i, p divides a₀, a₁, ..., a_i.

(10) Let k = i+1, it is clear that 1 ≤ k ≤ n and p does not divide a_k.

(11) So:

c_i+1 = a_i+1b₀ + a_ib₁ + a_i-1b₂ + ... + a₀b_i+1.

where b_j = 0 if j is greater than m.

(12) Now i+1 ≤ n which is less than t since n+1 ≤ m+n = t [since m ≥ 1 and n ≥ 1]

(13) So it follows that i+1 ≤ t-1 and p divides c_i+1. [From the given in the theorem that p divides c₀, ..., c_t-1]

(14) So, from step #13, it follows that since p divides c_i+1 and p divides a₀, a₁, ..., a_i [step #9] that p must also divide a_i+1b₀.

(15) But this is impossible since p doesn't divide b₀ (step #8) and p doesn't divide a_i+1 [step #10]

(16) So we have a contradiction and we must reject our assumption in step #1.

QED

Corollary 1.1: For every prime p, the cyclotomic polynomial

Φ_p(x) = x^p-1 + x^p-2 + ... + x + 1

is irreducible over the field of rational numbers

Proof:

(1) From the definition of the cyclotomic polynomial (see Definition 1, here):

Φ_p(x) = (x^p - 1)/(x - 1)

(2) Setting x = y + 1, we get:

Φ_p(y+1) = ([y + 1]^p - 1)/([y + 1] - 1) =

= ([y + 1]^p - 1)/y

(3) Using the Binomial Theorem (see Theorem, here):



(4) So, combining this with step #2 gives us:












(5) Now, it is clear that for (y+1)^p all the resulting coefficients are integral (since integers are closed on additional and multiplication, see Lemma 1 and Lemma 2, here).

(6) Further, we know that for p!/[(m!)(p-m)!] where 1 ≤ m ≤ p-2, p is not divisible by (m!) or by (p-1)! [Since p is a prime and only divisible by p and m! and (p-m)! does not include p]

(7) So, we can conclude that for m=1, ..., p-2, we have p divides p!/[(m!)(p-m)!]

(8) Now, we can use Eisenstein's Criterion above to conclude that the cyclotomic polynomial is irreducible in the field Q since:

the cyclotomic polynomial is monic, p divides all coefficients except for the leading coefficient, and p² does not divide the last coefficient (p² does not divide p.)

QED

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Gauss: Gauss's Lemma for Polynomials

Today's proof is taken from Carl Friedrich Gauss' Disquisitiones Arithmeticae (Article 42). This is Gauss' classic work on number theory which he wrote when he was 21. It is a masterpiece that includes the first use of modular arithmetic, the first complete proof of the fundamental theorem of algebra, a proof for quadratic reciprocity, Gauss' analysis of cyclotomic equations, as well as the first systematic presentation of number theory.

Lemma 1:

if a prime p doesn't divide an integer a, then (a +bp)/cp is not an integer

Proof:

(1) There exists an integer d such that a ≡ d (mod p) where 1 ≤ d ≤ p-1.

(2) So, p divides a - d. (see here for review of modular arithmetic)

(3) And p divides (a - d) so p divides (a -d) + bp = (a + bp) -d

(4) So therefore a + bp ≡ d (mod p)

(5) So it follows that since p doesn't divide a+bp, then (a +bp)/cp is not an integer.

QED

A monic polynomial is a polynomial whose leading coefficient is 1 (see Definition 5, here)

Theorem 2: Gauss's Lemma for Polynomials

Let P,Q be two monic polynomials such that:

P = x^m + a₁x^m-1 + a₂x^m-2 + a₃x^m-3 + ... + a_m

Q = xⁿ + b₁x^n-1 + b₂x^n-2 + b₃x^n-3 + ... + b_n

If the coefficients of P are rational but not all integers and if the product is also monic such that:

PQ = x^m+n + c₁x^m+n-1 + c₂x^m+n-2 + c₃x^m+n-3 + ... + c_m+n

Then, the coefficients c₁, c₂, ..., c_m+n cannot all be integers.

Proof:

(1) Let us assume that all rational cofficients in a₁, ..., a_m and b₁, ..., b_n are expressed in their lowest form.

(2) Let p be a prime number that divides one of the denominators of P [we can assume this since not all the coefficients of P are integers]

(3) Since Q is monic, it is clear that the at least one of the coefficients of (Q)/p will have p as a factor of its denominator (for example, bⁿ will have (1/p) as its coefficient).

(4) In P, there will always be one term, a fraction, whose denominator involves high powers of p than all the fractional coefficients that precede it and no lower powers than the denominators of all succeeding fractional coefficients.

For example, if there is only one fraction with the rest integers, than this fraction is the coefficient. One can start with the first coefficient divisible by p and then check if there are any coefficients after it that are divisible by a greater power of p.

(5) We can identify the term in step #4 as Gx^g with G divisible by 1/(p^t) with t ≥ 1.

(6) Since p divides at least one of the denominators in (Q)/p, the same term in step #4 exists in (Q)/p.

(7) We can identify the term in step #6 as Hx^h with H divisible by 1/(p^u) with u ≥ 1.

(8) Now, it follows that t + u ≥ 2.

(9) Next, I will show that the term x^g+h in the product of (P) and (Q) will have a fractional coefficient who denominator is divisible by 1/(p^t+u-1). This then will complete the proof since a coefficient that is divisible by 1/(p^t+u-1) where p is a prime is not an integer.

(10) Let the terms in P which precede Gx^g be 'Gx^g+1, ''Gx^g+2 and those which follow Gx^g be G'x^g-1, G''x^g-2

(11) Let the terms in (Q)/p which precede Hx^h be 'Hx^h+1, ''Hx^h+2 and those which follow Hx^h be H'x^h-1, H''x^h-2

(12) If we multiply P and (Q)/p, the coefficient of the term Gx^g*Hx^h is GH + 'GH' + ''GH'' + ... + 'HG' + ''HG'' + ...

(13) Because G,H have the highest power of p, there exists e₀,f₀ such that:

p does not divide e₀
p does not divide f₀

and

GH = e₀/(f₀p^t+u)

(14) Since any of the ('G, ''G, etc.) or ('H, ''H, etc.) have a power of p less than t or u and because any of the (G', G'', etc.) or (H', H'', etc) have a power of p no greater than t or u, it follows that any product of the form ('GH', ''GH'', etc.) will have the following form:

'GH' = e_i/(f_ip^t+u-d_i)

where

p does not divide e_i
p does not divide f_i
d_i ≥ 1.

(15) Now if we sum all the factors in step #14 and reduce the denominator to the lowest term, then we get:

∑ e_i/(f_ip^t+u-d_i) =

= e'/(f'p^t+u-d'i)

where

p does not divide e'
p does not divide f'
d' ≥ 1.

(16) If we add up the result of step #14 with step #15, we get:

(e₀f' + e'f₀p^d)/(f₀f'p^t+u)

where:

p does not divide e₀
p does not divide e'
p does not divide f₀
p does not divide f'
d ≥ 1
(t + u) ≥ 2

(17) Since Q = p*(Q)/p, for this same coefficient for P*Q, we have:

(e₀f' + e'f₀p^d)/(f₀f'p^t+u-1)

where:

p does not divide e₀
p does not divide e'
p does not divide f₀
p does not divide f'
d ≥ 1
(t + u - 1) ≥ 1

(18) Since p does not divide e₀ or f', it follows that p does not divide e₀f.

(19) If:

a = e₀f'
b = ef₀p^d-1
c = f₀f'p^t+u-2

Then we can use Lemma 1 above to conclude that:

(e₀f' + e'f₀p^d)/(f₀f'p^t+u-1)

is not an integer.

QED

Corollary 2.1:

If a monic polynomial in Q[X] divides a monic polynomial with integral coefficients, then its coefficients are all integral.

Proof:

(1) Let f be a monic polynomial with integral coefficients.

(2) Let P be a monic polynomial that divides f.

(3) Since P divides f, there exists a polynomial Q such that:

f = PQ

(4) Since P,f are monic, it follows that Q must also be monic. [See Lemma 1, here]

(5) Assume that the coefficient in P are not all integers.

(6) Then, using Theorem 2 above, it follows that the coefficients of f are not all integers.

(7) But this is not correct since by assumption, all the coefficients of f are integers.

(8) So we reject our assumption in step #5.

QED

References

• Carl Friedrich Gauss, Translated by Arthur A. Clarke, Disquisitiones Arithmeticae, Yale University Press, 1965.