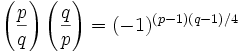
For those not familiar with quadratic reciprocity, quadratic residues, or with the notation above, start here.
Today's proof is based on the Gareth A. Jones and J. Mary Jones Elementary Number Theory.
Theorem 1: Principle of Quadratic Reciprocity.
Given p,q are odd primes. if p or q ≡ 1 (mod 4), then p is a quadratic residue of q if and only if q is a quadratic residue of p. if both p and q ≡ 3 (mod 4), then p is a quadratic residue of q if and only q is not a quadratic residue of p and likewise, q is a quadratic residue of p if and only if p is not a quadratic residue of q.
(1) Let P be the set of integers {1, 2, ... (p-1)/2 }
(2) Let N be the set of integers -P, that is, {-1, -2, ... -(p-1)/2}
(3) Let Q be the set of integers {1, 2, ... (q-1)/2 }
(4) Now by Gauss's Lemma (see here):
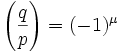
where μ is the number of elements in qP ∩ N. [See here for details on qP ∩ N]
(5) Further, we can conclude (see here):
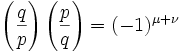
where μ + ν is the number of pairs (x,y) ∈ PxQ such that -p/2 is less than qx-py is less than q/2.
(6) From a result, I will show later, there exist values α and β such that:
μ + ν = (p-1)(q-1)/4 - (α + β).
(7) Now, it can be shown (see Lemma 2 here), that α = β
(8) With this in place, we combine (#5) with (#6) to get (see Lemma 3 here):
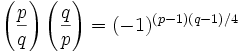
QED
Note: if you are unclear how (#8) is equivalent to the given, see here.

No comments:
Post a Comment