Proof of Solution to Depressed Cubic

In today's blog, I will show a proof of the solution to the depressed cubic equation. Using Girolamo Cardano's trick (next blog), it is possible to use the solution to the depressed cubic equation to solve the general cubic equation.

Lemma 1: x³ = bx + c → ∃ u,v such that: b=3uv, c=u³ + v³, x = u + v

Proof:

(1) Let x³ = bx + c.

(2) Let x = u + v

(3) (u + v)³ = u³ + 3u²v + 3uv² + v³ = 3uv(u + v) + (u³ + v³)

(4) 3uv(u + v) + (u³ + v³) = b(u + v) + c

(5) So that b = 3uv and c = u³ + v³

QED

Lemma 2: if b=3uv and c=u³ + v³, then:

we can assume:

u³ = c/2 + √(c/2)² - (b/3)³

v³ = c/2 - √(c/2)² - (b/3)³

Proof:

(1) b=3uv → v = b/3u

(2) u³ + v³ = u³ + (b/3u)³ =

= u³ + b³/(27u³) = c

(3) So that we have:

u³ + b³/(27u³) - c = 0

(4) Multiplying both sides by u³ gives us:

u⁶ + b³/27 - cu³ = 0

(5) Using the solution for quadratic equations (see here) gives us:

u³ = (c/2) ± √(c/2)² - (b/3)³

(6) Since u³ + v³ = c, we can assume that:

u³ = (c/2) + √(c/2)² - (b/3)³

v³ = (c/2) - √(c/2)² - (b/3)³

QED

Theorem: Solution of the Depressed Cubic

if:

x³ + bx = c

then:



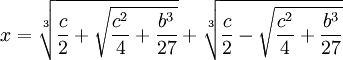
Proof:

(1) x³ + bx = c

(2) So that we have:

x³ = (-b)x + c

(3) Using Lemma 1 above, we see that there exists u,v such that:

x = u + v

(-b) = 3uv

c = u³ + v³

(4) Using Lemma 2 above, we see that:

u³ = (c/2) + √(c/2)² - (-b/3)³ = (c/2) + √(c/2)² + (b/3)³

v³ = (c/2) - √(c/2)² - (-b/3)³ = (c/2) - √(c/2)² + (b/3)³

(5) Since x = u+v, we have:



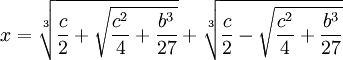
QED