Gauss: Construction of regular polygons

It was not enough for Carl Friedrich Gauss to prove the constructibility a heptadecagon (a seventeen sided polygon). He generalized the idea to come up with the theorem that I will present today.

The content in today's blog is taken from Jean-Pierre Tignol's Galois' Theory of Algebraic Equations.

Lemma 1: The periods of two terms are (2 cos 2kπ/p) for k = 1 ... (p-1)/2

Proof:

(1) η_j = ζ_j + ζ_{[j + (p-1)/2]} [See Definition 3, here where e = (p-1)/2 and f = 2]

(2) ζ_{[j + (p-1)/2]} = (ζ_j)^g(p-1)/2 [See Definition 1, here]

(3) g^(p-1)/2 ≡ -1 (mod p) since:

(a) (g^(p-1)/2)² ≡ g^p-1 (mod p)

(b) g^p-1 ≡ 1 (mod p) [By Fermat's Little Theorem, see here]

(c) Thus, g^(p-1)/2 ≡ ± 1 (mod p)

(d) But since g is a primitive root modulo p (see Definition 2 and Definition 4, here) and since (p-1)/2 is less than p-1, it follows that g^(p-1)/2 ≠ 1.

(e) Thus, we have that g^(p-1)/2 ≡ -1 (mod p).

(4) So, we have η_j = ζ_j + ζ_j^-1 [See Lemma 1, here]

(5) We can express the p-th roots of unity as solutions to Φ_p(x) such that they are the solution to:

x^p-1 + x^p-2 + ... + 1 = 0 [See Lemma 1, here]

(6) The trigonometric solution for the equation above are (see Corollary 1.1, here):

cos 2kπ/p + isin 2kπ/p where 1 ≤ k ≤ p-1.

(7) For ζ_j, there exists an integer m such that:

ζ_j = cos 2mπ/p + i sin 2mπ/p

(8) Using Lemma 4, here, where u= 2mπ/p, we have:

ζ_j + ζ_j^-1 = cos 2mπ/p + i sin 2mπ/p + cos 2mπ/p - isin 2mπ/p = 2 cos 2m π/p.

QED

Theorem 2: If p is a prime number of the form p = 2^m+1 (with m ∈ N) then the regular polygon with p sides can be constructed with ruler and compass.

Proof:

(1) Since p=2^m + 1, p-1 is a power of 2.

(2) We can thus view p-1 as a chain of multiplications such as:

1 → 2 → ... → 2^m-2 → 2^m-1 → 2^m

(3) Using a previous result (see Lemma 5, here), we can see that the chain of multiplication in step #2 shows that the periods of two terms can be determined by solving a sequence of quadratic equations.

(4) The periods of two terms are the values 2 cos 2kπ/p for k = 1 ... (p-1)/2 [See Lemma 1 above]

(5) Since the solution of a quadratic equation only requires rational operations and extraction of square roots (see Theorem, here), it follows that cos 2π/p can be obtained from 0 and 1 by rational operations and extractions of roots.

(6) So, using Wantzel's Constructibility Criterion (see Theorem 5, here), it follows that (cos 2π/p, 0) is constructible.

(7) Let A be a point at (0,a) and O at (0,0) such that we take OA as one unit of measurement and circle OA is a unit circle (see here for details if needed on unit circles)

(8) Point P0 = (cos 2π/p, sin 2π/p) is obtained in the following way:

(a) Let Q be the point at (cos 2π/p, 0) that we showed was constructible in step #6 above.

(b) Let QP0 be a line that is perpendicular to OQ and where P0 intersects with the unit circle OA. [See here for Euclid, Book I, Proposition 11 which shows this construction]

(c) Now, we can see that P0 is at (cos 2π/p, sin 2π/p) since:




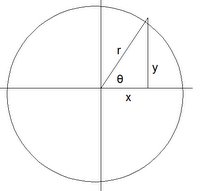
By the diagram above:

x = cos 2π/p

r = 1

Since cos θ = (cos 2π/p)/1 = cos 2π/p, we have θ = 2π/p.

Also, we have: sin θ = sin 2π/p = y/1 = y

(9) The point P0 is a vertex of the regular polygon with p sides. The line AP0 forms one side of the polygon, so we can label point A as P1.

(10) We can find the other p-1 sides in the following way. Let P0P1 be a circle at point P1 with radius equal to P0P1 (see Postulate 2, here). Call P2 the point where circle P0P1 intersects with unit circle OA (and is not point P0). We can repeat for circle P2P1 (finding point P3), circle P3P2 (find point P4), etc. until we have constructed our regular p-sided figure.

QED

Corollary 2.1: A regular polygon with n sides can be constructed with a ruler and compass if n is a product of distinct Fermat primes and a power of 2.

Proof:

(1) A regular polygon with n sides is constructible when n is a Fermat prime. [By Theorem 2 above]

(2) Since we can always do a repeated bisection of angles (see here for Euclid's Elements, Book I, Prop 9), a regular polygon with n sides is also constructible when n is a power of 2.

(3) So, to complete this proof, we only need to show that if n₁ and n₂ are relatively prime and a polygon with n₁ sides is constructible and a polygon with n₂ sides is constructible, then it follows that a polygon with n₁n₂ sides is constructible.

(4) Since n₁, n₂ are relatively prime, there exists integers m₁, m₂ such that (see Lemma 1, here):

m₁n₁ + m₂n₂ = 1.

(5) Multiplying both sides by 2π/(n₁n₂) gets us:

m₁(2π/n₂) + m₂(2π/n₁) = 2π/(n₁n₂)

(6) Therefore using Wantzel's Criterion (see Theorem 5, here), it follows that 2π/(n₁n₂) can be constructed by repeating a certain number of times 2π/n₁ and 2π/n₂.

(7) It therefore follows that the regular polygon with n₁n₂ sides can be constructed from regular n₁ polygon and a regular n₂ polygon.

QED

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001