Abel printed a limited set copies of his proof in hopes of using it as a "calling card" when he visited the great mathematicians of his day. Because he was short on funds, Abel was forced to keep the proof as short and concise as possible. He had hoped to secure recognition and financial sponsorship from his trip. When he ran out of money, he returned to his native Norway at the end of 1826.
In December of 1828, he grew very sick. He did not recover and died on April 6. Two days later, not knowing that he had died, a messenger arrived letting his family know that Abel had secured a mathematical position in Berlin. Abel was 26.
Abel was the second person to attempt this proof. His predecessor Paolo Ruffini came very close. So close, in fact, that Augustin-Louis Cauchy believed that he had succeeded. In his honor, the proof is often called the Abel-Ruffini Theorem. In fairness to Abel, Ruffini made an assumption in his proof which turns out to be true but which Ruffini did not prove.
In today's blog, I will show the argument in Abel's original proof of 1824.
Lemma 1:
Let:
(p + p1S(1/2))(1/m) + (p - p1S(1/2))(-1/m)
be a function on 5 parameters y1, ..., y5
where p,p1,S are symmetric on the same 5 parameters and m ≥ 2.
Then:
this function returns m distinct values when its parameters are permuted
Proof:
(1) By Lemma 1, here, S(1/2) takes 2 distinct return values when its parameters are permuted and we can call these two values s1, s2 and we know that s1 = -s2
(2) So, it follows that the two cases gives us two possible expressions:
(p + p1s1)(1/m) + (p - p1s1)(1/m)
and
(p + p1s2)(1/m) + (p - p1s2)(-1/m)
(3) But, clearly:
(p + p1s1)(1/m) + (p - p1s1)(1/m) =(p + [-p1s2])(1/m) + (p - [-p1s2])(1/m) =
= (p - p1s2)(1/m) + (p + p1s2)(1/m)
(4) So, it follows that swapping s1 and s2 does not change the value, so the number of return values when the m parameters are permuted is m.
QED
Theorem 2: A solution to the general quintic equation is not expressible by radicals.
Proof:
(1) Assume that a solution to the general quintic equation can be expressed in radicals. That is we can state an equation for each root y in terms of a,b,c,d,e such that:
y5 - ay4 + by3 - cy2 + dy - e = 0
(2) If a solution to this equation exists, it can be represented as follows (see Theorem 5, here):

where m is a prime number and R, p2, ..., pm-1 are all functions of this same form finitely nested at the deepest level each p,pi,R is a function of the coefficients of the general quintic equation.
(3) Using this form [see Theorem 5, here], we further note that the distinct roots of the quintic equation are expressible in terms of R:
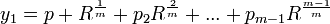

...
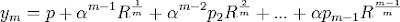
where α is an mth primitive root of unity [See here for a review of primitive roots of unity if needed]
(4) The Fundamental Theorem of Algebra gives us that the quintic equation has 5 roots. [See here for proof of the Fundamental Theorem of Algebra]
(5) Since this is the general solution, we can assume that each of the roots are distinct and that therefore, at the top level, m = 5.
(6) We can also state R(1/5) in terms of the roots (this was the gap that Ruffini assumed but did not prove). Using Corollary 5.1 here, we note that:
R(1/5) = (1/5)(y1 + α4y2 + ... + αy5)
(7) Now, by our result in step #2, we can assume that this same equation holds true at all levels. So at the lowest levels, we can assume that R is a rational function of the coefficients a,b,c,d,e.
(8) We can also show that at the bottom level, R is a function of the 5 roots. [See Corollary 3.1, here]
(9) Then, from step #7 and step #8, using Corollary 6.1, here, we can conclude that at the depeest level, m = 2.
(10) Now, we have two states to consider. Either the expression in step #2 consists of only two levels (at the top level m=5 and at the bottom level m=2) or its consists of more than two levels.
(11) So, if there exists a level above the lowest level but below the top level, then by step #2 above, it must be characterized by a prime m and by step #8 above we can assume that it is a function of the 5 roots.
(12) From Lagrange's Theorem (See Theorem, here), we can assume that if we permuted the 5 roots, the number of return values will divide 5! = 120.
(13) From Corollary 1.1, here and step #9 above, we know that the number of return values will be 2*m. Since 2*m must divide 120 and m must be a prime, we conclude that m=2, 3, or 5.
(14) But m ≠ 5, since from the reasoning of Corollary 1.1 in step #13, if m=5, then ultimately we would have 2*5*5*n return values which does not divide 120.
(15) We also know that m ≠ 2 since this gives us 2*2=4 return values and by Cauchy's Theorem (see Theorem 2, here), if the return values are less than 5, then it is 1 or 2.
(16) Further, we know that m ≠ 3 since:
(a) Let r = (p + p1S(1/2))(1/m)
where p,p1,S are symmetric with respect to the 5 roots of a quintic equation.
(b) Let r1 = (p - p1S(1/2))(1/m)
(c) So, we define a function on the 5 roots of the quintic equation such that:
f(y1, ..., y5) = r + r1
(d) From Lemma 1 above, such a function will return m distinct values when its m parameters are permuted.
(e) But, by Cauchy's Thereom used in step #15 above, if m is less than 5, it can only be 1 or 2.
(k) Hence, this means m ≠ 3.
(17) But, then it follows from steps #13, #14, #15, #16 above that the solution to the general quintic equation has only two levels and therefore the solution has the following form:

where m=5 and p,R,p2, ... p4 are functions of the form s + s1T(1/2) where s, T, s1 are rational functions of the coefficients of the quintic equation: a,b,c,d,e.
(18) Now, from step #6 above, we have:
R(1/5) = (1/5)(y1 + α4y2 + ... + αy5)
where α is a primitive 5th root of unity and y1, ..., y5 are the 5 distinct roots of a quintic equation.
(19) Now, from #17 above, we have:
R(1/5) = (s + s1T(1/2))(1/5)
where s, s1, T are symmetric on y1, ..., y5
(20) So, putting these two steps together gives us:
(1/5)(y1 + α4y2 + ... + αy5) = (s + s1T(1/2))(1/5)
(21) But this is clearly impossible since (1/5)(y1 + α4y2 + ... + αy5) can take 5!=120 distinct return values when its the parameters are permuted and (s + s1T(1/2))(1/5) can only take 2*5=10 distinct return values.
(22) Therefore, we have a contradiction and we reject our assumption in step #1.
QED
Corollary 2.1: A solution to the general n-th equation where n ≥ 6 is not expressible by radicals.
Proof
(1) Assume that a solution to a general n-th equation where n ≥ 6 is expressible by radicals.
(2) Let:
y5 - ay4 + by3 - cy2 + dy - e = 0
be a general quintic equation.
(3) Let i = n - 5 so that i ≥ 1.
(4) If we multiply (y - c1)*...*(y - ci)*(y5 - ay4 + by3 - cy2 + dy - e ), then we have an n-th equation.
(5) By assumption, we now solve this n-th equation so that our roots are y1, ..., y5, y6, ..., yn
(6) But then we have also solved the quintic equation using radicals which by Theorem 1 above is impossible.
(7) So, we have a contradiction and we reject our assumption in step #1.
QED
References
- Peter Pesic, Abel's Proof: An Essay on the Sources and Meaning of Mathematical Unsolvability, Appendix B, The MIT Press, 2004
- William Rowan Hamilton, "On the Argument of Abel", Transactions of the Royal Irish Academy, 18 (1839), pp 171-259.

11 comments:
May I say how impressed I am by your presentation.
I speak as someone whose math theory is rusty - very, very rusty.
So all the help and stepping stones you offer are invaluable.
Even so, sometimes my slowness and misunderstandings can still wreck my progress!
I've got to Step 13, your Wed 1st Oct 2008 post, and clicked on 'here' to find Corollary 1.1 (it doesn't appear to be on the given page)
But there was no link!
Can you possibly help me by telling me which blog post date Corollary 1.1 falls under?
With great gratefulness,
Dr. Ian MacIntyre (retd) at n_mcntyr@yahoo.co.uk
Hi Dr. MacIntyre,
Thanks very much for the feedback on my blog.
I've added the link to Corollary 1.1. Thanks very much for reporting this issue.
Cheers,
-Larry
Can anyone determine the margin of error of x1=-( 70038238698/60000000000) as one of the roots of x^5-x+1=0? Samuel Bonaya Buya
Again what would the margin of error in taking x=-(6822150561/5000000000) as the root of x^5-2x+2=0? Samuel Bonaya Buya
consider the quintic equation x^5-x+1=0. It can be factorized to
[x^2+x+2/(1+i√3)]
[x^3-x^2+(3-i√3)/(1+i√3) x+(1+i√3)/2]=0. This means it is a reducible quintic and it has radical solution. Similarly all other quintics can be reduced to auxiliary cubic and quadratic factors. This disproves Abel impossibility theorem.
Samuel Bonaya Buya
consider the quintic equation x^5-x+1=0. It can be factorized to
[x^2+x+2/(1+i√3)]
[x^3-x^2+(3-i√3)/(1+i√3) x+(1+i√3)/2]=0. This means it is a reducible quintic and it has radical solution. Similarly all other quintics can be reduced to auxiliary cubic and quadratic factors. This disproves Abel impossibility theorem.
Samuel Bonaya Buya
The note by Buya is incorrect. The product of the two factors gives a nonzero x^3 term when multiplied out. Another way to show that the quintic does not factor as shown is to substitute a value for x into both equations. For example, with x=3 we get 241 for the quintic, but 227.5-70.1i for the product of the quadratic and cubic terms.
E.T. Bell tells the story of how so many people were submitting papers on quintics alleging proof or disproof of their solvability, that Gauss trashed Abel's self-printed proof when he sent it to him as "another one of those monstrosities". It fell to Crelle and his new journal to give Abel his due, which turned out to make both of them famous.
Since that time almost 200 years ago, Abel's theorem has been validated by so many people, and so many alternative proofs have been presented of it from different angles, that it seems impossible that it could be disproven now.
Many thanks to Larry and his blog. I don't know how I could have worked through Dorrie's version of the theorem (third listed reference on the home page) without it (it requires more blog entries than just the current page).
I think Theorem 2 - (2) needs some additional punctuation.
Perhaps the phrase: " where m is a prime number and R,p1,p2.. .are functions of this same form finitely nested at the deepest level each p,pi,R is a function of the coefficients of the general quintic equation." needs to begin a new sentence after "level".
Also we can include "p" in the list "R, p1, p2".
Can we discuss Abel's impossibility proof with references to the findings in the links below?
https://www.google.com/url?sa=t&rct=j&q=&esrc=s&source=web&cd=3&cad=rja&uact=8&ved=0ahUKEwjmhfD1-svVAhVrJ8AKHTKSD4UQFgg0MAI&url=https%3A%2F%2Fwww.rroij.com%2Fopen-access%2Fthe-bringjerrard-quintic-equation-its-algebraic-solution-byconversion-to-solvable-factorized-form-.php%3Faid%3D86068&usg=AFQjCNF5ysB5wjKJjpnK4GJ4nOC-gg2NLA
Post a Comment