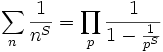Euler Product Formula

One of the major breakthroughs in Analytic Number Theory came with Leonhard Euler's Product Formula (see Theorem 4 below). Associated with this result is the Riemann zeta function which is the foundation of perhaps the most important unsolved mathematical problem in number theory today, the Riemann Hypothesis.

One might ask if Leonhard Euler came up with the zeta function why is it commonly called the Riemann Zeta Function. The answer has to do with the development of the function. While it is true that Euler discovered it, he used it with integer values. Johann Dirichlet would later extend it to real numbers, and Bernhard Riemann extended it to complex numbers. The most interesting properties stem from the complex numbers so it makes sense that it is currently named the Riemann zeta function (see Ed Sandifer's article for details).

So, how did Euler come up with the Euler Product Formula? The Harmonic Series was shown to be divergent (have an infinite sum) by Nicolas Oresme in the 1300s (this is considered one of the high points of mathematics in the middle ages, see Lemma 3 below). Euler wondered if the prime harmonic series (1 + 1/2 + 1/3 + 1/5 + ...) was also divergent. He then began studying the zeta function ζ(s) where:

ζ(s) = 1 + (1/2^s) + (1/3^s) + ...

For Euler, s is an integer. It turns out that when s=1, ζ(s) = the harmonic series and is therefore divergent. When s ≠ 1, it turns out the the zeta function is convergent, that is, it has a finite limit. In this way, Euler came up with his Product Formula. He then used this result to show that there are an infinitude of primes and the prime harmonic series is infinite. Unfortunately, while his conclusion about the prime harmonic series is correct, his proof today is not considered valid (see Ed Sandier's article for more information). See here for details on the proof for the divergence of the prime harmonic series.

Lemma 1: Infinite Geometric Series

if x ≠ 1, then:

1/(1-x) = 1 + x + x² + x³ + ... + xⁿ

Proof:

(1) Let s = 1 + x + x² + x³ + ... + xⁿ

(2) xs = x + x² + x³ + ... + xⁿ

(3) s - xs = 1

(4) s(1 - x) = 1

(5) s = 1/(1-x)

QED

Lemma 2: [1/(2ⁿ+1)] + ... + [1/(2ⁿ + 1 + 2ⁿ - 1)] ≥ (1/2)

Proof:

(1) At each n, we have a set of 2ⁿ elements.

For example, when n=0, we have 1 element (1/2)

When n=1, we have 2 elements (1/3, 1/4)

When n=2, we have 4 elements (1/5, 1/6, 1/7, 1/8) and so on.

(2) If we pair up two lists of elements in reverse order:

[1/(2ⁿ + 1)], [1/(2ⁿ+2)], ..., [1/(2ⁿ+1+2ⁿ-1)]
[1/(2ⁿ+1+2ⁿ-1)], [1/(2ⁿ+1+2ⁿ-2), ..., [1/(2ⁿ + 1)]

We can see that we have 2ⁿ columns where each pair adds up to [1/(2ⁿ + 1) + 1/(2ⁿ⁺¹) ]

(3) This means that sum of the series of [1/(2ⁿ + 1)] thru [1/(2ⁿ⁺¹)] is:

(1/2)(2ⁿ)[1/(2ⁿ + 1) + 1/(2ⁿ⁺¹)] =

= 2^n-1(2ⁿ⁺¹ + 2ⁿ + 1)/[(2ⁿ⁺¹)(2ⁿ + 1)] =

= (2ⁿ⁺¹ + 2ⁿ + 1)/[(2²)(2ⁿ + 1)]

(4) Now (1/2) = [(2)(2ⁿ + 1)]/[(2²)(2ⁿ + 1)]

(5) So, this lemma is proven since (2ⁿ + 1) ≥ 2 → (2ⁿ⁺¹ + 2ⁿ + 1) ≥ (2ⁿ⁺¹ + 2).

QED

Lemma 3: Harmonic Series Diverges

Let H = 1 + 1/2 + 1/3 + 1/4 + 1/5 + ... + 1/n

Then H has no limit and proceeds toward infinity

Proof:

(1) It is clear that the following sum S diverges and proceeds toward infinity:

S = 1 + 1/2 + 1/2 + 1/2 + ...

(2) Let H₁, H₂, etc. describe the elements that make up H. (So, that H₁ = 1, H₂ = 1/2, etc.)

(3) At each each point 2ⁿ+1, it is possible to group the elements into:

1/(2ⁿ + 1), 1/(2ⁿ+2), ..., 1/(2ⁿ+1+2ⁿ-1)

So that we have:

At [1/(2⁰ + 1)], we have: 1/2

At [1/(2¹ + 1)], we have: 1/3, 1/4

At [1/(2² + 1)], we have: 1/5, 1/6, 1/7, 1/8

and so on.

(4) Then using Lemma 2 above, we can be sure that the sum of each of these partitions is greater or equal to (1/2)

(5) This gives us that the sum of H ≥ sum of S.

QED

Theorem 4: Euler Product Formula





Proof:

(1) 1/(1-x) = 1 + x² + x³ + ... xⁿ [See Lemma 1 above]

(2) We can see that (1-x)^-1 = 1 + x² + x³ + ... xⁿ

(3) Let x = (1/p^s) where p is a prime.

(4) Then we have: (1 - 1/p^s)^-1 = 1 + 1/p^s + 1/p^2s + ... + 1/p^ns

(5) And, ∏(p) [(1 - 1/p^s)^-1] = ∏(p)[1 + 1/p^s + 1/p^2s + ... + 1/p^ns]

where ∏(p) is multiplication of the primes p.

(6) ∏(p)[1 + 1/p^s + 1/p^2s + ... + 1/p^ns] =

(1 + 1/2^s + 1/2^2s + ... + 1/2^ns)(1 + 1/3^s + 1/3^2s + ... + 1/3^ns)(1 + 1/5^s + 1/5^2s + ... + 1/5^ns)*...*(1 + 1/p^s + 1/p^2s + ... + 1/p^ns) =

= (1*1*1*...*1) + ([1/2^s]*1*1*...*1) + (1*[1/3^s]*1*...*1) + ([1/2^2s]*1*1*...*1) + (1*1*[1/5^s]*...*1) + ... + ([1/2^ns]*[1/3^ns]*[1/5^ns]*...*[1/p^ns]) =

= 1 + 1/2^s + 1/3^s + 1/4^s + 1/5^s + ... + 1/(2^ns*3^ns*5ns*...*p^ns) [By the Fundamental Theorem of Arithmetic]

= ∑(1,∞)n^s

QED

Corollary 4.1: There are an infinitude of primes

Proof:

(1) Assume that there are a finite number of primes.

(2) Then there exists an integer p such that p = the maximum prime.

(3) Then, ∏(1,p) [1/(1 - 1/p)] is finite number.

(4) But if s=1, then ∏(1,p) [1/(1 - 1/p)] = ∑(1,∞) 1/n. [See Theorem 4 above]

(5) Now, ∑(1,∞) 1/n is the Harmonic Series which diverges (that is, goes to infinity). [See Lemma 3 above]

(6) Therefore, we have a contradiction and we reject our assumption in step #1.

QED

References

• Ed Sandifer, How Euler Did It?, Mathematical Association of America Online, March, 2006
• Keith Devlin, The Millenium Problems, Basic Books, 2002
  
• Riemann Hypothesis, Wikipedia
• Riemann Zeta Function, Wikipedia
• Euler Product, Wikipedia
  

Regular Primes: Next Steps

Ernst Kummer presented his proof that Fermat's Last Theorem is true for regular primes in April of 1847. This is a brilliant proof that introduced the idea of ideal numbers and was the biggest advance in Fermat's Last Theorem up to that point.

Still, there were many questions that were raised: how does one determine the class number for a set of cyclotomic integers that are not characterized by unique factorization? How does one determine when Condition (B) applies for a set of cyclotomic integers. Do irregular primes exist?

Kummer announced that Johann Dirichlet had already found a formula for the class number and would show Dirichlet's work could be applied to the class number for cyclotomic integers. Kummer would later prove that Condition (A) implies Condition (B). Interestingly, out of this, would come a connection between class number and Bernoulli numbers (a prime is regular if it does not divide any of the Bernoulli numbers). Irregular primes do exist and it would later be proved that there are an infinite number of them.

All of this work was done between May and September of 1847. Harold M. Edwards has called this a "an extraordinary tour de force." (Harold M. Edwards, Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory) There turn out to be only 3 irregular primes less than 100, they are: 37, 59, and 67 so Kummer's proof was later used to show that Fermat's Last Theorem is true for integers less than 100. Using techniques from this proof, in 1993, Fermat's Last Theorem was proved to be true for all integers less than 4,000,000. (Of course, all these techniques were superceded when Andrew Wiles presented the first version of his famous proof on June 23, 1993.)

To dive into the advances made with regard to regular primes, it is first necessary to review the Euler Product Formula and show how this formula lead's to Dirichlet's formula for class number. I will show that if a prime does not divide its class number, then this shows that a prime is regular (in other words, using the definition of regular primes, Condition (A) implies Condition (B)) and finally, I will show that 37 is an irregular prime.

Ideal Numbers: Regular Primes

Today's blog continues the discussion on Ernst Kummer's Theory of Ideal Numbers and his proof of Fermat's Last Theorem for Regular Primes. For historical context, start here.

Today's content is taken straight from Harold M. Edwards Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory.

For standard integers, when we have:

uv = w^λ

If gcd(u,v)=1, then we know that u,v are both λth powers. (see Theorem, here)

When it comes to cyclotomic integers, unfortunately, this proof does not hold because to use unique factorization, we have to go through ideal numbers. Today's blog is about the method used by Kummer to apply this reasoning to ideal numbers.

For example, we know that if U is a principal divisor for u and V is a principal divisor for v, and gcd(U,V)=I, then U,V are λth; powers. That is, there exists C,D such that:

U = C^λ, V = D^λ where C,D are ideal numbers.

Lemma 1: gcd(U,V)=I and u(α)v(α)=w(α)ⁿ, then there exists C,D such that U=Cⁿ, V=Dⁿ

Proof:

(1) So, we start with gcd(U,V) = I, UV = Wⁿ [We know this since principal divisors have the same relations as their corresponding cyclotomic integers, see here]

(2) Assume that U is not equal to any ideal number Xⁿ

(3) U ≠ I since I is an Xⁿ power [Since Iⁿ = I]

(4) Now, U is divisible by a prime divisor P. [See Definition 3, here]

(5) So, there exists K such that U = PK

(6) P divides W since Wⁿ = UV = PKV [By applying Euclid's Lemma for Prime Divisors]

(7) So, there exists M such that W=PM

(8) So, Wⁿ = UV = PKV = (PM)ⁿ = PⁿMⁿ

(9) Dividing P from both sides gives us:

KV = P^(n-1)Mⁿ

(10) From Euclid's Lemma, P divides K or V.

(11) It can't divide V since it already divides U and gcd(U,V)=I. Therefore, it divides K

(12) We can apply this same argument for each P in P^(n-1)

(13) So, we can conclude that P^(n-1) divides K.

(14) So, there exists Z such that K = p^(n-1)*Z

(15) So, KV = P^(n-1)Mⁿ = P^(n-1)*Z*V

(16) Dividing p^(n-1) from both sides gives us:

ZV = Mⁿ

(17) Now, gcd(Z,V)=1 since Z is a divisor of U and gcd(U,V) = I

(18) Likewise, Z cannot be an n-power. If it were, then U = pⁿZ would make U an n-power which goes against our assumption in step #2.

(19) Finally, N(Z) is less than N(U) since N(P^(n-1)) > 1.

(20) Thus, we have a contradiction by infinite descent.

QED

In order to prove that u,v are both λth powers we need to show that C,D are principal.

This then is the problem that Kummer addressed, under what circumstances can we assume that U = C^λ where U is principal imply that C is also principal.

To help with this question, let's consider an important insight.

Theorem 2: For any ideal number C, if h is the class number, then C^h ~ I

In other words, C^h is principal.

Proof:

(1) Let h be the class number for the cyclotomic integers corresponding to λ

(2) Based on the theorem regarding class numbers (see Theorem, here), we know that all ideal numbers are equivalent to one of the ideal numbers of a representative set: A₁, A₂, ..., A_h

(3) This means that each of the ideal numbers C, C², C³, etc. are equivalent to an ideal number A_i

(4) Since there are only h such ideal numbers in the representative set, eventually, there are two ideal numbers C^j and C^j+k that are equivalent to the same A_i and therefore equivalent to each other.

(5) For each ideal number, there exists another ideal number B such that:

C^jB is principal [See Lemma 6, here]

(6) Because C^j ~ C^j+k:

C^j+kB is also principal.

(7) But C^j+kB is principal and C^jB is principal, then C^k is also principal. (See Lemma 2, here)

(8) Let d be the first power of C that is principal.

So that we have:

C^d ~ I

C, C², ..., C^d-1 are inequivalent to each other and not principal.

If any of these were equivalent to each other, then there would a power less than d which is principal which goes against our definition of d.

(9) Since I,C, C², ..., C^d-1 are all inequivalent, then we know that they correspond to d of the A_i which make up the representative set of ideal numbers.

(10) If this exhausts all the elements of the represenative set then d=h so to complete this proof, we only need to consider the situation where d is less than h.

(11) If d is less than h, then there is an ideal number A_i that is not equivalent to any of the powers I,C,C², ..., C^d-1. Let's call it E.

(12) Then E, EC, EC², ..., EC^d-1 give d more ideal numbers that are inequivalent to each other and inequivalent to the first set of d ideal numbers (in step #11).

(a) Assume ECⁱ ~ EC^j where i ≠ j and both i,j are positive integers less than d.

(b) So that we have ECⁱ ~ EC^i+k where i+k=j.

(c) Then we have a C^k that is principal where k is less than d which is impossible so we reject our assumption.

(d) Assume E ~ ECⁱ where i is less than d.

(e) Then we have C_i is principal which again is impossible.

(f) Assume ECⁱ ~ C^j

(g) If j ≥ i, then this gives us that E is principal which goes against our assumption step #11 so we can reject this.

(h) If j is less than i, then we have:

EC^j+k ~ C^j

This gives us that C_j is principal which goes against our assumption since j is less than d.

(i) So, steps (a) thru (h) prove that this new set E, EC, EC², ..., EC^d-1 is inequivalent to each other and to the powers of Cⁱ.

(13) This either exhausts all A_i of the representative set or we can do the same thing until we are done. At the end, we are left with a disjoint set of d elements each.

(14) This gives us that d divides h so that C^d ~ I → C^h ~ I.

QED

Using the Theorem above, it is now possible to state under what conditions C^λ is principal implies that C is principal.

Corollary 2.1: If C^λ ~ I and λ doesn't divide the class number h, then C ~ I

Proof:

(1) Because λ is prime, if h is not divisible by λ, then there exists m,n such that mh = nλ + 1. [See Lemma 1, here for proof]

(2) I ~ C^h (from Theorem 1 above) so I ~ (C^h)^m (see Lemma 1, here)

(3) (C^h)^m = C^hm = C^nλ+1 = (C^λ)ⁿC

(4) From the given we know that (C^λ) ~ I so we also know that (C^λ)ⁿ ~ I.

(5) But I*C = C so (C^λ)ⁿC ~ I*C ~ C

(6) Since I ~ (C^nλ+1) and (C^nλ+1)~C, it follows that C ~ I and therefore, that C is principal.

QED

So, the corollary gives us the justification for considering the situation where λ doesn't divide the class number. This is Kummer's condition (A).

(A) The exponent λ has the property that it does not divide the corresponding class number.

Let's return now to the original problem. Let's say we have:

uv = w^λ

where gcd(u,v)=1 and λ does not divide the corresponding class number.

In this case we have that there exists C,D such that C^λ = U, D^λ=V and both C,D are principal.

This gives us that there exists cyclotomic integers c,d such that:

u = ec^λ
v = e'd^λ

where e,e' are cyclotomic units.

This did not satisfy Kummer. He wanted to find the condition where we could conclude that:

u = c^λ
v = d^λ

This leads us to condition (B)

(B) The exponent λ should have the property that a unit e in the set of corresponding cyclotomic integers has the following property:

e ≡ integer (mod λ) if and only if there exists a unit e' such that e = (e')^λ

To show the value of this. let's consider a second theorem.

Lemma 3: (a₀ + a₁ + ... + a_λ-1)^λ ≡ a₀^λ + a₁^λ + ... + a_λ-1^λ (mod λ)

(1) (a + b)^λ ≡ a^λ + b^λ (mod λ) (See Lemma 1, here)

(2) (a + c + d)^λ ≡ (a + (c+d))^λ ≡ a^λ + (c+d)^λ (mod λ)

(3) Since (c + d)^λ ≡ c^λ + d^λ (mod λ)

(4) So that we have (a + c + d)^λ ≡ a^λ + (c+d)^λ ≡ a^λ + c^λ + d^λ ≡ (mod λ)

(5) Using the same logic we can show that:

(a + b + c + d + ...)^λ = (a + (b + (c + (d + ...)))^λ ≡ a^λ + b^λ + c^λ + ... (mod λ)

QED

Corollary 3.1: if g(α) is a cyclotomic integer then g(α)^λ ≡ integer (mod λ)

Proof:

(1) Because g(α) is a cyclotomic integer, we have:

g(α) = a₀ + a₁α + ... + a_λ-1α^λ-1 [See Lemma 1, here]

(g(α))^λ = (a₀ + a₁α + ... + a_λ-1α^λ-1)^λ ≡ (a₀)^λ + (a₁α)^λ + ... + (a_λ-1α^λ-1)^λ (mod λ) [See Lemma 3 above]

(2) Since (αⁱ)^λ = (α^λ)ⁱ = 1ⁱ = 1, we have:

(g(α))^λ ≡ (a₀)^λ + (a₁)^λ + ... + (a_λ-1)^λ (mod λ) = integer

QED

Theorem 4: if a set of cyclotomic integers corresponding to an odd prime λ satisfies condition (A) and condition (B) and u ≡ integer (mod λ), then if uv=w^λ where gcd(u,v)=1, then u,v are λth powers.

Proof:

(1) From Corollary 2.1 above, we have:

u = ec^λ

(2) u ≡ ec^λ ≡ e*b (mod λ) for some integer b [See Corollary 3.1 above]

(3) So e ≡ integer (mod λ) since e ≡ u/b (mod λ) where b divides u and both b,u are congruent to integers mod (λ).

(4) So therefore (condition B), there exists e' such that e = (e')^λ

(5) Let c' = (e'c)

(6) Then we have: u= (c')^λ We can make the same argument for v so we are done.

QED

Definition 1: Regular Prime

A prime λ is a regular prime if λ and the corresponding cyclotomic integers satisfy the following two conditions:

(A) The exponent λ has the property that it does not divide the corresponding class number.

(B) The exponent λ should have the property that a unit e in the set of corresponding cyclotomic integers has the following property:

e ≡ integer (mod λ) if and only if there exists a unit e' such that e = (e')^λ

We can now use this definion to establish the following theorem:

Lemma 5: For a regular prime λ, if a corresponding cyclotomic integer g(α) has a divisor G which is a λth power and g(α) ≡ integer (mod λ), then there exists a cyclotomic integer h(α) such that g(α) = h(α)^λ

Proof:

(1) Since G is λth power, there exists a divisor H such that:

G = H^λ

(2) Since λ is regular (see Definition 1 above), we know that H is principal (see Corollary 1.1 above)

(3) Therefore, there exists h(α) such that H is the principal divisor for h(α) (see Definition 2, here for definition of a principal divisor)

(4) So we have g(α) = eh(α)^λ where e is a unit.

(5) Now, g(α) ≡ integer (mod λ) [from the given]

(6) Further, h(α)^λ ≡ integer (mod λ) [from Corollary 3.1 above]

(7) So, from this, we have: e ≡ integer/integer ≡ integer (mod λ) [since h(α) divides g(α) and both are congruent to integers mod (λ)

(8) So by Condition (B), there exists e' such that e = (e')^λ

(9) Let h'(α) = e'h(α)

(10) Then we have that g(α) = (h'(α))^λ

QED

Theorem 6: Criteria for a λth power

if g(α) ≡ nonzero (mod λ), then g(α) = h(α)^λ if and only if its divisor is a λth power and g(α) ≡ integer (mod λ)

if g(α) ≡ 0 (mod λ), then g(α) = h(α)^λ if and only if its divisor is a λth power and its quotient by the largest power of α - 1 is congruent mod λ to an integer.

Proof:

Case I: g(α) = h(α)^λ → ∃ G,H such that G = H^λ and g(α) ≡ integer (mod λ)

(1) Assume g(α) ≡ nonzero (mod λ)

(2) Assume g(α) = h(α)^λ

(3) Let G,H be divisors of g(α),h(α)

(4) We can see that G = H^λ so G is a λth power [See Theorem, here]

(5) We can also see that g(α) ≡ integer (mod λ) since h(α)^λ ≡ integer (mod λ) from Corollary 3. 1 above.

QED

Case II: G = H^λ and g(α) ≡ integer (mod λ) → ∃ h(α) such that g(α)=h(α)^λ

(1) This follows from Lemma 5 above.

QED

Case III: g(α) ≡ 0 (mod λ), g(α) = h(α)^λ → an ideal number G is a λth power and quotient by the largest power of α - 1 is congruent mod λ to an integer

(1) Assume g(α) = h(α)^λ

(2) Let G,H be the divisor of g(α),h(α)

(3) G = H^λ so we that its divisor G is a λth power. [See Theorem, here]

(4) Since g(α) is divisible by λ, it is divisible by (α-1) since (α-1)^λ-1 = λ (see Corollary 3.2, here) so that we have:

g(α) = (α-1)^kg'(α) where g'(α) is not divisible by (α - 1) and k ≥ 1.

(5) Since α - 1 is a prime divisor and since g(α) is a λth power, λ must divide k so that we have:

g(α) = [(α-1)^k/λ]^λg'(α)

(6) By the same argument, the powers of the prime divisors that divide g'(α) must also be divisible by λ so that there exists an ideal number H' such that:

G' = (H')^λ

(7) Since G' = (H')^λ is principal, then H' must also be principal so that there exists h'(α) such that:

g'(α) = eh'(α)^λ where e is a unit.

But since h(α)^λ = [(α-1)^k/λ]^λg'(α), it follows that e must also be a λth power.

(8) But the only way this is possible by Condition B is if e ≡ integer (mod λ)

(9) Therefore, we have g(α) ≡ e * h(α)^λ ≡ integer * integer (mod λ)

QED

Case IV: if its divisor G is a λth power and its quotient by the largest power of α - 1 is congruent mod λ to an integer → g(α)=h(α)^λ

(1) So there exists an ideal number H such that G = H^λ

(2) g(α) = (α-1)^k*g'(α)

(3) So g'(α) ≡ integer (mod λ)

(4) H is principal from Corollary 2.1 above so there exists h(α) such that g(α) = eh(α)^λ

(5) Let G' be the principal divisor for g'(α)

(6) Since G is a λth power, all the powers of the prime divisors that make up G must be divisible by λ.

(7) If G' is all the prime divisors minus (α - 1), G' must also be a λth power so that there exists H' such that G' = (H')^λ

(6) Since G' = (H')^λ is principal, H' is principal (See Corollary 2.1 above)

(7) So there exists h'(α) such that g'(α) ≡ eh'(α)^λ

(8) Now g'(α) ≡ integer (mod λ) [from given] and h'(α)^λ ≡ integer (mod λ) [from Corollary 3.1 above) so that e ≡ integer (mod λ)

(9) Now using Condition B, this gives us that there exists e' such that e = e'^λ

(10) This then gives us that g'(α) = [e'h'(α)]^λ

(11) This also gives us that g(α) = [(α-1)^k/λe'h'(α)]^λ

QED

Kummer made three conjectures regarding regular primes:

(1) There exist irregular primes that do not satisfy conditions (A) and (B). [Proof that 37 is irregular will be proved later]

(2) Condition (A) implies Condition (B). [Proof of this will be presented later]

(3) Regular primes are infinite in number.

This last conjecture is still an open question. There has a been proof that there are infinite irregular primes but no one has proven that there are infinite regular primes. Kummer was able to prove the first two conjectures within a few months after the stated them. The third conjecture he later retracted saying that he didn't know.

Kummer's Proof for Regular Primes: Case II

In today's blog, I continue the proof of Fermat's Last Theorem for regular primes. Case II makes the assumption that λ divides z and that each of the factors (x + αⁱy) are divisible by α - 1 and the resulting quotients are relatively prime. For context and definitions, please start here at the beginning of this proof.

The details of today's content is taken from Harold M. Edwards Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory.

Lemma 1: (1 + α) is a unit

Proof:

(1) (α² - 1) = (α - 1)*(α + 1)

(2) Since (α² - 1) is a cyclotomic integer of the form (α^j - 1), this proves that (α + 1) is a unit. [See Lemma 3, here]

QED

Lemma 2: αⁱ is a unit

Proof:

(1) α^λ = 1 is a unit. [See Definition 1, here for definition of cyclotomic unit]

(2) αⁱ divides α^λ so therefore αⁱ is a unit. [See Lemma 5, here]

QED

Theorem: Case II of Kummer's Proof for Regular Primes

If λ divides z, (α - 1) divides all (x + αⁱy), and the resulting quotients are all relatively prime, then:

if x^λ + y^λ = z^λ where x,y,z are integers then xyz=0.

Proof:

(1) From the main proof (see here), we know that:

z^λ = x^λ + y^λ = (x + y)(x + αy)(x + α²y)*...*(x + α^λ-1y).

and we assume xyz ≠ 0.

(2) By the given, we know that each x + α^jy is divisible by α - 1, so that we have:

z^λ(α-1)^-λ = each factor divided by α - 1.

(3) Since the factors that make up z^λ(α-1)^-λ are pairwise relatively prime, it follows that the divisor of each factor is a λth power. (See Lemma 1, here)

(4) Using a property of divisors (see Corollary, here), for each x + α^jy, we have:

(α-1)^-1(x + α^jy) = e_j(t_j)^λ

where e_j is a cyclotomic unit and t_j is a cyclotomic integer.

(5) Since each factor divided by (α - 1) is relatively prime to the others, we can conclude that each t_j is relatively prime to the t_i.

(6) From #4, we know that (α - 1) can only divide one t_i and in fact, it divides t₀ since:

(a) x,y are rational integers

(b) (α - 1) divides λ so α - 1 divides x+y implies that (α-1)^λ-1 divides x + y.

This is true since (x + y) is a rational integer and the only way α - 1 can divide a rational integer is if λ=(α-1)^λ-1 (see Corollary 3.2, here) divides (x + y).

(7) Since (α-1) divides t₀, there exists k,w such that:

t₀ = (α-1)^kw where k ≥ 1 and w is not divisible by (α - 1). [In fact, we know that k is at least λ-2]

(8) We now have the following equations:

(a) x + α^-1y = (α - 1)e_-1(t_-1)^λ

The equation in step #4 gives us:

(α-1)^-1(x + α^λ-1y) = e_λ-1(t_λ-1)^λ

Multiplying (α-1) to both sides gives us:

x + α^λ-1y = (α-1)e_λ-1(t_λ-1)^λ

Since α^λ-1 = α^-1, we can also represent this as :

x + α^-1y = (α-1)e_-1(t_-1)^λ

(b) x + y = (α-1)e₀(α-1)^kλw^λ

The equation in step #4 gives us:

(α-1)^-1(x + y) = e₀(t₀)^λ

Multiplying (α-1) to both sides gives us:

x + y = (α-1)e₀(t₀)^λ

Applying step #7 gives us:

x + y = (α -1)e₀(α-1)^kλw^λ

(c) x + αy = (α-1)e₁(t₁)^λ

The equation in step #4 gives us:

(α-1)^-1(x + αy) = e_λ1(t_λ1)^λ

Multiplying (α-1) to both sides gives us:

x + αy = (α-1)e₁(t₁)^λ

(9) (α - 1)y = (α - 1)[e₁(t₁)^λ - e₀(α - 1)^kλw^λ] since:

(x + αy) - (x + y) = αy - y = (α - 1)y =

= (α - 1)([e₁(t₁)^λ] - [e₀(α-1)^kλw^λ])

(10) (α - 1)y = (α - 1)[αe₀(α - 1)^kλw^λ - αe_-1(t_-1)^λ ] since:

(x + y) - (x + α^-1y) = y - α^-1y = α^-1(α - 1)y =

= (α - 1)[e₀(α - 1)^kλw^λ - (e_-1(t_-1)^λ]

Now if we multiply α to each side, we get:

(α - 1)y = (α - 1)[αe₀(α - 1)^kλw^λ - (αe_-1(t_-1)^λ]

(11) Now if we substract the result in #10 from the result in step #9 we get:

(α -1)y - (α - 1)y = 0 =

= (α - 1) [e₁(t₁)^λ - e₀(α - 1)^kλw^λ - αe₀(α - 1)^kλw^λ + αe_-1(t_-1)^λ]

Now if we divide (α - 1) from both sides we get:

0 = e₁(t₁)^λ - e₀(α - 1)^kλw^λ - αe₀(α - 1)^kλw^λ + αe_-1(t_-1)^λ

(12) Now, let's define E₀, E_-1 such that:

E₀ = [(α + 1)e₀]/e₁

E_-1 = (α*e_-1)/e₁

(13) We can see that both E₀ and E_-1 are units since:

(a) (α+1) is a unit [See Lemma 1 above]

(b) So (α + 1)*e₀ is a unit [See Lemma 3, here]

(c) So [(α + 1)e₀]/e₁ is a unit [See Lemma 5, here]

(d) (α) is a unit [See Lemma 2 above]

(e) So α*e_-1 is a unit [See Lemma 3, here]

(f) So (α*e_-1)/e₁ is a unit [See Lemma 5, here]

(14) We can use E₀, E_-1 to simplify the equation in step #11

0 = e₁(t₁)^λ - e₀(α - 1)^kλw^λ - αe₀(α - 1)^kλw^λ + αe_-1(t_-1)^λ = e₁(t₁)^λ -(e₀ + αe₀)(α - 1)^kλw^λ + αe_-1(t_-1)^λ = e₁(t₁)^λ -(e₀)(1 + α) (α - 1)^kλw^λ + αe_-1(t_-1)^λ

Now, if we add (e₀)(1 + α) (α - 1)^kλw^λ to both sides we get:

(e₀)(1 + α) (α - 1)^kλw^λ = e₁(t₁)^λ + αe_-1(t_-1)^λ

Finally, if we divide e₁ from both sides, we get:

[(e₀)(1 + α)/e₁ ] (α - 1)^kλw^λ = (t₁)^λ + (αe_-1/e₁₎(t_-1)^λ =

= E₀(α - 1)^kλw^λ = (t₁)^λ + E_-1(t_-1)^λ

(15) Since (α-1)^λ-1 = λ * unit (see Corollary 3.2, here), we know that:

0 ≡ C₁ + E_-1C_-1 (mod λ) where C₁ ≡ (t₁)^λ (mod λ) and C_-1 ≡ (t_-1)^λ (mod λ) where C₁ and C_-1 are integers [See Corollary 3.1, here]

(16) C₁, C_-1 are not zero mod λ, since they are relatively prime to t₀ which is divisible by λ. [see step #5 above]

(17) Thus, E_-1 ≡ integer (mod λ) [This follows from step#15 and step#16]

(18) Finally, we can conclude that E_-1 = e^λ for some unit e. [This follows from Condition (B) in the definition of regular primes, see here]

(19) Let a = t₁; Let b = et_-1.

(20) Now applying step #14 to step#19 gives us:

a^λ + b^λ = E₀(α - 1)^kλw^λ

where E₀ is a unit, k is a positive integer, and a,b,(α - 1),w are pairwise relatively prime cyclotomic integers.

(21) E₀(α - 1)^kλw^λ = a^λ + b^λ = (a + b)(a + αb)(a + α²b)*...*(a + α^λ-1b) [See Lemma 1, here for details on this refactoring]

(22) By this equation is it clear that at least one of the factors (a+α^jb) is divisible by α - 1 and from this, it follows that all the factors are divisible by α - 1. [See Step #7 in main theorem, here for proof]

(23) It further follows that all the quotients are relatively prime. [See Step #6 in main theorem, here for proof]

(24) The previous argument (see step #5) that x + y is divisible by (α - 1)² no longer applies since a,b are not necessarily rational integers.

(25) But it is still true that at least one of the factors (a + α^jb) is divisible by (α - 1)² since:

(a) Using Lemma 3 here, we see that:

there exists integers c₀, c₁, d₀, d₁ such that:

a ≡ c₀ + c₁(α - 1) (mod (α - 1)²)

b ≡ d₀ + d₁(α - 1) (mod (α - 1)²)

(b) a + α^jb ≡ [c₀ + c₁(α - 1)] + [1 + (α - 1)]^j[d₀ + d₁(α - 1)] ≡

≡ c₀ + d₀ +[c₁ + d₁ + jd₀](α - 1) mod (α - 1)²

(c) Since (α - 1) divides all a + α^jb by step #22, we see that #25b implies that (α -1) divides c₀ + d₀ and further since c₀, d₀ are rational integers, this implies that λ divides c₀ + d₀.

(d) This also shows that:

(α - 1)² divides a + α^jb if and only if c₁ + d₁ + jd₀ ≡ 0 (mod λ).

This is true since (c₁ + d₁ + jd₀) is a rational integer and (α - 1) only divides a rational integer if λ divides that integer.

(e) This condition holds true for one and only value of j mod λ since (α - 1)² can only divide one since after division by (α - 1) all a + α^jb are relatively prime.

(f) This condition only holds true for one and only if one if d₀ ≡ nonzero (mod λ). The reason for this is that c₀ is shared by all a and if d₀ ≡ 0, then all a + α^jb values would be divisible by (α - 1)².

(g) Additionally, d₀ ≡ nonzero (mod λ) because otherwise (α - 1) would divide b (from step #25a) contrary to step #20 where we stated that a,b,w, and α -1 are relatively prime.

(26) From step #25, we can see that if (α - 1)² divides any factor of a + α^jb, then in the equation in step #21, k must be greater than 1.

(27) From this, we can assume that there exists a positive integer K such that k = K+1.

(28) Let B = α^jb where (α - 1)² divides a + α^jb in step #25.

This means then that we have the following equation:

a^λ + b^λ = (a + B)(a + αB)(a + α²B)*...*(a + α^λ-1B)

We can do this since if B = α^jb, then αB = α^j+1b, and further α^j-1b = α^λ-1B.

(29) Now, we note that of the (α - 1)^kλ that divide a^λ + b^λ, there are (α-1)^λ-1 that divide a + αⁱb where i ≠ j and (α-1)^{1 + Kλ} that divide a + B.

(30) Using the revised equation in step #28, we know that each factor is relatively prime so that it follows that the divisor of each factor is a λth power. (See Lemma 1, here)

(31) Using a property of divisors (see Corollary, here), for each a + α^jB, we have:

(α - 1)^-1(a + αⁱB) = e_i(t_i)^λ

(32) We can now follow the same reasoning in step #8 to get:

a + α^-1B = (α - 1)e_-1(t_-1)^λ

a + B = (α - 1)e₀(α - 1)^Kλw^λ

a + αB = (α - 1)e₁(t₁)^λ

(33) We can follow the same logic in steps #9 to #20 to get:

E(α - 1)^Kλw^λ = X^λ + Y^λ where X = t₁ and Y = et_-1.

We also note that:

X, Y, w, and (α - 1) are all pairwise relatively prime, E is a unit, and K = k-1.

(34) But this means that we are exactly in the same state as step #20 so that we can repeat this same process with a new integer K' = K-1 and so on ad infinitum with each time the positive integer K' decreasing by 1.

(35) Since K' is a positive integer, eventually we get to the state where K'=1 but this is impossible by step #26 where we saw that K' must be greater than 1.

(36) Therefore, we have an impossibility and the proof is done.

QED