In today's blog, I continue to review results from Harold Edward's Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory. I am continuing down the same chapter that I started in an earlier blog. If you would like to start at the beginning of cyclotomic integer properties, start here.
Lemma 1: g(α) = g(αp) if and only if g(α) is a cyclotomic integer made up of periods of length f.
Proof:
(1) Let λ be an odd prime.
(2) Let α be a primitive root of unity such that αλ = 1.
(3) Let p be an odd prime distinct from λ
(4) Let τ be mapping such that τα = αp
(5) Let f be the least positive integer for which pf ≡ 1 (mod λ)
(6) We know that f divides λ -1 since:
(a) pλ-1 ≡ 1 (mod λ) from Fermat's Little Theorem (since p,λ are distinct primes)
(b) From a previous result (see Lemma 2 here), we know if f is the least positive integer, then it must divide λ-1.
(7) Let e= (λ-1)/f
(8) Assume that g(α) is made up of periods of length f. [See here for review of cyclotomic periods]
(9) Then, σeg(α) = g(α) [See Lemma 4 here for details.]
(10) Then, there must exist an integer k such that:
τ = σk
Since the primitive root (see here for review if needed) can take all possible values mod λ [By definition σ = a mapping between α and αγ where γ is a primitive root, see here]
(11) Using step #10, we note that:
τf = σkf
Since τf ≡ 1 (mod λ), we know that σkf ≡ 1 (mod λ)
(12) Since the order of λ is λ -1 (see here), we know that kf must be divisible by λ - 1 (see Lemma 2 here) which means it is divisible by ef since ef=λ - 1.
So, ef divides kf means that e must divide k.
(13) So, from step #10 and step #12:
τ is a power of σe
(14) So, there exists k' such that ek' = k.
(15) From #14, we have:
τ = (σ1e)(σ2e)...(σk'e)
and therefore:
τg(α) =(σ1e)(σ2e)...(σk'e)g(α) = g(α)
(16) Assume that τg(α) = g(α)
(17) We know that there exists k such that:
τ = σk [Since σ is a mapping to γ which is a primitive root and the primitive root can take on all values modulo λ]
(18) Since g(α) repeats at τg(α), we know that g(α) consists of e periods of length f. [See Corollary 1.2 here]
(19) By definition, e divides (λ - 1) [See here for definition of periods]
(20) Thus, e is a common divisor of k and λ - 1.
(21) e is the greatest common divisor of k and λ - 1 since:
(a) Let d be an integer that divides both k, λ-1 so that:
k = qd
λ - 1 = df'
(b) Now,
τf' = σkf' = σqdf' = σ(λ - 1)q which is identity[from step #17, #21a, and since σλ-1 is the identity, see here]
(c) So that:
f' ≥ f [Since f is least value where pf ≡ 1 (mod λ)]
d ≤ e [Because d = (λ-1)/f' where f' ≥ f and e=(λ - 1)/f]
(22) Using Bezout's Identity, there exists a,b such that:
e = ak + b(λ - 1)
(23) Further,
σe = σakσb(λ-1) = [from step #22]
= σak = [Since σb(λ-1) is identity]
= τa [Since τ = σk from step #17]
(24) From this, we see that:
σeg(α) = τag(α) = g(α)
QED
Lemma 2: Let h(α) be a prime cyclotomic integer. For any cyclotomic integer g(α) made up of periods of length f, there exists an integer u such that g(α) ≡ u (mod h(α))
Proof:
(1) Fermat's Little Theorem gives us:
xp-1 ≡ 1 (mod p)
So that:
p divides xp-1 - 1
So that:
x(xp-1 - 1) = xp - x ≡ 0 (mod p)
(2) We also know that:
(x -1)*(x-2)*...(x-p) ≡ 0 (mod p)
(a) There exists a r such that x ≡ r (mod p)
(b) We know that p divides x - r
(c) We also know that r is between 0 and p-1.
(d) if r is 0, then p divides x-p; otherwise, p divides x-r.
(3) Putting (#1) and (#2) together, we have:
xp - x ≡ (x-1)(x-2)*...*(x-p) (mod p)
(4) Let x = g(α)
(5) Then:
g(α)p - g(α) ≡ [g(α) - 1][g(α) - 2]*...*[g(α) - p] (mod p)
(6) From a previous result (see Lemma 3 here), where g(α)p ≡ g(αp) (mod p), we have:
g(αp) - g(α) ≡ [g(α) - 1][g(α) - 2]*...*[g(α) - p] (mod p)
(7) Since h(α) divides p, then we have:
g(αp) - g(α) ≡ [g(α) - 1][g(α) - 2]*...*[g(α) - p] (mod h(α))
(8) Now, since g(α) is made up of periods of length f, we know that g(αp) = g(α) [See Lemma 1 above]
So that:
g(αp) - g(α) = 0 ≡ 0 (mod h(α))
(9) This gives:
[g(α) - 1][g(α) - 2][g(α) - 3]*...*[g(α)-p] ≡ 0 (mod h(α))
(10) Since h(α) is a prime cyclotomic integer, one of these values must be divisible by h(α) [By the definition of a cyclotomic prime, see here]
(11) So there exists an integer u such that h(α) divides g(α) - u
Which means that:
g(α) ≡ u (mod h(α))
QED
Corollary 2.1: Let h(α) be a prime cyclotomic integer. Let ηi be a period of length f. Then, there exists an integer ui such that ηi ≡ ui (mod h(α))
Proof:
(1) Each period ηi can be thought of as a cyclotomic integer made up of periods of length f:
g(α) = (0)η0 + ... + (1)ηi + ... + (0)ηe-1 = ηi
(2) From Lemma 2 above, we know that there exists an integer ui such that g(α) ≡ ui (mod h(α))
(3) So, we see that for each ηi, there exists ui such that:
ηi ≡ ui (mod h(α))
QED
Thursday, May 25, 2006
Cyclotomic Integers: g(α)p ≡ g(αp) (mod p)
In today's blog, I continue to review results from Harold Edward's Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory. I am continuing down the same chapter that I started in an earlier blog. If you would like to start at the beginning of cyclotomic integer properties, start here.
Lemma 1: if p is a prime, then (x + y)p ≡ xp + yp
Proof:
(1) Using the Binomial Theorem, we know that:
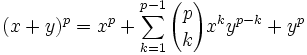
(2) Now, this means that each of the coefficients is equal to:
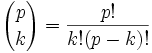
(3) But since p is a prime, p divides all coefficients.
For all values where k is between 1 and p-1, p, as a prime, will not be divisible by either k! or by (p-k)!.
(4) This means that p will divides (x + y)p - xp - yp.
QED
Lemma 2: xp ≡ x (mod p)
Proof:
(1) xp - x = x(xp-1 - 1)
(2) if gcd(x,p)=1, then by Fermat's Little Theorem, xp-1 ≡ 1 (mod p) so p divides xp-1-1.
(3) if p divides x, then of course p divides x(xp-1-1)
QED
Lemma 3: g(α) ≡ g(αp) mod p
Proof:
(1) Let g(α) = a0 + a1α + ... + αλ-1αλ-1.
(2) Then g(α)p = (a0 + [a1α + ... + αλ-1αλ-1])p
(3) Now using Lemma 1 above, we can break #2 out in the following ways:
(a0 + [a1α + ... + αλ-1αλ-1])p ≡ (a0)p + (a1α + [... + αλ-1αλ-1])p (mod p).
(4) We could keep breaking out each element until we get:
(a0 + [a1α + ... + αλ-1αλ-1])p ≡ (a0)p + (a1α)p + ... + (aλ-1αλ-1)p (mod p)
(5) Now for each coefficient ai, using Lemma 2 above, we have:
aip ≡ ai (mod p)
So this gives us:
(a0)p + (a1α)p + ... + (aλ-1αλ-1)p ≡ a0 + a1αp + ... + aλ-1(αλ-1)p (mod p)
(6) And we are done since this shows that:
g(α)p ≡ g(αp) (mod p)
QED
Lemma 1: if p is a prime, then (x + y)p ≡ xp + yp
Proof:
(1) Using the Binomial Theorem, we know that:
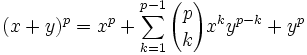
(2) Now, this means that each of the coefficients is equal to:
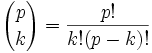
(3) But since p is a prime, p divides all coefficients.
For all values where k is between 1 and p-1, p, as a prime, will not be divisible by either k! or by (p-k)!.
(4) This means that p will divides (x + y)p - xp - yp.
QED
Lemma 2: xp ≡ x (mod p)
Proof:
(1) xp - x = x(xp-1 - 1)
(2) if gcd(x,p)=1, then by Fermat's Little Theorem, xp-1 ≡ 1 (mod p) so p divides xp-1-1.
(3) if p divides x, then of course p divides x(xp-1-1)
QED
Lemma 3: g(α) ≡ g(αp) mod p
Proof:
(1) Let g(α) = a0 + a1α + ... + αλ-1αλ-1.
(2) Then g(α)p = (a0 + [a1α + ... + αλ-1αλ-1])p
(3) Now using Lemma 1 above, we can break #2 out in the following ways:
(a0 + [a1α + ... + αλ-1αλ-1])p ≡ (a0)p + (a1α + [... + αλ-1αλ-1])p (mod p).
(4) We could keep breaking out each element until we get:
(a0 + [a1α + ... + αλ-1αλ-1])p ≡ (a0)p + (a1α)p + ... + (aλ-1αλ-1)p (mod p)
(5) Now for each coefficient ai, using Lemma 2 above, we have:
aip ≡ ai (mod p)
So this gives us:
(a0)p + (a1α)p + ... + (aλ-1αλ-1)p ≡ a0 + a1αp + ... + aλ-1(αλ-1)p (mod p)
(6) And we are done since this shows that:
g(α)p ≡ g(αp) (mod p)
QED
Cyclotomic Integers: Periods
In today's blog, I will review the concept of periods for cyclotomic integers from Harold Edward's Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory. I am continuing down the same chapter that I started in an earlier blog. If you would like to start at the beginning of cyclotomic integer properties, start here.
I will continue to use Edward's σg(α) notation that I reviewed in a previous blog.
Lemma 1:
Let e be a factor of λ - 1 where λ is an odd prime and α is a primitive root of unity where αλ = 1.
Then, for a given cyclotomic integer g(α) there exists a cyclotomic integer G(α) such that:
Ng(α) = G(α)*σG(α)*...*σe-1G(α)
Proof:
(1) Let G(α) = g(α)*σeg(α)*σ2eg(α)*...*σ-eg(α) where σ-e denotes σλ-1-e
(2) With this definition we can see that:
G(α) = g(α)*g(αγe)*g(αγ2e)*...*g(αγ(λ-1-e))
σG(α) = g(αγ)*g(αγ(e+1))*g(αγ2e+1)*...*g(αγλ-e)
...
σe-1G(α) = g(αγ(e-1))*g(αγ(2e-1))*...*g(αγ(λ-2))
(3) Putting this all together, we see that:
Ng(α) = g(α)*g(αγ)*g(αγ*γ)*...*g(αγ(λ-2))
(4) Since γ is a primitive root mod λ, we know that (3) is the same as:
Ng(α) = g(α)*g(α2)*g(α3)*..*g(αλ-1)
QED
Example 1: λ = 13, γ = 2, and e = 4
In this case, Ng(α) = G(α)G(α)G(α4)G(α8)
Each term G(α) = g(α)*g(α24)*g(α22*4) = g(α)*g(α3)*g(α9)
Since:
2 ≡ 2 (mod 13)
22 ≡ 4 (mod 13)
23 ≡ 8 (mod 13)
24 ≡ 16 ≡ 3 (mod 13)
25 ≡ 32 ≡ 6 (mod 13)
26 ≡ 64 ≡ 12 (mod 13)
27 ≡ 128 ≡ 11 (mod 13)
28 ≡ 256 ≡ 9 (mod 13)
29 ≡ 512 ≡ 5 (mod 13)
210 ≡ 1024 ≡ 10 (mod 13)
211 ≡ 2048 ≡ 7 (mod 13)
212 ≡ 4096 ≡ 1 (mod 13)
Corollary 1.1: σeG(α) = G(α)
Proof:
(1) G(α) = g(α)*g(αγe)*g(αγ2e)*...*g(αγ(λ-1-e))
(2) And we find that:
σeG(α) = g(αγe)*g(αγ2e)*g(αγ3e)*...*g(αγλ-1)
(3) And since γλ-1 ≡ 1 (mod λ) (By Fermat's Little Theorem), we see that the result in step #2 is the same as the result in step #1.
QED
Corollary 1.2: σeG(α) = G(α) implies that there exists a set of e cyclotomic integers: η0, η1, ... ηe-1 such that:
(a) η0 = α + σeα + σ2eα + ... + σλ-1-eα
(b) ηi+1 = σηi
(c) G(α) = a0 + a1η0 + a2η1 + ... + aeηe-1 where ai are integers.
Proof:
(1) σeG(α) = G(α)
(2) Since G(α) is a cyclotomic integer, we know that (see Lemma 1 here):
G(α) = a0 + a1α + ... + aλ-1αλ-1
(3) Now, (#1) implies that the coefficient for any αj, αj = σeαj
(4) In order for #3 to be true, then G(α) must have the following form:
G(α) = a0 + a1(α + σeα + σ2eα + ... + σλ-1-e) + a2(σα + σσeα + ...) + ... + ae(σe-1α + σe-1σeα + ...)
The reason being that each time all the values G(α) shifts by e, the new value must also have had the same coefficient and further, all new resulting values must be the same as values that existed before the shift. For each coefficient, the set of possible αj values must be closed.
(5) Now, we can define η0 in the following way:
η0 = α + σeα + σ2eα + ... + σλ-1-e
(6) We can likewise define ηi+1 as:
ηi+1 = σηi
(7) Putting (5) and (6) into the equation in step #4 gives us:
G(α) = a0 + a1η0 + ... + aeηe-1
QED
Definition 1: Cyclotomic Period
Let λ be a prime integer. Let α be a primitive root of unity such that αλ=1. Let γ be a primitive root modulo λ. Let e be a factor of λ - 1.
Let G(α) = g(α)*g(αγe)*g(αγ2e)*...*g(αγ(λ-1-e))
Then there exists a set of e cyclotomic integers: η0, η1, ... ηe-1 such that:
(a) η0 = α + σeα + σ2eα + ... + σλ-1-eα
(b) ηi+1 = σηi
(c) G(α) = a0 + a1η0 + a2η1 + ... + aeηe-1 where ai are integers.
The cyclotomic integers η0, η1, ... ηe-1 that meet conditions (a), (b), and (c) are called cyclotomic periods.
Note:
As a convention, ηe = η0 and η-1 = ηe-1. So one can think of ηi as an ever repeating pattern of e values such that ηi+1 = σηi
In this way, ηi is defined for all integers i.
Example 1: period for λ = 13, μ = 2, γ = 4
In this case, the cyclotomic periods are:
η0 = α + σ4α + σ8α = α + α3 + α9
η1 = σα + σα3 + σα9 = α2 + α6 + α5
η2 = σ2α + σ2α3 + σ2α9 = α4 + α12 + α10
η3 = σ3α + σ3α3 + σ3α9 = α8 + α11 + α7
Lemma 2: σeηi = ηi
Proof:
(1) For Case 0, this is given by the note in definition 1 above.
σeη0 = ηe = η0
(2) Let's assume that this is true up to i so that:
σeηi = ηi where 0 ≤ i.
(3) Then, this is also true for ηi+1 since:
σe(ηi+1) = σe(σηi) [From Definition 1 above]
Now σeσ = σe+1 = σσe
So that we get:
σeηi+1 = σ(σeηi)
By assumption at step #2, σeηi = ηi
So that we end up with:
σeηi+1 = σηi = ηi+1
(4) So, by the principle of induction, we are done.
QED
Lemma 3: Each period η consists of (λ-1)/e terms.
Proof:
(1) Let f = (λ - 1)/e.
(2) σefα = σλ-1α = α
(3) σ(λ - 1 - e)α = σe(f-1)α = (σe)f-1α
(4) So we can see that each term in α + σeα + σ2eα + ... + σλ-1-eα is σiα where i is 0*e, 1*e, 2*e, ... , (f-1)*e.
QED
Definition 2: Made up of periods of length f
A cyclotomic integer is made up of periods of length f if it can be put in the form:
a0 + a1η1 + a2η2 + ... + aeηe
where ai are integers and ηi are periods of length f.
Lemma 4: A cyclotomic integer g(α) is made up of periods of length if and only if σeg(α) = g(α)
Proof:
(1) Assume that g(α) is a cyclotomic integer made up of periods of length f.
(2) Then, there exists ai and ηi such that:
g(α) = a0 + a1η0 + a2η1 + ... + aeηe-1
(3) Applying σe to g(α) gives us:
σeg(α) = a0 + a1σeη0 + ... + aeσeηe-1
(4) Applying Lemma 2 above gives us:
σeg(α) = a0 + a1η0 + ... + aeηe-1
(5) Assume that σeg(α) = g(α)
(6) Then by Corollary 1.2 above, g(α) consists of e periods.
(7) And by Lemma 3, each period will be of length f.
QED
Corollary 4.1: The product of two cyclotomic integers made up of periods of length f is itself made up of periods of length f.
Proof:
(1) Let f(α), g(α) be cyclotomic integers made up of periods of length f so that:
σef(α) = f(α)
σeg(α) = g(α)
(2) But then:
σe[f(α)g(α)] = [σef(α)][σeg(α)] = f(α)g(α)
(3) So that by Lemma 4 above, we have proved that f(α)g(α) must itself be made up of periods of length f.
QED
Example: λ = 13, f = 3, e = 4
We note that:
(η0)2 = η1 + 2η2
η0η1 = η0 + η1 + η3
η0η2 = 3 + η1 + η3
Likewise, applying σ to these equations gives us:
(η1)2 = η2 + 2η0
η1η2 = η1 + η2 + η0
And so forth.
I will continue to use Edward's σg(α) notation that I reviewed in a previous blog.
Lemma 1:
Let e be a factor of λ - 1 where λ is an odd prime and α is a primitive root of unity where αλ = 1.
Then, for a given cyclotomic integer g(α) there exists a cyclotomic integer G(α) such that:
Ng(α) = G(α)*σG(α)*...*σe-1G(α)
Proof:
(1) Let G(α) = g(α)*σeg(α)*σ2eg(α)*...*σ-eg(α) where σ-e denotes σλ-1-e
(2) With this definition we can see that:
G(α) = g(α)*g(αγe)*g(αγ2e)*...*g(αγ(λ-1-e))
σG(α) = g(αγ)*g(αγ(e+1))*g(αγ2e+1)*...*g(αγλ-e)
...
σe-1G(α) = g(αγ(e-1))*g(αγ(2e-1))*...*g(αγ(λ-2))
(3) Putting this all together, we see that:
Ng(α) = g(α)*g(αγ)*g(αγ*γ)*...*g(αγ(λ-2))
(4) Since γ is a primitive root mod λ, we know that (3) is the same as:
Ng(α) = g(α)*g(α2)*g(α3)*..*g(αλ-1)
QED
Example 1: λ = 13, γ = 2, and e = 4
In this case, Ng(α) = G(α)G(α)G(α4)G(α8)
Each term G(α) = g(α)*g(α24)*g(α22*4) = g(α)*g(α3)*g(α9)
Since:
2 ≡ 2 (mod 13)
22 ≡ 4 (mod 13)
23 ≡ 8 (mod 13)
24 ≡ 16 ≡ 3 (mod 13)
25 ≡ 32 ≡ 6 (mod 13)
26 ≡ 64 ≡ 12 (mod 13)
27 ≡ 128 ≡ 11 (mod 13)
28 ≡ 256 ≡ 9 (mod 13)
29 ≡ 512 ≡ 5 (mod 13)
210 ≡ 1024 ≡ 10 (mod 13)
211 ≡ 2048 ≡ 7 (mod 13)
212 ≡ 4096 ≡ 1 (mod 13)
Corollary 1.1: σeG(α) = G(α)
Proof:
(1) G(α) = g(α)*g(αγe)*g(αγ2e)*...*g(αγ(λ-1-e))
(2) And we find that:
σeG(α) = g(αγe)*g(αγ2e)*g(αγ3e)*...*g(αγλ-1)
(3) And since γλ-1 ≡ 1 (mod λ) (By Fermat's Little Theorem), we see that the result in step #2 is the same as the result in step #1.
QED
Corollary 1.2: σeG(α) = G(α) implies that there exists a set of e cyclotomic integers: η0, η1, ... ηe-1 such that:
(a) η0 = α + σeα + σ2eα + ... + σλ-1-eα
(b) ηi+1 = σηi
(c) G(α) = a0 + a1η0 + a2η1 + ... + aeηe-1 where ai are integers.
Proof:
(1) σeG(α) = G(α)
(2) Since G(α) is a cyclotomic integer, we know that (see Lemma 1 here):
G(α) = a0 + a1α + ... + aλ-1αλ-1
(3) Now, (#1) implies that the coefficient for any αj, αj = σeαj
(4) In order for #3 to be true, then G(α) must have the following form:
G(α) = a0 + a1(α + σeα + σ2eα + ... + σλ-1-e) + a2(σα + σσeα + ...) + ... + ae(σe-1α + σe-1σeα + ...)
The reason being that each time all the values G(α) shifts by e, the new value must also have had the same coefficient and further, all new resulting values must be the same as values that existed before the shift. For each coefficient, the set of possible αj values must be closed.
(5) Now, we can define η0 in the following way:
η0 = α + σeα + σ2eα + ... + σλ-1-e
(6) We can likewise define ηi+1 as:
ηi+1 = σηi
(7) Putting (5) and (6) into the equation in step #4 gives us:
G(α) = a0 + a1η0 + ... + aeηe-1
QED
Definition 1: Cyclotomic Period
Let λ be a prime integer. Let α be a primitive root of unity such that αλ=1. Let γ be a primitive root modulo λ. Let e be a factor of λ - 1.
Let G(α) = g(α)*g(αγe)*g(αγ2e)*...*g(αγ(λ-1-e))
Then there exists a set of e cyclotomic integers: η0, η1, ... ηe-1 such that:
(a) η0 = α + σeα + σ2eα + ... + σλ-1-eα
(b) ηi+1 = σηi
(c) G(α) = a0 + a1η0 + a2η1 + ... + aeηe-1 where ai are integers.
The cyclotomic integers η0, η1, ... ηe-1 that meet conditions (a), (b), and (c) are called cyclotomic periods.
Note:
As a convention, ηe = η0 and η-1 = ηe-1. So one can think of ηi as an ever repeating pattern of e values such that ηi+1 = σηi
In this way, ηi is defined for all integers i.
Example 1: period for λ = 13, μ = 2, γ = 4
In this case, the cyclotomic periods are:
η0 = α + σ4α + σ8α = α + α3 + α9
η1 = σα + σα3 + σα9 = α2 + α6 + α5
η2 = σ2α + σ2α3 + σ2α9 = α4 + α12 + α10
η3 = σ3α + σ3α3 + σ3α9 = α8 + α11 + α7
Lemma 2: σeηi = ηi
Proof:
(1) For Case 0, this is given by the note in definition 1 above.
σeη0 = ηe = η0
(2) Let's assume that this is true up to i so that:
σeηi = ηi where 0 ≤ i.
(3) Then, this is also true for ηi+1 since:
σe(ηi+1) = σe(σηi) [From Definition 1 above]
Now σeσ = σe+1 = σσe
So that we get:
σeηi+1 = σ(σeηi)
By assumption at step #2, σeηi = ηi
So that we end up with:
σeηi+1 = σηi = ηi+1
(4) So, by the principle of induction, we are done.
QED
Lemma 3: Each period η consists of (λ-1)/e terms.
Proof:
(1) Let f = (λ - 1)/e.
(2) σefα = σλ-1α = α
(3) σ(λ - 1 - e)α = σe(f-1)α = (σe)f-1α
(4) So we can see that each term in α + σeα + σ2eα + ... + σλ-1-eα is σiα where i is 0*e, 1*e, 2*e, ... , (f-1)*e.
QED
Definition 2: Made up of periods of length f
A cyclotomic integer is made up of periods of length f if it can be put in the form:
a0 + a1η1 + a2η2 + ... + aeηe
where ai are integers and ηi are periods of length f.
Lemma 4: A cyclotomic integer g(α) is made up of periods of length if and only if σeg(α) = g(α)
Proof:
(1) Assume that g(α) is a cyclotomic integer made up of periods of length f.
(2) Then, there exists ai and ηi such that:
g(α) = a0 + a1η0 + a2η1 + ... + aeηe-1
(3) Applying σe to g(α) gives us:
σeg(α) = a0 + a1σeη0 + ... + aeσeηe-1
(4) Applying Lemma 2 above gives us:
σeg(α) = a0 + a1η0 + ... + aeηe-1
(5) Assume that σeg(α) = g(α)
(6) Then by Corollary 1.2 above, g(α) consists of e periods.
(7) And by Lemma 3, each period will be of length f.
QED
Corollary 4.1: The product of two cyclotomic integers made up of periods of length f is itself made up of periods of length f.
Proof:
(1) Let f(α), g(α) be cyclotomic integers made up of periods of length f so that:
σef(α) = f(α)
σeg(α) = g(α)
(2) But then:
σe[f(α)g(α)] = [σef(α)][σeg(α)] = f(α)g(α)
(3) So that by Lemma 4 above, we have proved that f(α)g(α) must itself be made up of periods of length f.
QED
Example: λ = 13, f = 3, e = 4
We note that:
(η0)2 = η1 + 2η2
η0η1 = η0 + η1 + η3
η0η2 = 3 + η1 + η3
Likewise, applying σ to these equations gives us:
(η1)2 = η2 + 2η0
η1η2 = η1 + η2 + η0
And so forth.
Cyclotomic Integers: σg(α) notation
In today's blog, I will review the σg(α) notation from Harold Edward's Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory. I am continuing down the same chapter that I started in an earlier blog. If you would like to start at the beginning of cyclotomic integer properties, start here.
I will use this notation later on when I go over Kummer's proof of Fermat's Last Theorem for regular primes.
Edwards offers the following notation in Section 4.5:
Definition: σg(α)
Let σ signify the conjugate αγ for a given cyclotomic integer where γ is a primitive root mod λ and λ is a prime integer and α is a primitive root of unity where αλ = 1.
Example 1: σg(α), σ2g(α)
For a given cyclotomic integer g(α), σg(α) = g(αγ) and σ2g(α) = g(αγγ)
Example 2: Ng(α) in terms of σg(α) [See here for more information on Ng(α) notation]
Using this new notation, since γ is a primitive root mod λ, we see that:
Ng(α) = g(α)*σg(α)*σ2g(α)*...*σλ-2g(α)
Example 3: σλ-1g(α)
Since σ is defined as α → αγ, and since the order of a primitive root is λ - 1 (see Theorem 1 here), we see that:
σλ-1 = g(α(λ-1)*(γ)) = g(α1) = g(α)
Note:
The advantage of this notation is that it avoids many of the subscripts that we have been using previously.
Based on the properties of primitive roots (see here), we can see that σg(α), σ2g(α), ..., σλ-1g(α) are all distinct.
I will use this notation later on when I go over Kummer's proof of Fermat's Last Theorem for regular primes.
Edwards offers the following notation in Section 4.5:
Definition: σg(α)
Let σ signify the conjugate αγ for a given cyclotomic integer where γ is a primitive root mod λ and λ is a prime integer and α is a primitive root of unity where αλ = 1.
Example 1: σg(α), σ2g(α)
For a given cyclotomic integer g(α), σg(α) = g(αγ) and σ2g(α) = g(αγγ)
Example 2: Ng(α) in terms of σg(α) [See here for more information on Ng(α) notation]
Using this new notation, since γ is a primitive root mod λ, we see that:
Ng(α) = g(α)*σg(α)*σ2g(α)*...*σλ-2g(α)
Example 3: σλ-1g(α)
Since σ is defined as α → αγ, and since the order of a primitive root is λ - 1 (see Theorem 1 here), we see that:
σλ-1 = g(α(λ-1)*(γ)) = g(α1) = g(α)
Note:
The advantage of this notation is that it avoids many of the subscripts that we have been using previously.
Based on the properties of primitive roots (see here), we can see that σg(α), σ2g(α), ..., σλ-1g(α) are all distinct.
Tuesday, May 23, 2006
Cyclotomic Integers: More x + αiy
In today's blog, I continue going through lemmas from Harold Edward's Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory. I am continuing down the same section that I started in my previous blog. If you would like to start at the beginning of cyclotomic integer properties, start here.
I will use many of these properties later when I go over Kummer's proof of Fermat's Last Theorem for regular primes.
Lemma 1:
if f(α) ≡ g(α) (mod h(α)) → f(k) ≡ g(k) (mod p) with αλ = 1 and λ is a prime.
then kλ ≡ 1 (mod p)
Proof:
(1) Let f(α) = αλ-1 + αλ-2 + ... + α + 1.
(2) We know that f(α) = 0 [See Lemma 2 here for proof if needed]
(3) So we have f(α) ≡ 0 (mod h(α)) [See here if you need a review of modular arithmetic]
(4) But from assumption f(α) ≡ g(α) (mod h(α) → f(k) ≡ g(k) (mod p) so:
f(k) ≡ 0 (mod p)
(5) So kλ-1 + kλ-2 + ... + k + 1 ≡ 0 (mod p)
(6) Now, if we multiply (k-1) to this result:
(k-1)(kλ-1 + kλ-2 + ... + k + 1) =
= kλ + kλ-1 + ... + k2 + k - kλ-1 - kλ-2 - ... - k - 1 =
= kλ - 1
(7) Now combining step #5 and step #6 gives us:
kλ - 1 ≡ 0 (mod p)
Which is the same as:
kλ ≡ 1 (mod p)
QED
Lemma 2:
If k is an integer and p is a prime such that kj ≡ 1 (mod p)
Then, there exists a smallest nonzero integer d such that kj ≡ 1 (mod p) if and only if d divides j.
Proof:
(1) By the Well-Ordering Principle, we know that there must be a smallest nonzero integer where kd ≡ 1 (mod p)
(2) Let us assume that kj ≡ 1 (mod p) but d doesn't divide j.
(3) Using the Division Algorithm, we know that there exists q,r such that:
j = dq + r and 1 ≤ r ≤ d-1
(4) Then kj ≡ 1 (mod p) implies that:
kdq+r ≡ 1 (mod p)
and further, we note that:
kdq + r ≡ (kdq)*(kr) ≡ [(kd)q]*(kr) ≡ (1)(kr) ≡ kr ≡ 1 (mod p)
(5) But this is impossible since d is the lowest nonzero value such that kd ≡ 1 (mod p) so we reject our assumption in #2.
(6) Now, let's assume that d divides j.
(7) So, then there exists a value q such that:
kj ≡ kdq ≡ (kd)q ≡ (1)q ≡ 1 (mod p).
QED
Lemma 3:
If h(α) is a prime cyclotomic integer which divides a binomial x + αjy (where x,y are relatively prime integers and αj ≠ 1) and αλ = 1 where λ is a prime.
Then there exists a prime p such that h(α) divides p and either p = λ or p ≡ 1 (mod λ)
Proof:
(1) Let h(α) be a prime cyclotomic integer which divides a binomial x + αjy
(2) We know that there exists a prime p such that h(α) divides p. [See Lemma 1 here for proof]
(3) We know from Lemma 1 above that there exists an integer k such that:
kλ ≡ 1 (mod p)
(4) We also know from Lemma 2 above that there exists a minimum element d such that αd ≡ 1 (mod p) and since αλ ≡ 1 (mod p), we know that d = 1 or d = λ
(5) Assume d = 1.
We will show that this implies that λ = p
(6) Then k1 ≡ 1 (mod p)
(7) From Lemma 1 above, we know that:
kλ-1 + kλ-2 + ... + k + 1 ≡ 0 (mod p)
So applying step #6 gives us:
(1)λ-1 + (1)λ-2 + ... + (1)1 + 1 ≡ λ ≡ 0 (mod p)
(8) This implies that p divides λ but since both p, λ are primes, this is only possible if λ = p.
(9) Assume d= λ.
We will show that this implies that p ≡ 1 (mod λ)
(10) Using Fermat's Little Theorem, we know that:
kp-1 ≡ 1 (mod p)
(11) From Lemma 2 above, this tells us that λ must divide p-1.
(12) So that we conclude that p ≡ 1 (mod λ)
QED
Lemma 4: if n is an odd prime, then
(x - α)(x - α2)*...*(x - αn-1) = xn-1 + xn-2 + ... + 1
Proof:
(1) From a previous result, we have:
xn - 1 = (x - 1)(x - α)(x - α2)*...*(x - αn-1)
(2) Now xn - 1 divided by x-1 = xn-1 + xn-2 + ... + x + 1 since:
(x-1)(xn-1 + xn-2 + ... + x + 1) =
= xn + xn-1 + xn-2 + .... + x2 + x -xn-1 - xn-2 - .... - x2 - x - 1 =
= xn - 1
(3) Putting #2 and #1 together gives us:
xn-1 + xn-2 + ... + x + 1 = (x - α)(x - α2) * ... * (x - αn-1)
QED
Lemma 5:
if h(αj) divides h(αi) where i is not congruent to j modulo λ then
Nh(α) divides N(αj-i-1)
Proof:
(1) Let k be an integer such that k ≡ α (mod hα) [For proof that this value exists, see Lemma 3 here]
(2) Since conjugates preserve relations (see Lemma 2.5 here), we also know that:
αj ≡ k (mod h(αj))
αi ≡ k (mod h(αi))
(3) Since h(αj) divides h(αi), we also have:
αi ≡ k (mod h(αj))
(4) Combining #2 and #3 gives us:
αj ≡ k ≡ αi (mod h(αj))
(5) So h(αj) divides αj - αi
(6) So Nh(αj) divides N(αj - αi) [See Lemma 6 here]
(7) But since Nh(α) = Nh(αj) (see Lemma 3 here), this gives us that:
Nh(α) divides N(αj - αi)
(8) Now, since αj - αi = αi(αj-i - 1), it follows that (see Lemma 6 here):
N(αj - αi) = N(αi)*N(αj-i-1)
(9) Finally, N(αi) = 1 since:
(a) N(αi) = N(α) = α*α2*...*αλ-1 = α1+2+3+...+λ-1
(b) 1 + 2 + 3 + ... + λ - 1 = (1/2)(λ - 1)λ since:
(1 + λ - 1) + (2 + λ - 2) + ... + (λ - 1 + 1) = 2 * (1 + 2 + 3 + ... + λ - 1)
Further, this result is = to (1 + λ -1) = λ so that we have (λ - 1)*(λ) = 2*(1 + 2 + 3 + ... + λ -1)
So dividing both sides by 2 gives us:
(1/2)(λ - 1)*(λ) = 1 + 2 + 3 +... + λ - 1)
(c) Since λ is odd, we know that λ - 1 is even so there exists a rational integer x such that x = (1/2)(λ - 1)
(d) So we get: 1 + 2 + 3 + ... + λ - 1 = x(λ)
(e) So putting it all together:
N(α) = α1 + 2 + 3 + ... + λ-1 = αx(λ)) = (αλ)x = 1.
(10) So, Nh(α) divides N(αj-i - 1)
QED
Lemma 6:
If h(α) is a prime cyclotomic integer which divides a binomial x + αjy (where x,y are relatively prime integers and αj ≠ 1),
then Nh(α) is a prime integer which is congruent to 0 or 1 modulo λ
Proof:
(1) Let h(α) be a prime cyclotomic integer that divides x + αjy.
(2) Then, there exists a prime integer p such that h(α) divides p. [See Lemma 1 here for proof]
(3) Using Lemma 3 above we know that p ≡ 0 (mod λ) or p ≡ 1 (mod λ).
(4) From a previous result (Lemma 3 here), we know that there exists an integer k such that:
k ≡ α (mod h(α))
(5) Assume p = λ (see Lemma 3 above since this is the case where p ≡ 0 (mod λ))
We will now show that N(h(α)) = p.
(6) There exists an integer d such that d is the minimum positive integer where kd ≡ 1 (mod p) [See Lemma 2 above]
(7) Then d = 1 since (from Lemma 3 above) if d ≠ 1, then d = λ which implies that p ≡ 1 (mod λ) which contradicts assumption in #4 so we conclude d=1.
(8) So k ≡ 1 (mod p) since kd ≡ 1 (mod p) [See Lemma 3 above for details if needed]
(9) So, combining step #8 with step #4 gives us:
α ≡ 1 (mod p)
and since h(α) divides p, this also gives us:
α ≡ 1 (mod h(α))
(10) This shows that h(α) divides α - 1.
(11) This also shows that Nh(α) divides N(α - 1) [See Lemma 6 here for details if needed]
(12) N(α - 1) = N(1 - α) since:
N(α - 1) = (α - 1)(α2 - 1)*...*(αn-1 - 1)
N(1 - α) = (-1)n-1[(α - 1)(α2 - 1)*..*(αn-1 - 1)
Since n is odd, n-1 is even and (-1)n-1 = 1
(13) N(1 - α) = (1 - α)(1 - α2)*...*(1 - αn-1) [See here for definition of norm for cyclotomic integers]
(14) From Lemma 4 above:
(x - α)(x - α2)*...*(x - αn-1) = xn-1 + xn-2 + ... + x + 1
(15) Setting x = 1 gives us:
(1 - α)(1 - α2)*...*(1 - αn-1) = 1n-1 + 1n-2 + ... + 1 + 1 = n
(16) Since in this case n= λ, this proves that N(α - 1) = λ
(17) Now h(α) divides (α - 1) (step #10), this also gives us that Nh(α) divides N(α - 1) which means that Nh(α) divides p.
(18) But p is a prime and since Nh(α) ≠ 1 (since h(α) is a cyclotomic prime, see here for more details), we are left with concluding that Nh(α) = p.
(19) Assume p ≡ 1 (mod λ).
We will now show that under this condition, Nh(α) = p
(20) Since k ≡ α (mod h(α)) [from step #4] we know that:
(a) h(α) divides k - α
(b) And therefore h(αj) divides k - αj since conjugates preserve relations (see Lemma 2.5 here)
(21) Now we know that no conjugate of h(αi) divides another conjugate of h(αj) where i is not congruent to j modulo λ since:
(a) Assume h(αj) divides h(αi) and i is not congruent to j (mod h(α))
(b) Then Nh(α) divides N(αj-i-1) [See Lemma 5 above]
(c) But since i is not congruent to j (mod h(α)), N(αj-i-1) = N(α - 1) [See Lemma 5 above]
(d) So that using the reasoning from #12 thru #16 gives us that:
N(αj-i-1) = λ
(e) But then h(α) divides λ which is impossible since p does not divide λ from step #19 so we have a contradiction and we reject our assumption in step #21a.
(22) Since h(α) divides p, there exists a cyclotomic integer q(α) such that:
p = h(α)*q(α)
(23) Now we know that each of the other conjugates of h(α) must also divide p since h(α) divides p implies Nh(α) divides N(p) so that h(α)*h(α2)*...h(αn-1) divides p*p*...*p.
(24) Since h(α2) divides p, it divides h(α)*q(α) but it cannot divide h(α) from step #21 so it divides q(α) [See here for reason that Euclid's Lemma applies to cyclotomic integers]
(25) We can therefore conclude that there exists q2(α) such that q(α) = h(α2)*q2(α)
(26) We can repeat step #24 and step #25 for each conjugate of h(α) until we get:
p = h(α)*h(α2)*...h(αn-1)*qn-1(α)
So that we get:
p = Nh(α)*qn-1(α)
(27) But since p is a prime integer and Nh(α) is a rational integer, qn-1(α) must also be a rational integer.
(28) But p is prime so the only values that can divide it are p and 1. Since we know that Nh(α) ≠ 1, this means that Nh(α) = p and qn-1(α) = 1.
QED
Corollary 6.1: If Nh(α) = λ, then h(α) and all of its conjugates are unit multiples of α - 1.
Proof:
(1) Let Nh(α) = λ
(2) From Lemma 6 above, we know that there exists an integer k such that k ≡ 1 (mod p)
(3) Since k ≡ α (mod p) (from Lemma 6 above), this also means that α ≡ 1 (mod p).
(4) This shows that p divides α - 1 which means likewise that h(α) divides α - 1 since h(α) divides p.
(5) Then, there exists a value q(α) such that α - 1 = h(α)q(α)
(6) Using Lemma 6 here, we get:
N(α - 1) = Nh(α)*Nq(α)
(7) From step #16 in Lemma 6 above, we know that N(α - 1) = λ
(8) But we also know from Lemma 6 above that Nh(α) = p = λ
(9) So we see that Nq(α) = 1 which means that q(α) is a cyclotomic unit (see here for definition of a cyclotomic unit)
(10) Since all the conjugates of h(α) divide p (see Lemma 6 above for details), we can make the same argument for each of them.
QED
Lemma 7:
If h(α) is any cyclotomic integer whose norm is a prime integer, then h(α) is prime and it divides a binomial x + αjy (x,y relatively prime, αj ≠ 1)
Proof:
(1) Let h(α) be a cyclotomic integer whose norm Nh(α) is a prime integer p
(2) Let k be an integer such that kλ ≡ 1 (mod p) where λ is an odd prime.
(3) Let γ be a primitive root mod p. (See here for details on primitive roots if needed)
(4) Then every nonzero integer mod p can be written in a form of γi where i = 1, 2, ..., p - 1). [See here for definition of primitive root]
(5) We also see that by Fermat's Little Theorem, (γi)λ ≡ 1 (mod p) if and only if p-1 divides iλ
(6) In Lemma 6 above, this theorem has been proven for the case p = λ so we can assume that p ≡ 1 (mod λ)
(7) Based on this assumption, there exists a value μ such that p - 1 = λμ
(8) From step #5, we know that p-1 divides iλ if and only if μ divides i since:
(a) From step #7, μ = (p-1)/λ
(b) Assume p - 1 divides iλ
(c) p-1 = λ*μ
(d) So λ*μ divides i λ
(e) Since λ cancels out, this means that μ must divide i.
(f) Assume μ divides i
(g) Then λ*μ divides i*λ
(h) Which means that p-1 divides i*λ
(9) Let m = γμ
(10) If k = m, m2, m3, ..., then:
kλ ≡ 1 (mod p) [This follows from step #8, step #9]
(11) h(m)*h(m2)*...*h(mλ-1) ≡ 0 (mod p) since:
(a) Using the Division Algorithm for polynomials (see here), we know that there exists q(x), r(x) such that:
h(x)*h(x2)*...*h(xλ-1) = q(x)(xλ-1 + xλ-2 + ... + 1) + r(x)
where the degree of r(x) is a polynomial of degree less than λ - 1.
(b) Since Nh(α) = p and since αλ-1 + αλ - 2 + ... + 1 = 0 (see Lemma 2 here), we get:
p = q(α)(0) + r(α)
so that r(x) = p
(c) Using step #11b, we get:
h(m)*h(m2)*...*h(mλ-1) = q(m)(mλ-1 + mλ - 2 + ... + 1) + p.
(d) Now, from an earlier result (see step #6 in Lemma 1 above), we know that:
(mλ - 1)/(m - 1) = mλ-1 + mλ - 2 + ... + 1
(e) We also know that m is not congruent 1 (mod p) since:
μ divides p-1 from step #7 above
So μ is less than p-1.
The order of γ is p-1 [See here for definition of order of a primitive root]
So therefore m = γμ cannot be congruent to 1 (mod p)
(f) Since mλ ≡ 1 (mod p) from step #10 and since m is not congruent 1 (mod p) , we get:
(mλ - 1)/(m - 1) ≡ (1 - 1)/(m - 1) ≡ 0 (mod p)
(12) From this, we know that at least one of the values h(mj) ≡ 0 (mod p)
(13) Using the Division Algorithm for Polynomials with h(x), we have:
h(x) = q(x)(x - mj) + r where 1 ≤ j ≤ λ -1.
We see that r is an integer.
(13)Using h(mj) = q(mj)(mj - mj) + r shows that r = h(mj) and from step #12, we can assume that r ≡ 0 (mod p)
(14) So h(αi) ≡ q(αi)(αi - mj) (mod p) for i = 1, 2, ..., λ - 1.
(15) Now, from step #14, we get:
(α - mj)*h(α2)*h(α3)*...*h(αλ-1) ≡
≡ (α - mj)q(α2)(α2 - mj)q(α3)*(α3 - mj)* ... * q(αλ-1)(αλ-1 - mj) ≡
≡ N(α - mj)q(α2)q(α3)*...*q(αλ-1) (mod p)
(16) Now, since (x - α)*...*(x - αλ-1) = (xλ - 1)/(x - 1) [See here], we know that:
N(α - k) = (kλ - 1)/(k - 1) ≡ (1 - 1)/(k - 1) ≡ 0 (mod p)
(17) And since k can equal mj (see step #10), we have shown that N(α - mj) ≡ 0 (mod p).
(18) This proves that h(α) divides α - mj since h(α) divides p.
(19) Now, we need only to prove that h(α) is prime to complete the proof.
(20) Assume that h(α) divides f(α)g(α)
(21) Then f(α)g(α) ≡ 0 (mod h(α))
(22) Since α ≡ k (mod h(α)), we also have:
f(k)g(k) ≡ 0 (mod h(α))
(23) We also have f(k)g(k) ≡ 0 (mod p) since:
(a) Assume f(k)g(k) ≡ w (mod p) and w is not congruent to 0.
(b) Then f(k)g(k) ≡ w (mod h(α)) since h(α) divides p.
(c) And then w ≡ 0 (mod h(α)) which is impossible so we reject our assumption at (#23a)
(24) Now p either divides f(k) or g(k) by Euclid's Lemma.
(25) So finally, h(α) must divide either f(k) or g(k).
(26) And since k ≡ α (mod h(α)), we also have:
h(α) must divide either f(α) or g(α).
QED
I will use many of these properties later when I go over Kummer's proof of Fermat's Last Theorem for regular primes.
Lemma 1:
if f(α) ≡ g(α) (mod h(α)) → f(k) ≡ g(k) (mod p) with αλ = 1 and λ is a prime.
then kλ ≡ 1 (mod p)
Proof:
(1) Let f(α) = αλ-1 + αλ-2 + ... + α + 1.
(2) We know that f(α) = 0 [See Lemma 2 here for proof if needed]
(3) So we have f(α) ≡ 0 (mod h(α)) [See here if you need a review of modular arithmetic]
(4) But from assumption f(α) ≡ g(α) (mod h(α) → f(k) ≡ g(k) (mod p) so:
f(k) ≡ 0 (mod p)
(5) So kλ-1 + kλ-2 + ... + k + 1 ≡ 0 (mod p)
(6) Now, if we multiply (k-1) to this result:
(k-1)(kλ-1 + kλ-2 + ... + k + 1) =
= kλ + kλ-1 + ... + k2 + k - kλ-1 - kλ-2 - ... - k - 1 =
= kλ - 1
(7) Now combining step #5 and step #6 gives us:
kλ - 1 ≡ 0 (mod p)
Which is the same as:
kλ ≡ 1 (mod p)
QED
Lemma 2:
If k is an integer and p is a prime such that kj ≡ 1 (mod p)
Then, there exists a smallest nonzero integer d such that kj ≡ 1 (mod p) if and only if d divides j.
Proof:
(1) By the Well-Ordering Principle, we know that there must be a smallest nonzero integer where kd ≡ 1 (mod p)
(2) Let us assume that kj ≡ 1 (mod p) but d doesn't divide j.
(3) Using the Division Algorithm, we know that there exists q,r such that:
j = dq + r and 1 ≤ r ≤ d-1
(4) Then kj ≡ 1 (mod p) implies that:
kdq+r ≡ 1 (mod p)
and further, we note that:
kdq + r ≡ (kdq)*(kr) ≡ [(kd)q]*(kr) ≡ (1)(kr) ≡ kr ≡ 1 (mod p)
(5) But this is impossible since d is the lowest nonzero value such that kd ≡ 1 (mod p) so we reject our assumption in #2.
(6) Now, let's assume that d divides j.
(7) So, then there exists a value q such that:
kj ≡ kdq ≡ (kd)q ≡ (1)q ≡ 1 (mod p).
QED
Lemma 3:
If h(α) is a prime cyclotomic integer which divides a binomial x + αjy (where x,y are relatively prime integers and αj ≠ 1) and αλ = 1 where λ is a prime.
Then there exists a prime p such that h(α) divides p and either p = λ or p ≡ 1 (mod λ)
Proof:
(1) Let h(α) be a prime cyclotomic integer which divides a binomial x + αjy
(2) We know that there exists a prime p such that h(α) divides p. [See Lemma 1 here for proof]
(3) We know from Lemma 1 above that there exists an integer k such that:
kλ ≡ 1 (mod p)
(4) We also know from Lemma 2 above that there exists a minimum element d such that αd ≡ 1 (mod p) and since αλ ≡ 1 (mod p), we know that d = 1 or d = λ
(5) Assume d = 1.
We will show that this implies that λ = p
(6) Then k1 ≡ 1 (mod p)
(7) From Lemma 1 above, we know that:
kλ-1 + kλ-2 + ... + k + 1 ≡ 0 (mod p)
So applying step #6 gives us:
(1)λ-1 + (1)λ-2 + ... + (1)1 + 1 ≡ λ ≡ 0 (mod p)
(8) This implies that p divides λ but since both p, λ are primes, this is only possible if λ = p.
(9) Assume d= λ.
We will show that this implies that p ≡ 1 (mod λ)
(10) Using Fermat's Little Theorem, we know that:
kp-1 ≡ 1 (mod p)
(11) From Lemma 2 above, this tells us that λ must divide p-1.
(12) So that we conclude that p ≡ 1 (mod λ)
QED
Lemma 4: if n is an odd prime, then
(x - α)(x - α2)*...*(x - αn-1) = xn-1 + xn-2 + ... + 1
Proof:
(1) From a previous result, we have:
xn - 1 = (x - 1)(x - α)(x - α2)*...*(x - αn-1)
(2) Now xn - 1 divided by x-1 = xn-1 + xn-2 + ... + x + 1 since:
(x-1)(xn-1 + xn-2 + ... + x + 1) =
= xn + xn-1 + xn-2 + .... + x2 + x -xn-1 - xn-2 - .... - x2 - x - 1 =
= xn - 1
(3) Putting #2 and #1 together gives us:
xn-1 + xn-2 + ... + x + 1 = (x - α)(x - α2) * ... * (x - αn-1)
QED
Lemma 5:
if h(αj) divides h(αi) where i is not congruent to j modulo λ then
Nh(α) divides N(αj-i-1)
Proof:
(1) Let k be an integer such that k ≡ α (mod hα) [For proof that this value exists, see Lemma 3 here]
(2) Since conjugates preserve relations (see Lemma 2.5 here), we also know that:
αj ≡ k (mod h(αj))
αi ≡ k (mod h(αi))
(3) Since h(αj) divides h(αi), we also have:
αi ≡ k (mod h(αj))
(4) Combining #2 and #3 gives us:
αj ≡ k ≡ αi (mod h(αj))
(5) So h(αj) divides αj - αi
(6) So Nh(αj) divides N(αj - αi) [See Lemma 6 here]
(7) But since Nh(α) = Nh(αj) (see Lemma 3 here), this gives us that:
Nh(α) divides N(αj - αi)
(8) Now, since αj - αi = αi(αj-i - 1), it follows that (see Lemma 6 here):
N(αj - αi) = N(αi)*N(αj-i-1)
(9) Finally, N(αi) = 1 since:
(a) N(αi) = N(α) = α*α2*...*αλ-1 = α1+2+3+...+λ-1
(b) 1 + 2 + 3 + ... + λ - 1 = (1/2)(λ - 1)λ since:
(1 + λ - 1) + (2 + λ - 2) + ... + (λ - 1 + 1) = 2 * (1 + 2 + 3 + ... + λ - 1)
Further, this result is = to (1 + λ -1) = λ so that we have (λ - 1)*(λ) = 2*(1 + 2 + 3 + ... + λ -1)
So dividing both sides by 2 gives us:
(1/2)(λ - 1)*(λ) = 1 + 2 + 3 +... + λ - 1)
(c) Since λ is odd, we know that λ - 1 is even so there exists a rational integer x such that x = (1/2)(λ - 1)
(d) So we get: 1 + 2 + 3 + ... + λ - 1 = x(λ)
(e) So putting it all together:
N(α) = α1 + 2 + 3 + ... + λ-1 = αx(λ)) = (αλ)x = 1.
(10) So, Nh(α) divides N(αj-i - 1)
QED
Lemma 6:
If h(α) is a prime cyclotomic integer which divides a binomial x + αjy (where x,y are relatively prime integers and αj ≠ 1),
then Nh(α) is a prime integer which is congruent to 0 or 1 modulo λ
Proof:
(1) Let h(α) be a prime cyclotomic integer that divides x + αjy.
(2) Then, there exists a prime integer p such that h(α) divides p. [See Lemma 1 here for proof]
(3) Using Lemma 3 above we know that p ≡ 0 (mod λ) or p ≡ 1 (mod λ).
(4) From a previous result (Lemma 3 here), we know that there exists an integer k such that:
k ≡ α (mod h(α))
(5) Assume p = λ (see Lemma 3 above since this is the case where p ≡ 0 (mod λ))
We will now show that N(h(α)) = p.
(6) There exists an integer d such that d is the minimum positive integer where kd ≡ 1 (mod p) [See Lemma 2 above]
(7) Then d = 1 since (from Lemma 3 above) if d ≠ 1, then d = λ which implies that p ≡ 1 (mod λ) which contradicts assumption in #4 so we conclude d=1.
(8) So k ≡ 1 (mod p) since kd ≡ 1 (mod p) [See Lemma 3 above for details if needed]
(9) So, combining step #8 with step #4 gives us:
α ≡ 1 (mod p)
and since h(α) divides p, this also gives us:
α ≡ 1 (mod h(α))
(10) This shows that h(α) divides α - 1.
(11) This also shows that Nh(α) divides N(α - 1) [See Lemma 6 here for details if needed]
(12) N(α - 1) = N(1 - α) since:
N(α - 1) = (α - 1)(α2 - 1)*...*(αn-1 - 1)
N(1 - α) = (-1)n-1[(α - 1)(α2 - 1)*..*(αn-1 - 1)
Since n is odd, n-1 is even and (-1)n-1 = 1
(13) N(1 - α) = (1 - α)(1 - α2)*...*(1 - αn-1) [See here for definition of norm for cyclotomic integers]
(14) From Lemma 4 above:
(x - α)(x - α2)*...*(x - αn-1) = xn-1 + xn-2 + ... + x + 1
(15) Setting x = 1 gives us:
(1 - α)(1 - α2)*...*(1 - αn-1) = 1n-1 + 1n-2 + ... + 1 + 1 = n
(16) Since in this case n= λ, this proves that N(α - 1) = λ
(17) Now h(α) divides (α - 1) (step #10), this also gives us that Nh(α) divides N(α - 1) which means that Nh(α) divides p.
(18) But p is a prime and since Nh(α) ≠ 1 (since h(α) is a cyclotomic prime, see here for more details), we are left with concluding that Nh(α) = p.
(19) Assume p ≡ 1 (mod λ).
We will now show that under this condition, Nh(α) = p
(20) Since k ≡ α (mod h(α)) [from step #4] we know that:
(a) h(α) divides k - α
(b) And therefore h(αj) divides k - αj since conjugates preserve relations (see Lemma 2.5 here)
(21) Now we know that no conjugate of h(αi) divides another conjugate of h(αj) where i is not congruent to j modulo λ since:
(a) Assume h(αj) divides h(αi) and i is not congruent to j (mod h(α))
(b) Then Nh(α) divides N(αj-i-1) [See Lemma 5 above]
(c) But since i is not congruent to j (mod h(α)), N(αj-i-1) = N(α - 1) [See Lemma 5 above]
(d) So that using the reasoning from #12 thru #16 gives us that:
N(αj-i-1) = λ
(e) But then h(α) divides λ which is impossible since p does not divide λ from step #19 so we have a contradiction and we reject our assumption in step #21a.
(22) Since h(α) divides p, there exists a cyclotomic integer q(α) such that:
p = h(α)*q(α)
(23) Now we know that each of the other conjugates of h(α) must also divide p since h(α) divides p implies Nh(α) divides N(p) so that h(α)*h(α2)*...h(αn-1) divides p*p*...*p.
(24) Since h(α2) divides p, it divides h(α)*q(α) but it cannot divide h(α) from step #21 so it divides q(α) [See here for reason that Euclid's Lemma applies to cyclotomic integers]
(25) We can therefore conclude that there exists q2(α) such that q(α) = h(α2)*q2(α)
(26) We can repeat step #24 and step #25 for each conjugate of h(α) until we get:
p = h(α)*h(α2)*...h(αn-1)*qn-1(α)
So that we get:
p = Nh(α)*qn-1(α)
(27) But since p is a prime integer and Nh(α) is a rational integer, qn-1(α) must also be a rational integer.
(28) But p is prime so the only values that can divide it are p and 1. Since we know that Nh(α) ≠ 1, this means that Nh(α) = p and qn-1(α) = 1.
QED
Corollary 6.1: If Nh(α) = λ, then h(α) and all of its conjugates are unit multiples of α - 1.
Proof:
(1) Let Nh(α) = λ
(2) From Lemma 6 above, we know that there exists an integer k such that k ≡ 1 (mod p)
(3) Since k ≡ α (mod p) (from Lemma 6 above), this also means that α ≡ 1 (mod p).
(4) This shows that p divides α - 1 which means likewise that h(α) divides α - 1 since h(α) divides p.
(5) Then, there exists a value q(α) such that α - 1 = h(α)q(α)
(6) Using Lemma 6 here, we get:
N(α - 1) = Nh(α)*Nq(α)
(7) From step #16 in Lemma 6 above, we know that N(α - 1) = λ
(8) But we also know from Lemma 6 above that Nh(α) = p = λ
(9) So we see that Nq(α) = 1 which means that q(α) is a cyclotomic unit (see here for definition of a cyclotomic unit)
(10) Since all the conjugates of h(α) divide p (see Lemma 6 above for details), we can make the same argument for each of them.
QED
Lemma 7:
If h(α) is any cyclotomic integer whose norm is a prime integer, then h(α) is prime and it divides a binomial x + αjy (x,y relatively prime, αj ≠ 1)
Proof:
(1) Let h(α) be a cyclotomic integer whose norm Nh(α) is a prime integer p
(2) Let k be an integer such that kλ ≡ 1 (mod p) where λ is an odd prime.
(3) Let γ be a primitive root mod p. (See here for details on primitive roots if needed)
(4) Then every nonzero integer mod p can be written in a form of γi where i = 1, 2, ..., p - 1). [See here for definition of primitive root]
(5) We also see that by Fermat's Little Theorem, (γi)λ ≡ 1 (mod p) if and only if p-1 divides iλ
(6) In Lemma 6 above, this theorem has been proven for the case p = λ so we can assume that p ≡ 1 (mod λ)
(7) Based on this assumption, there exists a value μ such that p - 1 = λμ
(8) From step #5, we know that p-1 divides iλ if and only if μ divides i since:
(a) From step #7, μ = (p-1)/λ
(b) Assume p - 1 divides iλ
(c) p-1 = λ*μ
(d) So λ*μ divides i λ
(e) Since λ cancels out, this means that μ must divide i.
(f) Assume μ divides i
(g) Then λ*μ divides i*λ
(h) Which means that p-1 divides i*λ
(9) Let m = γμ
(10) If k = m, m2, m3, ..., then:
kλ ≡ 1 (mod p) [This follows from step #8, step #9]
(11) h(m)*h(m2)*...*h(mλ-1) ≡ 0 (mod p) since:
(a) Using the Division Algorithm for polynomials (see here), we know that there exists q(x), r(x) such that:
h(x)*h(x2)*...*h(xλ-1) = q(x)(xλ-1 + xλ-2 + ... + 1) + r(x)
where the degree of r(x) is a polynomial of degree less than λ - 1.
(b) Since Nh(α) = p and since αλ-1 + αλ - 2 + ... + 1 = 0 (see Lemma 2 here), we get:
p = q(α)(0) + r(α)
so that r(x) = p
(c) Using step #11b, we get:
h(m)*h(m2)*...*h(mλ-1) = q(m)(mλ-1 + mλ - 2 + ... + 1) + p.
(d) Now, from an earlier result (see step #6 in Lemma 1 above), we know that:
(mλ - 1)/(m - 1) = mλ-1 + mλ - 2 + ... + 1
(e) We also know that m is not congruent 1 (mod p) since:
μ divides p-1 from step #7 above
So μ is less than p-1.
The order of γ is p-1 [See here for definition of order of a primitive root]
So therefore m = γμ cannot be congruent to 1 (mod p)
(f) Since mλ ≡ 1 (mod p) from step #10 and since m is not congruent 1 (mod p) , we get:
(mλ - 1)/(m - 1) ≡ (1 - 1)/(m - 1) ≡ 0 (mod p)
(12) From this, we know that at least one of the values h(mj) ≡ 0 (mod p)
(13) Using the Division Algorithm for Polynomials with h(x), we have:
h(x) = q(x)(x - mj) + r where 1 ≤ j ≤ λ -1.
We see that r is an integer.
(13)Using h(mj) = q(mj)(mj - mj) + r shows that r = h(mj) and from step #12, we can assume that r ≡ 0 (mod p)
(14) So h(αi) ≡ q(αi)(αi - mj) (mod p) for i = 1, 2, ..., λ - 1.
(15) Now, from step #14, we get:
(α - mj)*h(α2)*h(α3)*...*h(αλ-1) ≡
≡ (α - mj)q(α2)(α2 - mj)q(α3)*(α3 - mj)* ... * q(αλ-1)(αλ-1 - mj) ≡
≡ N(α - mj)q(α2)q(α3)*...*q(αλ-1) (mod p)
(16) Now, since (x - α)*...*(x - αλ-1) = (xλ - 1)/(x - 1) [See here], we know that:
N(α - k) = (kλ - 1)/(k - 1) ≡ (1 - 1)/(k - 1) ≡ 0 (mod p)
(17) And since k can equal mj (see step #10), we have shown that N(α - mj) ≡ 0 (mod p).
(18) This proves that h(α) divides α - mj since h(α) divides p.
(19) Now, we need only to prove that h(α) is prime to complete the proof.
(20) Assume that h(α) divides f(α)g(α)
(21) Then f(α)g(α) ≡ 0 (mod h(α))
(22) Since α ≡ k (mod h(α)), we also have:
f(k)g(k) ≡ 0 (mod h(α))
(23) We also have f(k)g(k) ≡ 0 (mod p) since:
(a) Assume f(k)g(k) ≡ w (mod p) and w is not congruent to 0.
(b) Then f(k)g(k) ≡ w (mod h(α)) since h(α) divides p.
(c) And then w ≡ 0 (mod h(α)) which is impossible so we reject our assumption at (#23a)
(24) Now p either divides f(k) or g(k) by Euclid's Lemma.
(25) So finally, h(α) must divide either f(k) or g(k).
(26) And since k ≡ α (mod h(α)), we also have:
h(α) must divide either f(α) or g(α).
QED
Subscribe to:
Comments (Atom)
