Cyclotomic Integers: g(α)p ≡ g(αp) (mod p)

In today's blog, I continue to review results from Harold Edward's Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory. I am continuing down the same chapter that I started in an earlier blog. If you would like to start at the beginning of cyclotomic integer properties, start here.

Lemma 1: if p is a prime, then (x + y)^p ≡ x^p + y^p

Proof:

(1) Using the Binomial Theorem, we know that:




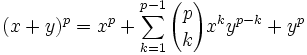
(2) Now, this means that each of the coefficients is equal to:



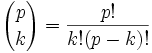
(3) But since p is a prime, p divides all coefficients.

For all values where k is between 1 and p-1, p, as a prime, will not be divisible by either k! or by (p-k)!.

(4) This means that p will divides (x + y)^p - x^p - y^p.

QED

Lemma 2: x^p ≡ x (mod p)

Proof:

(1) x^p - x = x(x^p-1 - 1)

(2) if gcd(x,p)=1, then by Fermat's Little Theorem, x^p-1 ≡ 1 (mod p) so p divides x^p-1-1.

(3) if p divides x, then of course p divides x(x^p-1-1)

QED

Lemma 3: g(α) ≡ g(α^p) mod p

Proof:

(1) Let g(α) = a₀ + a₁α + ... + α_λ-1α^λ-1.

(2) Then g(α)^p = (a₀ + [a₁α + ... + α_λ-1α^λ-1])^p

(3) Now using Lemma 1 above, we can break #2 out in the following ways:

(a₀ + [a₁α + ... + α_λ-1α^λ-1])^p ≡ (a₀)^p + (a₁α + [... + α_λ-1α^λ-1])^p (mod p).

(4) We could keep breaking out each element until we get:

(a₀ + [a₁α + ... + α_λ-1α^λ-1])^p ≡ (a₀)^p + (a₁α)^p + ... + (a_λ-1α^λ-1)^p (mod p)

(5) Now for each coefficient a_i, using Lemma 2 above, we have:

a_i^p ≡ a_i (mod p)

So this gives us:

(a₀)^p + (a₁α)^p + ... + (a_λ-1α^λ-1)^p ≡ a₀ + a₁α^p + ... + a_λ-1(α^λ-1)^p (mod p)

(6) And we are done since this shows that:

g(α)^p ≡ g(α^p) (mod p)

QED