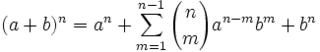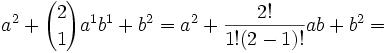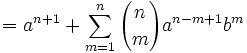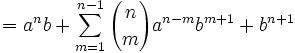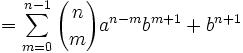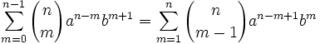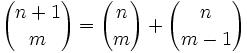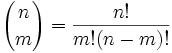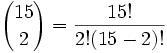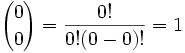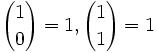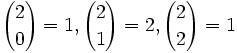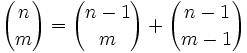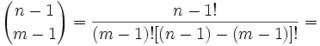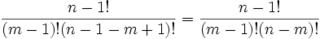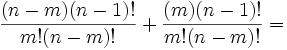Joseph-Louis Lagrange was born in Turin, Italy on January 25, 1736. His original name was Giuseppe Luigi Lagrangia. He would later change his name as he made Prussia and France his home.
Joseph-Louis Lagrange was born in Turin, Italy on January 25, 1736. His original name was Giuseppe Luigi Lagrangia. He would later change his name as he made Prussia and France his home.His father was a well-to-do mechant who worked for the King of Sardinia. Unfortunately, due to speculations, his father lost much of his wealth. Lagrange went to the college of Turin. He became interested in mathematics when he was 17 and he discovered a paper by Edmund Halley. Within one year, he had impressed the college with his skills in mathematics and became a lecturer at the artillery school.
When Lagrange was 19, he sent a letter to the famous mathematician Leonhard Euler describing a solution to the isoperimetrical problem. Euler was very impressed with Lagrange's method and conceded that it was superior to his own. Euler had been planning to publish his solution to the problem but after viewing Lagrange's solution, he withdrew his paper and let Lagrange publish the first solution to the problem. This paper helped to establish Lagrange as one of the top mathematicians of his time. The solution would serve as the foundation for what became known as the calculus of variations.
In 1758, Lagrange organized the Turin Academy which was a mathematical society that focused on mathematics. This group would go on to publish 5 volumes of mathematics. These volumes presented very high quality mathematics including topics such as a theory of the propagation of sound, a general differential equation for motion, a complete solution to an equation for a string vibrating traversely, recurring series, probabilities, more details on the calculus of variations, the principle of least action, integral calculus, number theory, and general differential equations for the motion of three bodies. By 1761, Lagrange had established himself as one of the greatest mathematician living. In 1764, he began his study of the libations of the moon and published his mathematical explanation for why the moon only displays the same face to the earth.
In 1766, Euler left Berlin. Frederick the Great invited Lagrange to come fill his post. Frederick wrote that the "greatest king in Europe" would like to have the "greatest mathematician of Europe" as resident in his royal court. Lagrange accepted his invitation and would stay in Prussia for the next 20 years.
While in Prussia, he wrote his famous Mecanique Analytique. His productivity at this point was amazing. He was producing a very high quality mathematical paper at the rate of one per month. He would spend his time thinking through each of his ideas and only when he had thought his ideas through did he write his papers. It is said that he was able to write out his papers complete without a single correction required. Topics included astronomical observations, pressure exerted by fluids in motion, integration by infinite series, a paper on the Jovian system, an essay on the problem of three bodies, secular equations of the moon, and cometary pertubations. In the course of these papers, he won many of the prizes (1772, 1774, and 1780) that were offered by the French Academy. Between 1772 and 1788, he worked to simplify Newton's equations. He reformulated Newtonian mechanics creating what is today known as Lagrangian mechanics.
In 1787, Frederick died and Lagrange accepted the offer of Louis XVI to move to Paris. He turned down invitations from Spain and Naples. He set up in residence in one of the special apartments of the Louvre. In 1792, he married for the second time.
The Reign of Terror began in 1793. In September 1793, an order was placed requiring all foreigners to leave France. He was able to get an exemption to this order based on the help of Antoine Lavoisier. Later, in 1798, his friend Lavoisier, after a trial that lasted only a day, was put to death by guillotine.
Lagrange wrote of his friend:
It took only a moment to cause this head to fall and a hundred years will not suffice to produce its like.In 1797, he became a professor of the Polytechnique Ecole in Paris. His lectures at the Polytechnique became very important and influential mathematical papers. It was here that he did his work on Continued Fractions and his mentorship of Sophie Germain.
Lagrange was still working on a revision of his Mecanique Analytique when he died in 1813. His achievements are astounding. He is one of the most prolific and important mathematicians of all time.
References
- Joseph-Louis Langrange, Wikipedia
- Biography of Lagrange, MacTutor