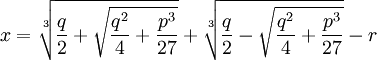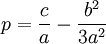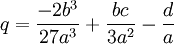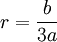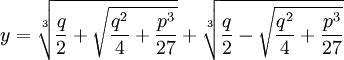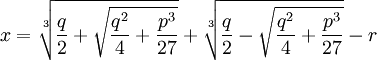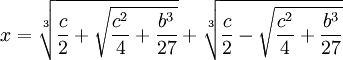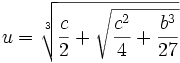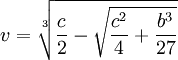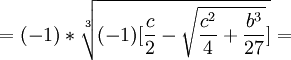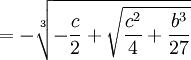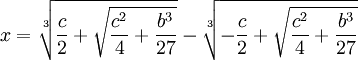Nicolo Fontana "Tartaglia" was born around 1500 in Venice. His father was a "mail rider", a person who would ride from town to town, to make deliveries. When Tartaglia was six years old, his father was murdered during one of these trips.
When Tartaglia was 12, the French took over his town of Brescia. There had been fierce fighting and in retaliation, there was a great slaughter of the Brescian townfolks. It is said that 46,000 inhabitants were killed in the fighting and the revenge killings. Tartaglia, his mother, and his sister hid away in a cathedral. In the course of the fighting, Tartaglia was attacked and left for dead.
Somehow, he survived but for the rest of his life, he bore terrible scars near his jaw and had difficulty speaking. It was in this way that he got his nickname "Tartaglia" which means "the stammerer". As an adult, he would always wear a beard in order to hide the scars.
Tartaglia took an interest in mathematics and demonstrated strong ability which earned him the patronage of Ludovico Balbisonio who paid for him to attend the University of Padua. By 1516, he had moved to Verona where he made his living by lecturing on mathematics.
In 1534, Tartaglia was working as a math teacher in Venice. While this was still a low paying position, he began to develop a reputation by participating in public mathematical challenges.
In 1535, there was a famous math contest between Tartaglia and Fior. Fior was a student of
Scipione del Ferro who had already solved the depressed cubic equation and had given the solution to Fior before he died. Tartaglia had by this time found a solution to one form of the cubic equation which was not directly solvable by the depressed cubic equation. Both Tartaglia and Fior submitted 30 problems that the other had to solve. Tartaglia could tell that Fior had a solution to the depressed cubic so he worked hard to find it. On February 13, 1535, Tartaglia solved the depressed cubic. Tartaglia easily solved all 30 of Fior's problems and won the contest.
Girolamo Cardano heard about Tartaglia's solution of the depressed cubic. Cardano, by this time, had a reputation as a brilliant and well-connected mathematician and physician. He approached Tartaglia with the hope of including Tartaglia's result in a book he was working on. Tartaglia declined.
Cardano promised to provide a letter of introduction to a very influential patron in Milan and invited Tartaglia to his home. Tartaglia, who still held his teacher's job, accepted Cardano's invitation to visit. While there, Cardano was able to convince Tartaglia to reveal his method for solving the depressed cubic. Cardano promised that he would not publish the solution without getting permission from Tartaglia.
Using Tartaglia's method, Cardano was able to solve the general cubic equation and his assistant
Lodovico Ferrari was able to solve the general quartic equation. Tartaglia refused to give Cardano permission to publish the method. It is probable that Tartaglia believed that he could use his method to continue to win math challenges.
When Cardano learned that Scipione del Ferro was the first to solve the depressed cubic, he decided to go ahead and publish his book
Ars Magna even without Tartaglia's permission. In the book, he gives Tartaglia and del Ferro credit for the solving the depressed cubic. He then shows how the general cubic equation can be reduced to a form of the depressed cubic.
This publishing of Cardano's book infuriated Tartaglia who proceeded to publish his own book called
New Problems and Inventions. In it, he attacked Cardano. Despite this, Cardano's book was a bestseller and established Cardano as the leading mathematician of his age.
Tartaglia challenged Cardano to a public math debate but Cardano refused. Cardano's assistant Ferrari offered to take up the challenge in Cardano's place. At this time, Ferrari was a relatively unknown mathematician and Tartaglia had little to gain from the challenge. On the other hand, if he had succeeded in challenging Cardano, because of Cardano's reputation, the debate could have helped his mathematical standing.
Tartaglia was offered a very lucrative post that he could get if he defeated Ferrari in the challenge. The math debate between Tartaglia and Ferrari occurred on August 10, 1548. Ferrari had clearly mastered the general cubic and quartic equations and it was very clear that Tartaglia would not be able to answer all of Ferrari's problems. Rather than admit this, Tartaglia left before the challenge completed.
Having lost the challenge, Tartaglia found that his existing position was threatened. In this way, Tartaglia saw his reputation collapse. It is said that for the rest of his life, he harbored resentment against Cardano. It is also said that he died in poverty. Tartaglia died on December 13, 1557.
References