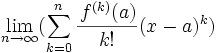In today's blog, I will go over
Taylor's Formula. This is a theorem that can be used to establish the
Taylor Series and the
MacLaurin Series which I use in my proof of
Euler's Identity.
If you are not familiar with continuous functions or closed intervals, start
here.
If you would like a review of derivatives, start
here.
Theorem: Taylor's FormulaLet
f(x) be a continuous function over the closed interval
[a,b] that has an
(n+1) derivative which is referenced by
f(n+1)(x) where
n is a positive integer.
Then:
f(b) = f(a) + f'(a)(b-a) + ... + [f(n)(a)/n!](b-a)n + [f(n+1)(z)/(n+1)!](b-a)n+1)for some number
z which lies between
a and
b.
Proof:
(1) Let
H = f(b) - f(a) - f'(a)(b-a) - [f''(a)/2!](b-a)2 - ... - [f(n)(a)/n!](b-a)n(2) Let
K = H/(b-a)n+1(3) Let
g(x) be a function such that:
g(x) = f(b) - f(x) - f'(x)(b-x) -[f''(x)/2!](b-x)2 - ... - [f(n)(x)/n!](b-x)n - K(b-x)n+1
(4) We can see that
g(x) is a continuous function since:
(a)
f(x) is continuous over
[a,b] by the given.
(b)
f(n) is a continuous function since by the given we know that
f(x) has an
(n+1) derivative and since
f(x) is differentiable at
x, then it is continuous at
x (see
here)
(c)
(b-x)n is continuous over
[a,b] since
f(x) is continuous since:
Let
h(x)=b-xh(x) is continuous since it is the addition of two continuous functions
i(x)=b and
j(x)=-x [See
here for proof of the Addition Law]
(b-x)n is continuous by the Multiplication Law [See
here for proof of the Multiplication Law]
(b-x)n = (b - x)*(b-x)*... since
n is a positive integer.
(d)
f(b) is continuous since it is a constant. (See
here)
(e) Each
f(n)(x)/n! is continuous since
(-1/n!) can be thought of as a constant function
h(x)=(-1/n!) and the multiplication of two continuous functions is itself continuous (see
here)
(f) Finally,
g(x) is continuous because the addition of a set of continuous functions is itself continuous (see
here)
(5) We can see that
g(a) = 0 since:
g(a) = H - H/(b-a)n+1*(b-a)n+1 = H - H = 0(6) We can also see that
g(b) = 0 since:
g(b) = f(b) - f(b) - f'(b)(b-b) - [f''(b)/2!](b-b)2 - ... - [f(n)(b)/n!](b-b)n - K(b-b)n+1(7) By Rolle's Theorem, since
g(x) is continuous on
[a,b], we know that there exists a value
z such that
z ∈ [a,b] and
g'(z) = 0. [See
here for Rolle's Theorem]
(8) If we differentiate on
g(x), we get:
g'(x) = -f'(x) + f'(x) -f(2)(x)(b-x) + f(2)(x)(b-x) - (1/2!)f(3)(x)(b-x)2 + (1/2!)f(3)(x)(b-x)2 - (1/3!)f(4)(x)(b-x)3 + ... + [1/(n-1)!]f(n)(x)(b-x)n-1 - (1/n!)f(n+1)(x)(b-x)n + (n+1)K(b-x)n since:
(a)
g(x) = f(b) - f(x) - f'(x)(b-x) -[f''(x)/2!](b-x)2 - ... - [f(n)(x)/n!](b-x)n - K(b-x)n+1(b) By Lemma 3
here, we can differentiate each individual product in the sum.
(c)
f(b) is a constant so
d/dx(f(b)) = 0 [See
here for Constant Rule]
(d)
d/dx(-f(x)) = -f'(x) [See
here for details]
(e)
d/dx[-f'(x)(b-x)] = -f''(x)(b-x) - f'(x)(-1) = f'(x) -f''(x)(b-x) [See
here for the Product Rule]
(f)
d/dx[(-f''(x)/2!)(b-x)2] = (-f(3)(x)/2!)(b-x)2 + [-f''(x)/2!](2)(b-x)(-1)] == (-f(3)/2!)(b-x)2 + f''(x)(b-x) [See
here for Generalized Power Rule]
(g)
d/dx([-f(n)(x)/n!](b-x)n) = (-f(n+1)(x)/n!)(b-x)n + [-f(n)(n)/n!](n)(b-x)n-1*(-1) == (-f(n+1)(x)/n!)(b-x)n +[ f(n)/(n-1)!](b-x)n-1(h) Since
K is a constant
d/dx(-K(b-x)n+1) = (n+1)(-K)(b-x)n(-1) = (n+1)K(b-x)n(9) We see that most of the terms cancel out so that we get:
g'(x) = (n+1)K(b-x)n - (1/n!)f(n+1)(x)(b-x)n(10) Applying the fact that
g'(z) = 0 from step #7 gives us:
g'(z) = (n+1)K(b-z)n - (1/n!)f(n+1)(z)(b-z)n = 0(11) We can divide both sides by
(b-z)n to get:
(n+1)K - (1/n!)f(n+1)(z) = 0(12) Now we can rearrange (#11) to get:
K = [(1/n!)f(n+1)(z)]/(n+1) = [f(n+1)(z)]/(n+1)!(13) Now, using (#12) and (#3) with
x=a, we get:
g(a) = 0 = f(b) - f(a) - f'(a)(b-a) - [f''(a)/2!](b-a)2 - ... - [f(n)(a)/n!](b-a)n - [(b-a)n+1][f(n+1)(z)/(n+1)!](14) Now, if we move over all the elements after
f(b), we get:
f(b) = f(a) + f'(a)(b-a) + [f''(a)/2!](b-a)2 + ... + [f(n)(a)/n!](b-a)n + [(b-a)n+1][f(n+1)(z)/(n+1)!]QED
References