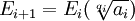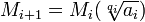The content in today's blog is taken from the essay by Michael I. Rosen entitled "Niels Hendrik Abel and Equations of the Fifth Degree."
In today's blog, I present the key lemma that I will use to establish Step 1 of the proof using field extensions. For the proof using the ideas that
Niels Abel originally presented, see
here.
Lemma 1:Let:
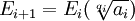
where
qi is prime,
ai ∈ Eiand
Ei, Ei+1 are fields that include the roots of unity
L is a field such that
(Ei ∩ L) ⊂ (Ei+1 ∩ L) ⊂ L and includes the roots of unity.
Mi+1 = Ei+1 ∩ LMi = Ei ∩ Lγ ∈ Mi+1 but not in
MiThen:
There exist:
γi = c0 + c1ζi-1β + c2ζ2(i-1)β2 + ... + cq-1ζ(q-1)(i-1)βq-1such that:
ci ∈ Ei
β ∈ Ei+1, βq ∈ Eiγi ∈ Mi+1ζ is a primitive
qth root of unity
Proof:
(1) From our assumptions, we know that
γq ∈ Mi(2) Let
P(x) be a polynomial such that
P(γ) = 0, that is,
γ is a root for
P(x).
(3) We further know that (see Corollary 3.1,
here) there exists an element
β ∈ Ei+1 such that
βq ∈ Eiand there exists
b0, b2, ..., bq-1 ∈ Ei such that:
γ = b0 + β + b2β2 + ... + bq-1βq-1(4) We can define a function
Q(γ) such that
Q(γ) = P(b0 + x + b2x2 + ... + bq-1xq-1)
(5) From this definition, it is clear that
Q(β) = P(γ) = 0 so that
β is a root for
Q(γ).
(6) Let
a = βq(7) It is clear that
β is the root of
Yq - a.
(8) We also know that
Yq - a is irreducible over
Mi [See Lemma 1,
here]
(9) But since
β is a root for both
Yq - a and
Q(Y), it follows that
Yq - a divides
Q(Y) and every root of
Yq - a is also a root of
Q(Y). [See Theorem 3,
here]
(10) By the Fundamental Theorem of Algebra [See Theorem,
here], we know that there are
q roots for
Yq - a and they are:
&beta, ζβ, ζ2β, ..., ζq-1β where
ζ is a primitive
qth root of unity [see
here for review of the primitive roots of unity].
(11) Since
Yq - a divides
Q(Y) and
ζiβ is a root of
Yq - a, it follows that
Q(ζiβ) = 0 for all integers
i.
(12) So, the numbers [see step #5 above]:
γ = γ1 = b0 + β + b2β2 + ... + bq-1βq-1γ2 = b0 + ζβ + b2ζ2β2 + ... + bq-1ζq-1βq-1...γq = b0 + ζq-1β + b2ζ2(q-1)β2 + ... + bq-1ζ(q-1)(q-1)βq-1are all roots of
P(x). That is,
P(γk) = 0 for
k = 1, ..., q.
(13) We also know that the numbers
γ1, γ2, ..., γq are all in
L since:
(a)
γ ∈ Mi+1 = Ei+1 ∩ L [from step #1 above]
(b) So,
γ ∈ Ei+1 and
γ ∈ L.
(c) Then, using Lemma 5,
here, we can see that each
γk ∈ L.
QED
Lemma 2:Let:
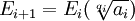
where
qi is prime,
ai ∈ Eiand
Ei, Ei+1 are fields that include the roots of unity
L is a field such that
(Ei ∩ L) ⊂ (Ei+1 ∩ L) ⊂ L and includes the roots of unity.
Mi+1 = Ei+1 ∩ LMi = Ei ∩ LThen:
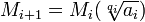
where
qi is prime,
ai ∈ MiProof:
(1) Let
y be an element such that
y ∈ Mi+1 but
y is not an element in
MiWe know that there is at least one such element since
Mi ⊂ Mi+1(2) Using Lemma 1 above, we know that there exists
y1, ..., yq such that each
yi ∈ Mi+1 such that:
y = y1 = b0 + β + b2β2 + ... + bq-1βq-1y2 = b0 + ζβ + b2ζ2β2 + ... + bq-1ζq-1βq-1...yq = b0 + ζq-1β + b2ζ2(q-1)β2 + ... + bq-1ζ(q-1)(q-1)βq-1where
β ∈ Ei+1 but not in
Eiβq ∈ Eib0, ..., bq-1 ∈ Ei(3) Now, if we multiply each equation in step #13 above by
ζ1-i, we get:
y = y1 = b0 + β + b2β2 + ... + bq-1βq-1ζ-1y2 = ζq-1y2 = ζq-1b0 + ζ0β + b2ζ1β2 + ... + bq-1ζq-2βq-1...ζ1-qyq = ζ1 = ζb0 + ζ0β + b2ζ2(q-1)+1β2 + ... + bq-1ζ(q-1)(q-1)+1βq-1(4) If we add up each row, then we have the following values for each column [Using Lemma 4,
here]:
b0 + ζ-1b0 + ... + ζ1-qb0 = b0(1 + ζ1*(q-1) + ζ2*(q-1) + ... + ζ(q-1)*(q-1)) = b0*0 = 0. [Since
q doesn't divide
q-1.]
β + ζ0β + ... + ζ0β = qβb2β2 + ζ1b2β2 + ... + ζq-1b2β2 = b2β2(1 + ζ1*1 + ζ2*1 + ... + ζ(q-1)*1) = b2β2*0 = 0...
bq-1βq-1 + ζq-2bq-1βq-1 + ... + ζ2b2β2 = bq-1βq-1(1 + ζ1*1 + ζ2*1 + ... + ζ(q-1)*1) = bq-1βq-1*0 = 0(5) So, adding each of the columns together gives us the following equation:
β = (1/q)∑ (i=1,q) ζ1-iyi ∈ LWe know that
β ∈ L since all
ζ1-i,q are in
L (by the given) and
yi ∈ L by step #2 above.
(6) Thus
β ∈ L ∩ Ei+1 = Mi+1 and
βq = b ∈ L ∩ E = Mi(7) Let
γ ∈ Mi+1 but not
Mi(8) Then
there exist (see Lemma 1 above using the same value
β as before):
γi = c0 + c1ζi-1β + c2ζ2(i-1)β2 + ... + cq-1ζ(q-1)(i-1)βq-1 with
ci∈ Ei and each
γi ∈ Mi+1(9) If we multiply each
γi by
ζk(1-i) and add up each column in the same way that we did in steps #15 - #17), we get:
ckβk = ∑ (i=1,q) ζk(1-i)γi .
(10) Now since
ζk(1-i), γi ∈ Mi+1, it follows that each
ckβk ∈ Mi+1(11) Since
β ∈ Mi+1 [See step #6 above], it follows that:
βk ∈ Mi+1, and using step #10 above, we get
ck ∈ Mi+1(12) But if
ck ∈ Mi+1 = Ei+1 ∩ L, it follows that
ck ∈ L.
(13) And since
ck ∈ Ei [see step #8 above] and
ck ∈ L [see step #12 above], it follows that
ck ∈ Mi = Ei ∩ L.
(14) Thus, we have show that:
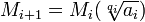
where
qi is prime,
ai ∈ MiQED
Theorem 2: If
E/K is a radical tower and
L ⊆ E, then it follows that
L/K is also a radical tower.
Proof:
(1) Since
E/K is a radical tower, we have (see Definition 4,
here):
K = E0 ⊂ E1 ⊂ E2 ⊂ ... ⊂ Em = Ewhere for each
Ei we have:
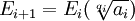
such that:
qi is prime,
ai ∈ Ei(2) Since
K ⊂ L, it follows that:
K = E0 ∩ L(3) Further, since
Ei ⊂ Ei+1, it follows that:
Ei ∩ L ⊆ Ei+1 ∩ L(4) Since
L ⊆ E, it follows that
L = E ∩ L(5) Putting steps #2, #3, and #4 together gives us:
K = (E0 ∩ L) ⊆ (E1 ∩ L) ⊆ ... ⊆ (Em-1 ∩ L) ⊆ L(6) Now, if remove all cases where
Ei ∩ L = Ei+1 ∩ L and renumber, then we get the following:
K = (E0 ∩ L) ⊂ (E1 ∩ L) ⊂ ... ⊂ En = L(7) Using Lemma 2 above, we know that for each
Ei, (Ei+1 ∩ L)/(Ei ∩ L) is a field extension.
(8) Thus, we have shown that
L/K is tower of radicals.
QED
References