In today's blog, I will use the zeta function to answer the question: what are the odds that two integers selected at random are relatively prime.
Lemma 1: The odds that p divides any positive integer selected at random is 1/p
Proof:
(1) Let us assume that we have n integers, that is, the integers 1..n = 1, 2, 3, ..., n. Let x be an integer randomly selected from this list.
(2) If n ≡ 0 (mod p), then it is clear that the odds are 1/p since:
(a) Since p divides n, there exists a value n' such that n = pn'.
(b) So we can divide up n integers in the following way into n' groups of p:
1, ... , p
p+1, ..., 2p
...
n'p-1, ... n'p
(c) We can see that regardless of group n falls in, 1 out of p of those integers in each group are divisible by p.
(3) if n ≡ a (mod p) where a ≠ 0, then we know that p divides n-a so that we have (n-a)=pn'
(4) In this case, we divide up the n integers into n' groups of p just as before but then we are also left with a group of a integers.
1, ..., p
p+1, .. , 2p
...
n'p-1, ..., n'p
n'p+1, ... n'p+a
(5) We can see that there are a total of n' ways to be divisible by p out of a total of n integers. This gives us odds = n'/(n'p+a)
(6) As we increase n toward infinity, we can use L'Hopital's Rule to give us:
lim (n' → ∞) [n'/(n'p + a)]
let f(x) = n'
let g(x) = n'p + a
f'(x) = 1
g'(x) = p
So lim(n' → ∞) [n'/(n'p+a)] = f'(x)/g'(x) = 1/p
QED
Corollary 1.1: The odds that p divides any 2 positive integers selected at random is 1/p2
Proof:
This follows directly from Lemma 1 above. If the odds of p dividing each positive integer is 1/p, the odds of it dividing both are (1/p)(1/p) = 1/p2
QED
Lemma 2: The odds that any 2 positive integers selected at random are relatively prime is 6/π2
Proof:
(1) Let x,y be two positive integers selected at random.
(2) The odds that a prime p divides both is 1/p2 [From the Corollary 1.1 above]
(3) The odds that a prime p fails to divide both is (1 - 1/p2)
(4) Since each prime is distinct, the odds that no prime p divides both = ∏ (p = all primes)(1 - 1/p2)
(5) Now, let's consider the reciprocal of each factor (1 - 1/p2):
1/(1 - 1/p2) = 1/([p2 - 1]/p2) = p2/(p2 - 1)
(6) Now, consider what happens if we multiply to (p2 - 1) to the following sequence S:
Let S = 1 + 1/p2 + 1/p4 + 1/p6 + 1/p8 + ...
(p2 - 1)S = p2 + 1 + 1/p4 + ... - 1 - 1/p2 -1/p4 = p2
So that:
S = p2/(p2 - 1) = 1 + 1/p2 + 1/p4 + ...
(7) Putting this together gives us:
∏ (p = all primes)1/(1 - 1/p2)=∏ (p = all primes)(p2/(p2 - 1) = ∏ (p = all primes) ∑ (n=1,∞) 1/p2(n-1) = (1 + 1/22 + 1/24 + ... )(1 + 1/32 + 1/34 + ...)(1 + 1/52 + 1/54 + ...)*... =
= 1*1*1*1*...*1 + 1/22*1*1*1*...*1 + 1/32*1*1*1*...*1 + 1/52*1*1*1*..*1 + .... + 1/22*1/32*1*..*1 + ...
We note that it equals all combinations of 1/p2.
(8) Applying the Fundamental Theorem of Arithmetic (see here), this gives us:
1*1*1*1*...*1 + 1/22*1*1*1*...*1 + 1/32*1*1*1*...*1 + 1/52*1*1*1*..*1 + .... + 1/22*1/32*1*..*1 + ...
=∑ (n=1,∞) 1/n2
(9) So putting it all together gives us:
∏ (p = all primes)1/(1 - 1/p2) = ∑ (n=1, ∞) 1/n2
(10) But, we know that:
∑ (n=1, ∞) 1/n2 = π2/6 (see here)
(11) Now, taking the reciprocal of this gives us:
∏ (p = all primes)(1 - 1/p2) = 6/π2.
QED
References
Saturday, September 02, 2006
Thursday, August 31, 2006
Sum of the reciprocal of the primes
In today's blog, I will show that the sum of the reciprocal of the primes is divergent, that is, it does not have a limit.
This was first proved by Leonhard Euler. The details in today's blog are based on Euler's original proof.
Lemma 1: ∑ (p=all primes) ∑ (n=2,∞) (p-n)/n is convergent, that is, it has a finite limit.
Proof:
(1) ∑ (p = all primes) ∑ (n=2,∞) (p-n)/n is less than ∑ (p = all primes) ∑ (n=2,∞) (p-n)
This is clear since n is an integer that starts at 2 and goes on until infinity. In each case, we have (p-n) is greater than (p-n)/n
(2) Using the infinite geometric series equation (see Lemma 1, here), we know that:
1 + 1/p + 1/p2 + ... = 1/(1 - 1/p)
(3) Now (1/p2)*[1 + 1/p + 1/p2 + 1/p3 + ... ] = [1/p2 + 1/p3 + ..] so that:
∑ (n=2, ∞) (p-n) = (1/p2)[1/(1 - 1/p)] = 1/[p2(1 - p-1)]
(4) We can then use step #3 to give us:
∑ (p = all primes) ∑ (n=2, ∞) (p-n) = ∑ (p = all primes) 1/[p2(1 - p-1)] =
= ∑ (p = all primes) 1/[(p)(p)(1 - p-1)] =
= ∑ (p = all primes) 1/[(p)(p - 1)]
(5) ∑ (p = all primes) 1/[(p)(p-1)] is less than ∑ (n=2, ∞) 1/[(n)(n-1)] since n includes nonprimes in the sum.
(6) ∑ (n=2, ∞) 1/[(n)(n-1)] = ∑ (n=2,∞) 1/(n2 - n) is less than ∑ (n=2, ∞) 1/(n2 - 2n + 1)
This is true since n2 - 2n + 1 is always less than n2 - n when n ≥ 2.
(7) Since n2 - 2n + 1 = (n-1)2, we have:
∑ (n=2,∞) 1/(n-1)2 = 1 + 1/4 + 1/9 + ... = π2/6 (See Theorem, here)
(8) So, we have now proved that:
∑ (p = all primes) ∑ (n=2,∞) (p-n)/n is less than π2/6 which is finite.
QED
Theorem: Sum of the Reciprocal of Primes is Divergent
∑ 1/p = 1/2 + 1/3 + 1/5 + 1/7 + ... is divergent, that is, does not have a limit.
Proof:
(1) We know that the ζ(1) = harmonic series, that is, ∑ 1/n diverges, that is, the limit of ∑ 1/n approaches infinity. [See Lemma 3, here]
NOTE: ζ(s) is the zeta function which is equal to ∑ 1/ns. So ζ(1) = ∑ 1/n1 = ∑ 1/n.
(2) From step #1, the limit of log(ζ(1)) approaches infinity. This follows directly from step #1 and the fact that as x gets bigger, log x likewise gets bigger. As x heads to infinity, log x also heads to infinity (see here for background on logarithms)
(3) Using Euler's Product Formula (see Theorem 4, here), we know that:
log(ζ(1)) = log(∑ 1/n) = log(∏ (1 - p-1)-1)
NOTE: ∏ (1 - p-1)-1) is a product of all primes p.
(4) By the property of logarithms (see here), we have:
log(∏ (1 - p-1)-1) = ∑ log([1 - p-1]-1) = ∑ -log(1 - p-1)
(5) Now using some basic properties of the integral (see Theorem, here), we have:
log (1 + x) = ∑ (n=1,∞) [(-1)n+1xn]/n
Let x = -p-1
Then we have:
log (1 + [-p-1]) = ∑ [(-1)n+1(-p-1)n]/n = ∑ [(-1)n+1(-1)n(p-1)n]/n =
= ∑ [(-1)2n+1(p-n)]/n
Since 2n+1 is always odd, this gives us:
log(1 + [-p-1]) = ∑ -(p-n)/n
Since p-n/n is always positive, we have ∑ -(p-n)/n = (-1)∑ (p-n)/n
Further,
-log(1 + [-p-1]) = (-1)log(1 + [-p-1]) = (-1)(-1)∑ (p-n)/n = ∑ (p-n)/n
(6) Combining step #5 with step #4 gives us:
∑ -log(1 - p-1) = ∑ (p=all primes) ∑ (n=1,∞) (p-n)/n
(7) ∑ (p=all primes) ∑ (n=1,∞) (p-n)/n=∑(p=all primes) 1/p + ∑ ∑ (n=2,∞) (p-n)/n
(8) Using Lemma 1 above, we know that ∑ ∑ (n=2,∞) (p-n)/n is convergent, that is, it has a finite limit.
(9) But from step #2, we know that ∑ 1/p + ∑ ∑ (n=2, ∞) (p-n)/n has a limit of infinity.
(10) Therefore, it follows, that ∑ 1/p must be divergent, that is, it must have a limit of infinity.
QED
References
This was first proved by Leonhard Euler. The details in today's blog are based on Euler's original proof.
Lemma 1: ∑ (p=all primes) ∑ (n=2,∞) (p-n)/n is convergent, that is, it has a finite limit.
Proof:
(1) ∑ (p = all primes) ∑ (n=2,∞) (p-n)/n is less than ∑ (p = all primes) ∑ (n=2,∞) (p-n)
This is clear since n is an integer that starts at 2 and goes on until infinity. In each case, we have (p-n) is greater than (p-n)/n
(2) Using the infinite geometric series equation (see Lemma 1, here), we know that:
1 + 1/p + 1/p2 + ... = 1/(1 - 1/p)
(3) Now (1/p2)*[1 + 1/p + 1/p2 + 1/p3 + ... ] = [1/p2 + 1/p3 + ..] so that:
∑ (n=2, ∞) (p-n) = (1/p2)[1/(1 - 1/p)] = 1/[p2(1 - p-1)]
(4) We can then use step #3 to give us:
∑ (p = all primes) ∑ (n=2, ∞) (p-n) = ∑ (p = all primes) 1/[p2(1 - p-1)] =
= ∑ (p = all primes) 1/[(p)(p)(1 - p-1)] =
= ∑ (p = all primes) 1/[(p)(p - 1)]
(5) ∑ (p = all primes) 1/[(p)(p-1)] is less than ∑ (n=2, ∞) 1/[(n)(n-1)] since n includes nonprimes in the sum.
(6) ∑ (n=2, ∞) 1/[(n)(n-1)] = ∑ (n=2,∞) 1/(n2 - n) is less than ∑ (n=2, ∞) 1/(n2 - 2n + 1)
This is true since n2 - 2n + 1 is always less than n2 - n when n ≥ 2.
(7) Since n2 - 2n + 1 = (n-1)2, we have:
∑ (n=2,∞) 1/(n-1)2 = 1 + 1/4 + 1/9 + ... = π2/6 (See Theorem, here)
(8) So, we have now proved that:
∑ (p = all primes) ∑ (n=2,∞) (p-n)/n is less than π2/6 which is finite.
QED
Theorem: Sum of the Reciprocal of Primes is Divergent
∑ 1/p = 1/2 + 1/3 + 1/5 + 1/7 + ... is divergent, that is, does not have a limit.
Proof:
(1) We know that the ζ(1) = harmonic series, that is, ∑ 1/n diverges, that is, the limit of ∑ 1/n approaches infinity. [See Lemma 3, here]
NOTE: ζ(s) is the zeta function which is equal to ∑ 1/ns. So ζ(1) = ∑ 1/n1 = ∑ 1/n.
(2) From step #1, the limit of log(ζ(1)) approaches infinity. This follows directly from step #1 and the fact that as x gets bigger, log x likewise gets bigger. As x heads to infinity, log x also heads to infinity (see here for background on logarithms)
(3) Using Euler's Product Formula (see Theorem 4, here), we know that:
log(ζ(1)) = log(∑ 1/n) = log(∏ (1 - p-1)-1)
NOTE: ∏ (1 - p-1)-1) is a product of all primes p.
(4) By the property of logarithms (see here), we have:
log(∏ (1 - p-1)-1) = ∑ log([1 - p-1]-1) = ∑ -log(1 - p-1)
(5) Now using some basic properties of the integral (see Theorem, here), we have:
log (1 + x) = ∑ (n=1,∞) [(-1)n+1xn]/n
Let x = -p-1
Then we have:
log (1 + [-p-1]) = ∑ [(-1)n+1(-p-1)n]/n = ∑ [(-1)n+1(-1)n(p-1)n]/n =
= ∑ [(-1)2n+1(p-n)]/n
Since 2n+1 is always odd, this gives us:
log(1 + [-p-1]) = ∑ -(p-n)/n
Since p-n/n is always positive, we have ∑ -(p-n)/n = (-1)∑ (p-n)/n
Further,
-log(1 + [-p-1]) = (-1)log(1 + [-p-1]) = (-1)(-1)∑ (p-n)/n = ∑ (p-n)/n
(6) Combining step #5 with step #4 gives us:
∑ -log(1 - p-1) = ∑ (p=all primes) ∑ (n=1,∞) (p-n)/n
(7) ∑ (p=all primes) ∑ (n=1,∞) (p-n)/n=∑(p=all primes) 1/p + ∑ ∑ (n=2,∞) (p-n)/n
(8) Using Lemma 1 above, we know that ∑ ∑ (n=2,∞) (p-n)/n is convergent, that is, it has a finite limit.
(9) But from step #2, we know that ∑ 1/p + ∑ ∑ (n=2, ∞) (p-n)/n has a limit of infinity.
(10) Therefore, it follows, that ∑ 1/p must be divergent, that is, it must have a limit of infinity.
QED
References
- Jay R. Goldman, The Queen of Mathematics, A K Peters, 1998
- Proof that the Sum of the Reciprocals of Primes Diverge, Wikipedia
- Natural Logarithm, Wikipedia
Monday, August 28, 2006
∑ 1/n2 = π2/6
In today's blog, I show the proof that ∑ 1/n2 = π2/6. For background on Basel's problem and Leonhard Euler's technique for arriving at the solution, see here. In today's blog, I show a proof that Euler's solution is correct.
Most of the content in today's blog is taken from the Wikipedia article on the Basel Problem. See references below for more information.
Lemma 1: cot2(x) is one-to-one on the interval (0,π/2)
Proof:
(1) Suppose there exists x,y such that cot2(x) = cot2(y) in the interval (0,π/2)
(2) By definition, cot(x) = (cos x)/(sin x) so that we have:
(cos2 x)/(sin2 x) = (cos2 y)/(sin2 y)
which means that:
(cos2 x)/(cos2 y) = (sin2 x)/(sin2 y)
(3) We also know (see Corollary 2, here), cos2(x) + sin2(x) = 1 which is the same as:
1 - sin2(x) = cos2(x)
(4) Now, we can make the same argument for y and then we can divide by y to get:
[1 - sin2(x)]/[1 - sin2(y)] = [cos2(x)]/[cos2(y)]
(5) Now, we can substitute in step #2 to give us:
[1 - sin2(x)]/[1 - sin2(y)] = (sin2 x)/(sin2 y)
(6) This amounts to:
(sin2 y)(1 - sin2 x) = (sin2 x)(1 - sin2 y)
(7) Adding (sin2 x)(sin2 y) to both sides gives us:
(sin2 y)(1 - sin2 x) + (sin2 x)(sin2 y) =
= (sin2 y)(1 - sin2 x + sin2 x) = sin2 y
(sin2x)(1 - sin2 y) + (sin2 x)(sin2 y) =
= (sin2x)(1 - sin2y + sin2 y) = sin2 x
So that we have:
sin2 y = sin2 x
(8) Squaring both sides gives us:
±(sin y) = ±(sin x)
(9) Since we know that the sin function is nonnegative on the interval (0, π/2), we know that the square has to be nonnegative. This gives us:
sin y = sin x
(10) Finally, since sin x is one-to-one on the interval (0,π/2) (see here for properties of sin), we can see that x = y.
The basic idea here is that the sin function between 0 and π/2 does not repeat any of its values. This proves that if sin x = sin y, then x = y.
QED
Lemma 2: Sum of coefficients for a polynomial
if :
f(t) = amtm + am-1tm-1 + ... + a1t + a0 where am ≠ 0
then:
the sum of the roots of f(t) [counting multiplicities] is -am-1/am
Proof:
(1) Using the Fundamental Theorem of Algebra (see here), we know that we can divide up f(t) into a sequence of m roots such that:
f(t) = am(t - r1)(t - r2)*...*(t - rm)
(2) Now when we multiply all these values together it is clear that the sum of coefficients for tm-1 = the sum of all the roots multiplied by am.
We can see that if we carry out the multiplication of (t - r1)(t - r2)*...*(t - rm), we get:
tm + tm-1(-r1 + -r2 + ... + -rm) + ... + (-r1)(-r2)*...*(-rm)
(3) We can see that the coefficient for tm-1, am-1 = -am(r1 + r2 + ... + rm)
(4) But then r1 + r2 + ... + rm = -am-1/am
QED
Lemma 3: csc2(x) = 1 + cot2(x)
Proof:
(1) sin2x + cos2x = 1 (see Corollary 2, here)
(2) Divide both sides by sin2
Then we have:
1/(sin2x) = 1 + (cos2x)/(sin2x)
(3) Since by definition, cot2x = (cos2 x)/(sin2 x) and csc2x = 1/(sin2x), step #2 gives us:
csc2 x = 1 + cot2 x
QED
Lemma 4: cot2x is less than 1/x2 which is less than csc2 x on the interval (0,π/2)
Proof:
(1) If x is in (0, π/2), then (see Theorem, here):
sin x is less than x which is less than tan x.
(2) Taking the inverse of each (since x ≠ 0 → sin x ≠ 0 and tan x ≠ 0) gives us:
csc x is greater than 1/x which is greater than cot x.
(3) Now, squaring each value gives us:
cot2 x is less than 1/x2 which is less than csc2 x.
QED
Lemma 5: as m approaches infinity, both (2m)(2m+2)/(2m+1)2 and (2m)(2m-1)/(2m+1)2 approaches 1
Proof:
(1) Putting all values into polynomial form, we have:
(2m)(2m+2) = 4m2 + 4m
(2m)(2m - 1) = 4m2 - 2m
(2m+1)2 = 4m2 + 4m + 1
(2) Now, we can calculate the limits using L'Hopital's rule (see here)
lim (m → ∞) [(4m2 - 2m)/(4m2 + 4m + 1)] = lim (m → ∞) [(8m - 2)/(8m + 4)] = lim (m → ∞) [8/8] = 1.
lim (m → ∞) [(4m2 + 4m)/(4m2 + 4m + 1)] = lim (m → ∞) [(8m + 4)/(8m + 4)] = 1.
QED
Theorem: ∑ 1/n2 = π2/6
Proof:
(1) Using De Moivre's Formula (see Corollary, here for proof) we know that:
(cos x + i sin x)n = cos(nx) + i sin(nx)
(2) Dividing both sides by (sin x)n gives us:
[cos(nx) + i sin(nx)]/(sin x)n = (cos x + i sin x)n/(sin x)n = [(cos x + i sin x)/sin x]n
(3) Since cot x = (cos x)/(sin x) [by definition, cot(x) = 1/tan(x)], we have:
[(cos x + i sin x)/sin x] = cot x + i
(4) Putting this all together gives us:
[ cos(nx) + i sin(nx) ]/(sin x)n = (cot x + i)n
(5) Using the Binomial Theorem [See here], we know that:
(cot x + i)n = cotn x + (n,1)(cotn-1x)i + ... + (n,n-1)(cot x)in-1 + in
(6) Since i2 = -1, we can now divide up all terms in step #5 so that we have:
cotn x + (n,1)(cotn-1x)i + ... + (n,n-1)(cot x)in-1 + in = [(cotnx) - (n,2)(cotn-2 x) ± ... ] + i[(n,1)(cotn-1x) - (n,3)(cotn-3x) ± ... ]
(7) Since for any identity a + bi = c + di, we know that a=c and b=d, we can build the following equation from step #2 and step #6:
[isin(nx)]/(sin x)n = i[(n,1)(cotn-1x) - (n,3)(cotn-3x) ± ... ]
(8) Dividing both sides by i gives us:
sin(nx)/(sin x)n = [(n,1)(cotn-1x) - (n,3)(cotn-3x) ± ... ]
(9) Now, since step #8 is an identity, it is true for all values n,x.
Let n = 2m + 1 where m is a positive integer.
Let x = rπ/(2m + 1) where r can = 1, 2, ..., m
From this, we can see that:
nx = (2m + 1)*(rπ)/(2m+1) = rπ
(10) From a property of sin (see Lemma 1, here), we can see that:
sin(nx) =0
(11) Applying these values to step #8 gives us:
sin(nx)/(sin x)n = 0/(sin x)n = 0 =
= [(n,1)(cotn-1x) - (n,3)(cotn-3x) ± ... ] =
= [(2m+1,1)(cot2mx) - (2m+1,3)(cot2m-2x) ± ... + (-1)m ]
(12) Using Lemma 1 above, we can conclude that the values for x in step #11 are distinct. By the above equation we know that each of these m distinct solutions for x are roots to the following equation:
(2m + 1, 1)tm - (2m + 1,3)tm-1 ± ... + (-1)m = 0
(13) Using Lemma 2 to calculate the sum of roots using the coefficients, we have:
cot2(π/[2m+1]) + cot2(2π/[2m + 1]) + ... + cot2(mπ/[2m + 1]) = (2m+1,3)/(2m+1,1) = [(2m+1)!/(2m-2)!(3!)]/[(2m+1)!/(2m)!] = [(2m+1)(2m)(2m-1)/6]/(2m+1)] = (2m)(2m-1)/6.
(14) Using Lemma 3 above, we know that:
csc2 x = cot2x + 1
which means that:
cot2x = csc2 x - 1
(15) Applying (cot2x = csc2x - 1) to step #13 gives us:
cot2(π/[2m+1]) + cot2(2π/[2m + 1]) + ... + cot2(mπ/[2m + 1]) =
csc2(π/[2m+1]) + csc2(2π/[2m + 1]) + ... + csc2(mπ/[2m + 1]) - m =
= (2m)(2m-1)/6.
(16) If we add m to both sides we get:
csc2(π/[2m+1]) + csc2(2π/[2m + 1]) + ... + csc2(mπ/[2m + 1]) = (2m)(2m-1)/6 + m = (2m)(2m-1)/6 + 6m/6 = (4m2 - 2m + 6m)/6 = (4m2 + 4m)/6 = (2m)(2m+2)/6
(17) From Lemma 4 above, we know that for the interval (0,π/2) we have the following inequality:
cot2x is less than 1/x2 which is less than csc2 x
(18) But this implies that:
cot2(π/[2m+1]) + cot2(2π/[2m + 1]) + ... + cot2(mπ/[2m + 1]) is less than ([2m+1]/π)2 + ([2m+1]/2π)2 + ... + ([2m+1]/mπ)2 which is less than csc2(π/[2m+1]) + csc2(2π/[2m + 1]) + ... + csc2(mπ/[2m + 1])
(19) Now since we know that
(a) cot2(π/[2m+1]) + cot2(2π/[2m + 1]) + ... + cot2(mπ/[2m + 1]) = (2m)(2m-1)/6
(b) csc2(π/[2m+1]) + csc2(2π/[2m + 1]) + ... + csc2(mπ/[2m + 1]) = (2m)(2m+2)/6
We have:
(2m)(2m-1)/6 is less than ([2m+1]/π)2 + ([2m+1]/2π)2 + ... + ([2m+1]/mπ)2 which is less than (2m)(2m+2)/6
(20) If we multiply on all sides by (π/(2m+1))2, then we have:
π2/(2m+1)2(2m)(2m-1)/6 = (π2)(2m)(2m-1)/(6)(2m+1)2
(π2)/(2m+1)2([2m+1]/π)2 + ([2m+1]/2π)2 + ... + ([2m+1]/mπ)2 = 1/1 + 1/4 + .. + 1/m2
(π2)/(2m+1)2(2m)(2m+2)/6 = π2(2m)(2m-1)/(6)(2m+1)2
(21) By Lemma 5 above, as m approaches infinity, both the left and right hand expressions approach (π2)/6 so by the Squeeze Theorem (see Lemma 3, here for proof), we have:
∑ (k=1,∞) (1/k2) = lim (m → ∞) (1/12 + 1/22 + ... + 1/m2) = π2/6
QED
References
Most of the content in today's blog is taken from the Wikipedia article on the Basel Problem. See references below for more information.
Lemma 1: cot2(x) is one-to-one on the interval (0,π/2)
Proof:
(1) Suppose there exists x,y such that cot2(x) = cot2(y) in the interval (0,π/2)
(2) By definition, cot(x) = (cos x)/(sin x) so that we have:
(cos2 x)/(sin2 x) = (cos2 y)/(sin2 y)
which means that:
(cos2 x)/(cos2 y) = (sin2 x)/(sin2 y)
(3) We also know (see Corollary 2, here), cos2(x) + sin2(x) = 1 which is the same as:
1 - sin2(x) = cos2(x)
(4) Now, we can make the same argument for y and then we can divide by y to get:
[1 - sin2(x)]/[1 - sin2(y)] = [cos2(x)]/[cos2(y)]
(5) Now, we can substitute in step #2 to give us:
[1 - sin2(x)]/[1 - sin2(y)] = (sin2 x)/(sin2 y)
(6) This amounts to:
(sin2 y)(1 - sin2 x) = (sin2 x)(1 - sin2 y)
(7) Adding (sin2 x)(sin2 y) to both sides gives us:
(sin2 y)(1 - sin2 x) + (sin2 x)(sin2 y) =
= (sin2 y)(1 - sin2 x + sin2 x) = sin2 y
(sin2x)(1 - sin2 y) + (sin2 x)(sin2 y) =
= (sin2x)(1 - sin2y + sin2 y) = sin2 x
So that we have:
sin2 y = sin2 x
(8) Squaring both sides gives us:
±(sin y) = ±(sin x)
(9) Since we know that the sin function is nonnegative on the interval (0, π/2), we know that the square has to be nonnegative. This gives us:
sin y = sin x
(10) Finally, since sin x is one-to-one on the interval (0,π/2) (see here for properties of sin), we can see that x = y.
The basic idea here is that the sin function between 0 and π/2 does not repeat any of its values. This proves that if sin x = sin y, then x = y.
QED
Lemma 2: Sum of coefficients for a polynomial
if :
f(t) = amtm + am-1tm-1 + ... + a1t + a0 where am ≠ 0
then:
the sum of the roots of f(t) [counting multiplicities] is -am-1/am
Proof:
(1) Using the Fundamental Theorem of Algebra (see here), we know that we can divide up f(t) into a sequence of m roots such that:
f(t) = am(t - r1)(t - r2)*...*(t - rm)
(2) Now when we multiply all these values together it is clear that the sum of coefficients for tm-1 = the sum of all the roots multiplied by am.
We can see that if we carry out the multiplication of (t - r1)(t - r2)*...*(t - rm), we get:
tm + tm-1(-r1 + -r2 + ... + -rm) + ... + (-r1)(-r2)*...*(-rm)
(3) We can see that the coefficient for tm-1, am-1 = -am(r1 + r2 + ... + rm)
(4) But then r1 + r2 + ... + rm = -am-1/am
QED
Lemma 3: csc2(x) = 1 + cot2(x)
Proof:
(1) sin2x + cos2x = 1 (see Corollary 2, here)
(2) Divide both sides by sin2
Then we have:
1/(sin2x) = 1 + (cos2x)/(sin2x)
(3) Since by definition, cot2x = (cos2 x)/(sin2 x) and csc2x = 1/(sin2x), step #2 gives us:
csc2 x = 1 + cot2 x
QED
Lemma 4: cot2x is less than 1/x2 which is less than csc2 x on the interval (0,π/2)
Proof:
(1) If x is in (0, π/2), then (see Theorem, here):
sin x is less than x which is less than tan x.
(2) Taking the inverse of each (since x ≠ 0 → sin x ≠ 0 and tan x ≠ 0) gives us:
csc x is greater than 1/x which is greater than cot x.
(3) Now, squaring each value gives us:
cot2 x is less than 1/x2 which is less than csc2 x.
QED
Lemma 5: as m approaches infinity, both (2m)(2m+2)/(2m+1)2 and (2m)(2m-1)/(2m+1)2 approaches 1
Proof:
(1) Putting all values into polynomial form, we have:
(2m)(2m+2) = 4m2 + 4m
(2m)(2m - 1) = 4m2 - 2m
(2m+1)2 = 4m2 + 4m + 1
(2) Now, we can calculate the limits using L'Hopital's rule (see here)
lim (m → ∞) [(4m2 - 2m)/(4m2 + 4m + 1)] = lim (m → ∞) [(8m - 2)/(8m + 4)] = lim (m → ∞) [8/8] = 1.
lim (m → ∞) [(4m2 + 4m)/(4m2 + 4m + 1)] = lim (m → ∞) [(8m + 4)/(8m + 4)] = 1.
QED
Theorem: ∑ 1/n2 = π2/6
Proof:
(1) Using De Moivre's Formula (see Corollary, here for proof) we know that:
(cos x + i sin x)n = cos(nx) + i sin(nx)
(2) Dividing both sides by (sin x)n gives us:
[cos(nx) + i sin(nx)]/(sin x)n = (cos x + i sin x)n/(sin x)n = [(cos x + i sin x)/sin x]n
(3) Since cot x = (cos x)/(sin x) [by definition, cot(x) = 1/tan(x)], we have:
[(cos x + i sin x)/sin x] = cot x + i
(4) Putting this all together gives us:
[ cos(nx) + i sin(nx) ]/(sin x)n = (cot x + i)n
(5) Using the Binomial Theorem [See here], we know that:
(cot x + i)n = cotn x + (n,1)(cotn-1x)i + ... + (n,n-1)(cot x)in-1 + in
(6) Since i2 = -1, we can now divide up all terms in step #5 so that we have:
cotn x + (n,1)(cotn-1x)i + ... + (n,n-1)(cot x)in-1 + in = [(cotnx) - (n,2)(cotn-2 x) ± ... ] + i[(n,1)(cotn-1x) - (n,3)(cotn-3x) ± ... ]
(7) Since for any identity a + bi = c + di, we know that a=c and b=d, we can build the following equation from step #2 and step #6:
[isin(nx)]/(sin x)n = i[(n,1)(cotn-1x) - (n,3)(cotn-3x) ± ... ]
(8) Dividing both sides by i gives us:
sin(nx)/(sin x)n = [(n,1)(cotn-1x) - (n,3)(cotn-3x) ± ... ]
(9) Now, since step #8 is an identity, it is true for all values n,x.
Let n = 2m + 1 where m is a positive integer.
Let x = rπ/(2m + 1) where r can = 1, 2, ..., m
From this, we can see that:
nx = (2m + 1)*(rπ)/(2m+1) = rπ
(10) From a property of sin (see Lemma 1, here), we can see that:
sin(nx) =0
(11) Applying these values to step #8 gives us:
sin(nx)/(sin x)n = 0/(sin x)n = 0 =
= [(n,1)(cotn-1x) - (n,3)(cotn-3x) ± ... ] =
= [(2m+1,1)(cot2mx) - (2m+1,3)(cot2m-2x) ± ... + (-1)m ]
(12) Using Lemma 1 above, we can conclude that the values for x in step #11 are distinct. By the above equation we know that each of these m distinct solutions for x are roots to the following equation:
(2m + 1, 1)tm - (2m + 1,3)tm-1 ± ... + (-1)m = 0
(13) Using Lemma 2 to calculate the sum of roots using the coefficients, we have:
cot2(π/[2m+1]) + cot2(2π/[2m + 1]) + ... + cot2(mπ/[2m + 1]) = (2m+1,3)/(2m+1,1) = [(2m+1)!/(2m-2)!(3!)]/[(2m+1)!/(2m)!] = [(2m+1)(2m)(2m-1)/6]/(2m+1)] = (2m)(2m-1)/6.
(14) Using Lemma 3 above, we know that:
csc2 x = cot2x + 1
which means that:
cot2x = csc2 x - 1
(15) Applying (cot2x = csc2x - 1) to step #13 gives us:
cot2(π/[2m+1]) + cot2(2π/[2m + 1]) + ... + cot2(mπ/[2m + 1]) =
csc2(π/[2m+1]) + csc2(2π/[2m + 1]) + ... + csc2(mπ/[2m + 1]) - m =
= (2m)(2m-1)/6.
(16) If we add m to both sides we get:
csc2(π/[2m+1]) + csc2(2π/[2m + 1]) + ... + csc2(mπ/[2m + 1]) = (2m)(2m-1)/6 + m = (2m)(2m-1)/6 + 6m/6 = (4m2 - 2m + 6m)/6 = (4m2 + 4m)/6 = (2m)(2m+2)/6
(17) From Lemma 4 above, we know that for the interval (0,π/2) we have the following inequality:
cot2x is less than 1/x2 which is less than csc2 x
(18) But this implies that:
cot2(π/[2m+1]) + cot2(2π/[2m + 1]) + ... + cot2(mπ/[2m + 1]) is less than ([2m+1]/π)2 + ([2m+1]/2π)2 + ... + ([2m+1]/mπ)2 which is less than csc2(π/[2m+1]) + csc2(2π/[2m + 1]) + ... + csc2(mπ/[2m + 1])
(19) Now since we know that
(a) cot2(π/[2m+1]) + cot2(2π/[2m + 1]) + ... + cot2(mπ/[2m + 1]) = (2m)(2m-1)/6
(b) csc2(π/[2m+1]) + csc2(2π/[2m + 1]) + ... + csc2(mπ/[2m + 1]) = (2m)(2m+2)/6
We have:
(2m)(2m-1)/6 is less than ([2m+1]/π)2 + ([2m+1]/2π)2 + ... + ([2m+1]/mπ)2 which is less than (2m)(2m+2)/6
(20) If we multiply on all sides by (π/(2m+1))2, then we have:
π2/(2m+1)2(2m)(2m-1)/6 = (π2)(2m)(2m-1)/(6)(2m+1)2
(π2)/(2m+1)2([2m+1]/π)2 + ([2m+1]/2π)2 + ... + ([2m+1]/mπ)2 = 1/1 + 1/4 + .. + 1/m2
(π2)/(2m+1)2(2m)(2m+2)/6 = π2(2m)(2m-1)/(6)(2m+1)2
(21) By Lemma 5 above, as m approaches infinity, both the left and right hand expressions approach (π2)/6 so by the Squeeze Theorem (see Lemma 3, here for proof), we have:
∑ (k=1,∞) (1/k2) = lim (m → ∞) (1/12 + 1/22 + ... + 1/m2) = π2/6
QED
References
- Basel Problem, Wikipedia
Sunday, August 27, 2006
The Basel Problem
Leonhard Euler first gained fame by his solution to what has been called the Basel Problem (named after Basel, Switzerland where the problem gained its notoriety). This is the resolution of the infinite sum:
∑ 1/(n2)
The problem had first been posed in 1644 by Pietro Mengoli. The problem was popularized by the celebrated mathematician Jakob Bernoulli in 1689. John Wallis calculated its value of its first three decimals (1.645...). The great Gottfriend von Leibnitz was unable to solve it. Johann Bernoulli, the younger brother of Jakob, also worked on it and failed to solve it.
By the 1730s the problem had gained a mystique as the greatest mathematicians of the age seemed unable to solve it. Then, in 1735, when he was 28, Euler announced that he had found a solution. At first, Euler succeeded in calculating the sum to six decimal places and then later, he reached his very insightful conclusion:
∑ 1/(n2) = π2/6
In today's blog, I will show the steps that Euler followed to arrive at this amazing result. This will not be a proof. Euler purposely made assumptions that enabled him to simplify the problem but which prevented his solution from rising to the level of a proof.
Solution: Euler's solution to the Basel Problem
∑ 1/(n2) = π2/6
(1) Using the Taylor expansion for sin x, we know that (see Lemma 3, here for details)
sin x = x - (x3/3!) + (x5/5!) - (x7/7!) + ...
(2) We know that sin x = 0 in the case where x = 0, ±π, ±2π, ±3π ... (see Lemma 1, here for details).
(3) Using the Fundamental Theorem of Algebra, we get:
x - (x3/3!) + (x5/5!) - (x7/7!) + ... = C(x)(x - π)(x + π)(x - 2π)(x + 2π)(x - 3π)(x + 3π)*... where C is a constant.
(4) Since for each value of π we have a pair: π and -π, we can multiply each of these pairs together to get:
x - (x3/3!) + (x5/5!) - (x7/7!) + ... = C(x)(x2 - π2)(x2 - 4π2)(x2 - 9π2)*...
(5) Since each of these x2 - nπ2 = 0, we can rearrange each to a form of (1 - x2/(nπ2) [See Corollary 1.1, here] so that we have:
x - (x3/3!) + (x5/5!) - (x7/7!) + ... = C(x)(1 - x2/π2)(1 - x2/4π2)(1 - x2/9π2)*...
(6) Now, if we divide each side by x, we get:
(sin x)/x = 1 - (x2/3!) + (x4/5!) - (x6/7!) + ... = C(1 - x2/π2)(1 - x2/4π2)(1 - x2/9π2)*...
(7) Now, since (sin x)/x = 1 as x approaches 0 (see Lemma 2, here), we see that C = 1
Here's why:
As x approaches 0, we have, C(1 - x2/π2)(1 - x2/4π2)(1 - x2/9π2)*... = C(1 - 0)(1 - 0)(1 -0)*... = C
Since sin(x)/x = 1, we can see that C = 1.
(8) So, we are left now with:
1 - (x2/3!) + (x4/5!) - (x6/7!) + ... = (1 - x2/π2)(1 - x2/4π2)(1 - x2/9π2)*...
(9) Now, in mathematics:
if we an identity (that is, an equation that is true for all cases of x):
a0 + a1x + a2x2 + ... anxn = b0 + b1x + b2x2 + ... + bnxn
then:
ai = bi
This means that we can take any power of x and the two sides must be equal.
(10) At this point, Euler took the factor x2 which gives us:
-(x2)/3! = -x2/π2 - x2/4π2 - x2/9π2 - ...
(11) Dividing -x2/π2 from both sides gives us:
π2/6 = 1 + 1/4 + 1/9 + ...
Euler would later publish a more thorough proof of his solution. See here for a proof that ∑ (1/n2) = π2/6.
References
∑ 1/(n2)
The problem had first been posed in 1644 by Pietro Mengoli. The problem was popularized by the celebrated mathematician Jakob Bernoulli in 1689. John Wallis calculated its value of its first three decimals (1.645...). The great Gottfriend von Leibnitz was unable to solve it. Johann Bernoulli, the younger brother of Jakob, also worked on it and failed to solve it.
By the 1730s the problem had gained a mystique as the greatest mathematicians of the age seemed unable to solve it. Then, in 1735, when he was 28, Euler announced that he had found a solution. At first, Euler succeeded in calculating the sum to six decimal places and then later, he reached his very insightful conclusion:
∑ 1/(n2) = π2/6
In today's blog, I will show the steps that Euler followed to arrive at this amazing result. This will not be a proof. Euler purposely made assumptions that enabled him to simplify the problem but which prevented his solution from rising to the level of a proof.
Solution: Euler's solution to the Basel Problem
∑ 1/(n2) = π2/6
(1) Using the Taylor expansion for sin x, we know that (see Lemma 3, here for details)
sin x = x - (x3/3!) + (x5/5!) - (x7/7!) + ...
(2) We know that sin x = 0 in the case where x = 0, ±π, ±2π, ±3π ... (see Lemma 1, here for details).
(3) Using the Fundamental Theorem of Algebra, we get:
x - (x3/3!) + (x5/5!) - (x7/7!) + ... = C(x)(x - π)(x + π)(x - 2π)(x + 2π)(x - 3π)(x + 3π)*... where C is a constant.
(4) Since for each value of π we have a pair: π and -π, we can multiply each of these pairs together to get:
x - (x3/3!) + (x5/5!) - (x7/7!) + ... = C(x)(x2 - π2)(x2 - 4π2)(x2 - 9π2)*...
(5) Since each of these x2 - nπ2 = 0, we can rearrange each to a form of (1 - x2/(nπ2) [See Corollary 1.1, here] so that we have:
x - (x3/3!) + (x5/5!) - (x7/7!) + ... = C(x)(1 - x2/π2)(1 - x2/4π2)(1 - x2/9π2)*...
(6) Now, if we divide each side by x, we get:
(sin x)/x = 1 - (x2/3!) + (x4/5!) - (x6/7!) + ... = C(1 - x2/π2)(1 - x2/4π2)(1 - x2/9π2)*...
(7) Now, since (sin x)/x = 1 as x approaches 0 (see Lemma 2, here), we see that C = 1
Here's why:
As x approaches 0, we have, C(1 - x2/π2)(1 - x2/4π2)(1 - x2/9π2)*... = C(1 - 0)(1 - 0)(1 -0)*... = C
Since sin(x)/x = 1, we can see that C = 1.
(8) So, we are left now with:
1 - (x2/3!) + (x4/5!) - (x6/7!) + ... = (1 - x2/π2)(1 - x2/4π2)(1 - x2/9π2)*...
(9) Now, in mathematics:
if we an identity (that is, an equation that is true for all cases of x):
a0 + a1x + a2x2 + ... anxn = b0 + b1x + b2x2 + ... + bnxn
then:
ai = bi
This means that we can take any power of x and the two sides must be equal.
(10) At this point, Euler took the factor x2 which gives us:
-(x2)/3! = -x2/π2 - x2/4π2 - x2/9π2 - ...
(11) Dividing -x2/π2 from both sides gives us:
π2/6 = 1 + 1/4 + 1/9 + ...
Euler would later publish a more thorough proof of his solution. See here for a proof that ∑ (1/n2) = π2/6.
References
- Julian Havil, Gamma: Exploring Euler's Constant, Princeton University Press, 2003
- Jay R. Goldman, The Queen of Mathematics, AK Peters, Ltd., 1998
- G. Polya, Induction and Analogy in Mathematics, Princeton University Press, 1954.
Saturday, August 26, 2006
Euler Product Formula
One of the major breakthroughs in Analytic Number Theory came with Leonhard Euler's Product Formula (see Theorem 4 below). Associated with this result is the Riemann zeta function which is the foundation of perhaps the most important unsolved mathematical problem in number theory today, the Riemann Hypothesis.
One might ask if Leonhard Euler came up with the zeta function why is it commonly called the Riemann Zeta Function. The answer has to do with the development of the function. While it is true that Euler discovered it, he used it with integer values. Johann Dirichlet would later extend it to real numbers, and Bernhard Riemann extended it to complex numbers. The most interesting properties stem from the complex numbers so it makes sense that it is currently named the Riemann zeta function (see Ed Sandifer's article for details).
So, how did Euler come up with the Euler Product Formula? The Harmonic Series was shown to be divergent (have an infinite sum) by Nicolas Oresme in the 1300s (this is considered one of the high points of mathematics in the middle ages, see Lemma 3 below). Euler wondered if the prime harmonic series (1 + 1/2 + 1/3 + 1/5 + ...) was also divergent. He then began studying the zeta function ζ(s) where:
ζ(s) = 1 + (1/2s) + (1/3s) + ...
For Euler, s is an integer. It turns out that when s=1, ζ(s) = the harmonic series and is therefore divergent. When s ≠ 1, it turns out the the zeta function is convergent, that is, it has a finite limit. In this way, Euler came up with his Product Formula. He then used this result to show that there are an infinitude of primes and the prime harmonic series is infinite. Unfortunately, while his conclusion about the prime harmonic series is correct, his proof today is not considered valid (see Ed Sandier's article for more information). See here for details on the proof for the divergence of the prime harmonic series.
Lemma 1: Infinite Geometric Series
if x ≠ 1, then:
1/(1-x) = 1 + x + x2 + x3 + ... + xn
Proof:
(1) Let s = 1 + x + x2 + x3 + ... + xn
(2) xs = x + x2 + x3 + ... + xn
(3) s - xs = 1
(4) s(1 - x) = 1
(5) s = 1/(1-x)
QED
Lemma 2: [1/(2n+1)] + ... + [1/(2n + 1 + 2n - 1)] ≥ (1/2)
Proof:
(1) At each n, we have a set of 2n elements.
For example, when n=0, we have 1 element (1/2)
When n=1, we have 2 elements (1/3, 1/4)
When n=2, we have 4 elements (1/5, 1/6, 1/7, 1/8) and so on.
(2) If we pair up two lists of elements in reverse order:
[1/(2n + 1)], [1/(2n+2)], ..., [1/(2n+1+2n-1)]
[1/(2n+1+2n-1)], [1/(2n+1+2n-2), ..., [1/(2n + 1)]
We can see that we have 2n columns where each pair adds up to [1/(2n + 1) + 1/(2n+1) ]
(3) This means that sum of the series of [1/(2n + 1)] thru [1/(2n+1)] is:
(1/2)(2n)[1/(2n + 1) + 1/(2n+1)] =
= 2n-1(2n+1 + 2n + 1)/[(2n+1)(2n + 1)] =
= (2n+1 + 2n + 1)/[(22)(2n + 1)]
(4) Now (1/2) = [(2)(2n + 1)]/[(22)(2n + 1)]
(5) So, this lemma is proven since (2n + 1) ≥ 2 → (2n+1 + 2n + 1) ≥ (2n+1 + 2).
QED
Lemma 3: Harmonic Series Diverges
Let H = 1 + 1/2 + 1/3 + 1/4 + 1/5 + ... + 1/n
Then H has no limit and proceeds toward infinity
Proof:
(1) It is clear that the following sum S diverges and proceeds toward infinity:
S = 1 + 1/2 + 1/2 + 1/2 + ...
(2) Let H1, H2, etc. describe the elements that make up H. (So, that H1 = 1, H2 = 1/2, etc.)
(3) At each each point 2n+1, it is possible to group the elements into:
1/(2n + 1), 1/(2n+2), ..., 1/(2n+1+2n-1)
So that we have:
At [1/(20 + 1)], we have: 1/2
At [1/(21 + 1)], we have: 1/3, 1/4
At [1/(22 + 1)], we have: 1/5, 1/6, 1/7, 1/8
and so on.
(4) Then using Lemma 2 above, we can be sure that the sum of each of these partitions is greater or equal to (1/2)
(5) This gives us that the sum of H ≥ sum of S.
QED
Theorem 4: Euler Product Formula
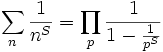
Proof:
(1) 1/(1-x) = 1 + x2 + x3 + ... xn [See Lemma 1 above]
(2) We can see that (1-x)-1 = 1 + x2 + x3 + ... xn
(3) Let x = (1/ps) where p is a prime.
(4) Then we have: (1 - 1/ps)-1 = 1 + 1/ps + 1/p2s + ... + 1/pns
(5) And, ∏(p) [(1 - 1/ps)-1] = ∏(p)[1 + 1/ps + 1/p2s + ... + 1/pns]
where ∏(p) is multiplication of the primes p.
(6) ∏(p)[1 + 1/ps + 1/p2s + ... + 1/pns] =
(1 + 1/2s + 1/22s + ... + 1/2ns)(1 + 1/3s + 1/32s + ... + 1/3ns)(1 + 1/5s + 1/52s + ... + 1/5ns)*...*(1 + 1/ps + 1/p2s + ... + 1/pns) =
= (1*1*1*...*1) + ([1/2s]*1*1*...*1) + (1*[1/3s]*1*...*1) + ([1/22s]*1*1*...*1) + (1*1*[1/5s]*...*1) + ... + ([1/2ns]*[1/3ns]*[1/5ns]*...*[1/pns]) =
= 1 + 1/2s + 1/3s + 1/4s + 1/5s + ... + 1/(2ns*3ns*5ns*...*pns) [By the Fundamental Theorem of Arithmetic]
= ∑(1,∞)ns
QED
Corollary 4.1: There are an infinitude of primes
Proof:
(1) Assume that there are a finite number of primes.
(2) Then there exists an integer p such that p = the maximum prime.
(3) Then, ∏(1,p) [1/(1 - 1/p)] is finite number.
(4) But if s=1, then ∏(1,p) [1/(1 - 1/p)] = ∑(1,∞) 1/n. [See Theorem 4 above]
(5) Now, ∑(1,∞) 1/n is the Harmonic Series which diverges (that is, goes to infinity). [See Lemma 3 above]
(6) Therefore, we have a contradiction and we reject our assumption in step #1.
QED
References
One might ask if Leonhard Euler came up with the zeta function why is it commonly called the Riemann Zeta Function. The answer has to do with the development of the function. While it is true that Euler discovered it, he used it with integer values. Johann Dirichlet would later extend it to real numbers, and Bernhard Riemann extended it to complex numbers. The most interesting properties stem from the complex numbers so it makes sense that it is currently named the Riemann zeta function (see Ed Sandifer's article for details).
So, how did Euler come up with the Euler Product Formula? The Harmonic Series was shown to be divergent (have an infinite sum) by Nicolas Oresme in the 1300s (this is considered one of the high points of mathematics in the middle ages, see Lemma 3 below). Euler wondered if the prime harmonic series (1 + 1/2 + 1/3 + 1/5 + ...) was also divergent. He then began studying the zeta function ζ(s) where:
ζ(s) = 1 + (1/2s) + (1/3s) + ...
For Euler, s is an integer. It turns out that when s=1, ζ(s) = the harmonic series and is therefore divergent. When s ≠ 1, it turns out the the zeta function is convergent, that is, it has a finite limit. In this way, Euler came up with his Product Formula. He then used this result to show that there are an infinitude of primes and the prime harmonic series is infinite. Unfortunately, while his conclusion about the prime harmonic series is correct, his proof today is not considered valid (see Ed Sandier's article for more information). See here for details on the proof for the divergence of the prime harmonic series.
Lemma 1: Infinite Geometric Series
if x ≠ 1, then:
1/(1-x) = 1 + x + x2 + x3 + ... + xn
Proof:
(1) Let s = 1 + x + x2 + x3 + ... + xn
(2) xs = x + x2 + x3 + ... + xn
(3) s - xs = 1
(4) s(1 - x) = 1
(5) s = 1/(1-x)
QED
Lemma 2: [1/(2n+1)] + ... + [1/(2n + 1 + 2n - 1)] ≥ (1/2)
Proof:
(1) At each n, we have a set of 2n elements.
For example, when n=0, we have 1 element (1/2)
When n=1, we have 2 elements (1/3, 1/4)
When n=2, we have 4 elements (1/5, 1/6, 1/7, 1/8) and so on.
(2) If we pair up two lists of elements in reverse order:
[1/(2n + 1)], [1/(2n+2)], ..., [1/(2n+1+2n-1)]
[1/(2n+1+2n-1)], [1/(2n+1+2n-2), ..., [1/(2n + 1)]
We can see that we have 2n columns where each pair adds up to [1/(2n + 1) + 1/(2n+1) ]
(3) This means that sum of the series of [1/(2n + 1)] thru [1/(2n+1)] is:
(1/2)(2n)[1/(2n + 1) + 1/(2n+1)] =
= 2n-1(2n+1 + 2n + 1)/[(2n+1)(2n + 1)] =
= (2n+1 + 2n + 1)/[(22)(2n + 1)]
(4) Now (1/2) = [(2)(2n + 1)]/[(22)(2n + 1)]
(5) So, this lemma is proven since (2n + 1) ≥ 2 → (2n+1 + 2n + 1) ≥ (2n+1 + 2).
QED
Lemma 3: Harmonic Series Diverges
Let H = 1 + 1/2 + 1/3 + 1/4 + 1/5 + ... + 1/n
Then H has no limit and proceeds toward infinity
Proof:
(1) It is clear that the following sum S diverges and proceeds toward infinity:
S = 1 + 1/2 + 1/2 + 1/2 + ...
(2) Let H1, H2, etc. describe the elements that make up H. (So, that H1 = 1, H2 = 1/2, etc.)
(3) At each each point 2n+1, it is possible to group the elements into:
1/(2n + 1), 1/(2n+2), ..., 1/(2n+1+2n-1)
So that we have:
At [1/(20 + 1)], we have: 1/2
At [1/(21 + 1)], we have: 1/3, 1/4
At [1/(22 + 1)], we have: 1/5, 1/6, 1/7, 1/8
and so on.
(4) Then using Lemma 2 above, we can be sure that the sum of each of these partitions is greater or equal to (1/2)
(5) This gives us that the sum of H ≥ sum of S.
QED
Theorem 4: Euler Product Formula
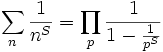
Proof:
(1) 1/(1-x) = 1 + x2 + x3 + ... xn [See Lemma 1 above]
(2) We can see that (1-x)-1 = 1 + x2 + x3 + ... xn
(3) Let x = (1/ps) where p is a prime.
(4) Then we have: (1 - 1/ps)-1 = 1 + 1/ps + 1/p2s + ... + 1/pns
(5) And, ∏(p) [(1 - 1/ps)-1] = ∏(p)[1 + 1/ps + 1/p2s + ... + 1/pns]
where ∏(p) is multiplication of the primes p.
(6) ∏(p)[1 + 1/ps + 1/p2s + ... + 1/pns] =
(1 + 1/2s + 1/22s + ... + 1/2ns)(1 + 1/3s + 1/32s + ... + 1/3ns)(1 + 1/5s + 1/52s + ... + 1/5ns)*...*(1 + 1/ps + 1/p2s + ... + 1/pns) =
= (1*1*1*...*1) + ([1/2s]*1*1*...*1) + (1*[1/3s]*1*...*1) + ([1/22s]*1*1*...*1) + (1*1*[1/5s]*...*1) + ... + ([1/2ns]*[1/3ns]*[1/5ns]*...*[1/pns]) =
= 1 + 1/2s + 1/3s + 1/4s + 1/5s + ... + 1/(2ns*3ns*5ns*...*pns) [By the Fundamental Theorem of Arithmetic]
= ∑(1,∞)ns
QED
Corollary 4.1: There are an infinitude of primes
Proof:
(1) Assume that there are a finite number of primes.
(2) Then there exists an integer p such that p = the maximum prime.
(3) Then, ∏(1,p) [1/(1 - 1/p)] is finite number.
(4) But if s=1, then ∏(1,p) [1/(1 - 1/p)] = ∑(1,∞) 1/n. [See Theorem 4 above]
(5) Now, ∑(1,∞) 1/n is the Harmonic Series which diverges (that is, goes to infinity). [See Lemma 3 above]
(6) Therefore, we have a contradiction and we reject our assumption in step #1.
QED
References
- Ed Sandifer, How Euler Did It?, Mathematical Association of America Online, March, 2006
- Keith Devlin, The Millenium Problems, Basic Books, 2002
- Riemann Hypothesis, Wikipedia
- Riemann Zeta Function, Wikipedia
- Euler Product, Wikipedia
Friday, August 25, 2006
Regular Primes: Next Steps
Ernst Kummer presented his proof that Fermat's Last Theorem is true for regular primes in April of 1847. This is a brilliant proof that introduced the idea of ideal numbers and was the biggest advance in Fermat's Last Theorem up to that point.
Still, there were many questions that were raised: how does one determine the class number for a set of cyclotomic integers that are not characterized by unique factorization? How does one determine when Condition (B) applies for a set of cyclotomic integers. Do irregular primes exist?
Kummer announced that Johann Dirichlet had already found a formula for the class number and would show Dirichlet's work could be applied to the class number for cyclotomic integers. Kummer would later prove that Condition (A) implies Condition (B). Interestingly, out of this, would come a connection between class number and Bernoulli numbers (a prime is regular if it does not divide any of the Bernoulli numbers). Irregular primes do exist and it would later be proved that there are an infinite number of them.
All of this work was done between May and September of 1847. Harold M. Edwards has called this a "an extraordinary tour de force." (Harold M. Edwards, Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory) There turn out to be only 3 irregular primes less than 100, they are: 37, 59, and 67 so Kummer's proof was later used to show that Fermat's Last Theorem is true for integers less than 100. Using techniques from this proof, in 1993, Fermat's Last Theorem was proved to be true for all integers less than 4,000,000. (Of course, all these techniques were superceded when Andrew Wiles presented the first version of his famous proof on June 23, 1993.)
To dive into the advances made with regard to regular primes, it is first necessary to review the Euler Product Formula and show how this formula lead's to Dirichlet's formula for class number. I will show that if a prime does not divide its class number, then this shows that a prime is regular (in other words, using the definition of regular primes, Condition (A) implies Condition (B)) and finally, I will show that 37 is an irregular prime.
Still, there were many questions that were raised: how does one determine the class number for a set of cyclotomic integers that are not characterized by unique factorization? How does one determine when Condition (B) applies for a set of cyclotomic integers. Do irregular primes exist?
Kummer announced that Johann Dirichlet had already found a formula for the class number and would show Dirichlet's work could be applied to the class number for cyclotomic integers. Kummer would later prove that Condition (A) implies Condition (B). Interestingly, out of this, would come a connection between class number and Bernoulli numbers (a prime is regular if it does not divide any of the Bernoulli numbers). Irregular primes do exist and it would later be proved that there are an infinite number of them.
All of this work was done between May and September of 1847. Harold M. Edwards has called this a "an extraordinary tour de force." (Harold M. Edwards, Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory) There turn out to be only 3 irregular primes less than 100, they are: 37, 59, and 67 so Kummer's proof was later used to show that Fermat's Last Theorem is true for integers less than 100. Using techniques from this proof, in 1993, Fermat's Last Theorem was proved to be true for all integers less than 4,000,000. (Of course, all these techniques were superceded when Andrew Wiles presented the first version of his famous proof on June 23, 1993.)
To dive into the advances made with regard to regular primes, it is first necessary to review the Euler Product Formula and show how this formula lead's to Dirichlet's formula for class number. I will show that if a prime does not divide its class number, then this shows that a prime is regular (in other words, using the definition of regular primes, Condition (A) implies Condition (B)) and finally, I will show that 37 is an irregular prime.
Thursday, August 24, 2006
Ideal Numbers: Regular Primes
Today's blog continues the discussion on Ernst Kummer's Theory of Ideal Numbers and his proof of Fermat's Last Theorem for Regular Primes. For historical context, start here.
Today's content is taken straight from Harold M. Edwards Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory.
For standard integers, when we have:
uv = wλ
If gcd(u,v)=1, then we know that u,v are both λth powers. (see Theorem, here)
When it comes to cyclotomic integers, unfortunately, this proof does not hold because to use unique factorization, we have to go through ideal numbers. Today's blog is about the method used by Kummer to apply this reasoning to ideal numbers.
For example, we know that if U is a principal divisor for u and V is a principal divisor for v, and gcd(U,V)=I, then U,V are λth; powers. That is, there exists C,D such that:
U = Cλ, V = Dλ where C,D are ideal numbers.
Lemma 1: gcd(U,V)=I and u(α)v(α)=w(α)n, then there exists C,D such that U=Cn, V=Dn
Proof:
(1) So, we start with gcd(U,V) = I, UV = Wn [We know this since principal divisors have the same relations as their corresponding cyclotomic integers, see here]
(2) Assume that U is not equal to any ideal number Xn
(3) U ≠ I since I is an Xn power [Since In = I]
(4) Now, U is divisible by a prime divisor P. [See Definition 3, here]
(5) So, there exists K such that U = PK
(6) P divides W since Wn = UV = PKV [By applying Euclid's Lemma for Prime Divisors]
(7) So, there exists M such that W=PM
(8) So, Wn = UV = PKV = (PM)n = PnMn
(9) Dividing P from both sides gives us:
KV = P(n-1)Mn
(10) From Euclid's Lemma, P divides K or V.
(11) It can't divide V since it already divides U and gcd(U,V)=I. Therefore, it divides K
(12) We can apply this same argument for each P in P(n-1)
(13) So, we can conclude that P(n-1) divides K.
(14) So, there exists Z such that K = p(n-1)*Z
(15) So, KV = P(n-1)Mn = P(n-1)*Z*V
(16) Dividing p(n-1) from both sides gives us:
ZV = Mn
(17) Now, gcd(Z,V)=1 since Z is a divisor of U and gcd(U,V) = I
(18) Likewise, Z cannot be an n-power. If it were, then U = pnZ would make U an n-power which goes against our assumption in step #2.
(19) Finally, N(Z) is less than N(U) since N(P(n-1)) > 1.
(20) Thus, we have a contradiction by infinite descent.
QED
In order to prove that u,v are both λth powers we need to show that C,D are principal.
This then is the problem that Kummer addressed, under what circumstances can we assume that U = Cλ where U is principal imply that C is also principal.
To help with this question, let's consider an important insight.
Theorem 2: For any ideal number C, if h is the class number, then Ch ~ I
In other words, Ch is principal.
Proof:
(1) Let h be the class number for the cyclotomic integers corresponding to λ
(2) Based on the theorem regarding class numbers (see Theorem, here), we know that all ideal numbers are equivalent to one of the ideal numbers of a representative set: A1, A2, ..., Ah
(3) This means that each of the ideal numbers C, C2, C3, etc. are equivalent to an ideal number Ai
(4) Since there are only h such ideal numbers in the representative set, eventually, there are two ideal numbers Cj and Cj+k that are equivalent to the same Ai and therefore equivalent to each other.
(5) For each ideal number, there exists another ideal number B such that:
CjB is principal [See Lemma 6, here]
(6) Because Cj ~ Cj+k:
Cj+kB is also principal.
(7) But Cj+kB is principal and CjB is principal, then Ck is also principal. (See Lemma 2, here)
(8) Let d be the first power of C that is principal.
So that we have:
Cd ~ I
C, C2, ..., Cd-1 are inequivalent to each other and not principal.
If any of these were equivalent to each other, then there would a power less than d which is principal which goes against our definition of d.
(9) Since I,C, C2, ..., Cd-1 are all inequivalent, then we know that they correspond to d of the Ai which make up the representative set of ideal numbers.
(10) If this exhausts all the elements of the represenative set then d=h so to complete this proof, we only need to consider the situation where d is less than h.
(11) If d is less than h, then there is an ideal number Ai that is not equivalent to any of the powers I,C,C2, ..., Cd-1. Let's call it E.
(12) Then E, EC, EC2, ..., ECd-1 give d more ideal numbers that are inequivalent to each other and inequivalent to the first set of d ideal numbers (in step #11).
(a) Assume ECi ~ ECj where i ≠ j and both i,j are positive integers less than d.
(b) So that we have ECi ~ ECi+k where i+k=j.
(c) Then we have a Ck that is principal where k is less than d which is impossible so we reject our assumption.
(d) Assume E ~ ECi where i is less than d.
(e) Then we have Ci is principal which again is impossible.
(f) Assume ECi ~ Cj
(g) If j ≥ i, then this gives us that E is principal which goes against our assumption step #11 so we can reject this.
(h) If j is less than i, then we have:
ECj+k ~ Cj
This gives us that Cj is principal which goes against our assumption since j is less than d.
(i) So, steps (a) thru (h) prove that this new set E, EC, EC2, ..., ECd-1 is inequivalent to each other and to the powers of Ci.
(13) This either exhausts all Ai of the representative set or we can do the same thing until we are done. At the end, we are left with a disjoint set of d elements each.
(14) This gives us that d divides h so that Cd ~ I → Ch ~ I.
QED
Using the Theorem above, it is now possible to state under what conditions Cλ is principal implies that C is principal.
Corollary 2.1: If Cλ ~ I and λ doesn't divide the class number h, then C ~ I
Proof:
(1) Because λ is prime, if h is not divisible by λ, then there exists m,n such that mh = nλ + 1. [See Lemma 1, here for proof]
(2) I ~ Ch (from Theorem 1 above) so I ~ (Ch)m (see Lemma 1, here)
(3) (Ch)m = Chm = Cnλ+1 = (Cλ)nC
(4) From the given we know that (Cλ) ~ I so we also know that (Cλ)n ~ I.
(5) But I*C = C so (Cλ)nC ~ I*C ~ C
(6) Since I ~ (Cnλ+1) and (Cnλ+1)~C, it follows that C ~ I and therefore, that C is principal.
QED
So, the corollary gives us the justification for considering the situation where λ doesn't divide the class number. This is Kummer's condition (A).
(A) The exponent λ has the property that it does not divide the corresponding class number.
Let's return now to the original problem. Let's say we have:
uv = wλ
where gcd(u,v)=1 and λ does not divide the corresponding class number.
In this case we have that there exists C,D such that Cλ = U, Dλ=V and both C,D are principal.
This gives us that there exists cyclotomic integers c,d such that:
u = ecλ
v = e'dλ
where e,e' are cyclotomic units.
This did not satisfy Kummer. He wanted to find the condition where we could conclude that:
u = cλ
v = dλ
This leads us to condition (B)
(B) The exponent λ should have the property that a unit e in the set of corresponding cyclotomic integers has the following property:
e ≡ integer (mod λ) if and only if there exists a unit e' such that e = (e')λ
To show the value of this. let's consider a second theorem.
Lemma 3: (a0 + a1 + ... + aλ-1)λ ≡ a0λ + a1λ + ... + aλ-1λ (mod λ)
(1) (a + b)λ ≡ aλ + bλ (mod λ) (See Lemma 1, here)
(2) (a + c + d)λ ≡ (a + (c+d))λ ≡ aλ + (c+d)λ (mod λ)
(3) Since (c + d)λ ≡ cλ + dλ (mod λ)
(4) So that we have (a + c + d)λ ≡ aλ + (c+d)λ ≡ aλ + cλ + dλ ≡ (mod λ)
(5) Using the same logic we can show that:
(a + b + c + d + ...)λ = (a + (b + (c + (d + ...)))λ ≡ aλ + bλ + cλ + ... (mod λ)
QED
Corollary 3.1: if g(α) is a cyclotomic integer then g(α)λ ≡ integer (mod λ)
Proof:
(1) Because g(α) is a cyclotomic integer, we have:
g(α) = a0 + a1α + ... + aλ-1αλ-1 [See Lemma 1, here]
(g(α))λ = (a0 + a1α + ... + aλ-1αλ-1)λ ≡ (a0)λ + (a1α)λ + ... + (aλ-1αλ-1)λ (mod λ) [See Lemma 3 above]
(2) Since (αi)λ = (αλ)i = 1i = 1, we have:
(g(α))λ ≡ (a0)λ + (a1)λ + ... + (aλ-1)λ (mod λ) = integer
QED
Theorem 4: if a set of cyclotomic integers corresponding to an odd prime λ satisfies condition (A) and condition (B) and u ≡ integer (mod λ), then if uv=wλ where gcd(u,v)=1, then u,v are λth powers.
Proof:
(1) From Corollary 2.1 above, we have:
u = ecλ
(2) u ≡ ecλ ≡ e*b (mod λ) for some integer b [See Corollary 3.1 above]
(3) So e ≡ integer (mod λ) since e ≡ u/b (mod λ) where b divides u and both b,u are congruent to integers mod (λ).
(4) So therefore (condition B), there exists e' such that e = (e')λ
(5) Let c' = (e'c)
(6) Then we have: u= (c')λ We can make the same argument for v so we are done.
QED
Definition 1: Regular Prime
A prime λ is a regular prime if λ and the corresponding cyclotomic integers satisfy the following two conditions:
(A) The exponent λ has the property that it does not divide the corresponding class number.
(B) The exponent λ should have the property that a unit e in the set of corresponding cyclotomic integers has the following property:
e ≡ integer (mod λ) if and only if there exists a unit e' such that e = (e')λ
We can now use this definion to establish the following theorem:
Lemma 5: For a regular prime λ, if a corresponding cyclotomic integer g(α) has a divisor G which is a λth power and g(α) ≡ integer (mod λ), then there exists a cyclotomic integer h(α) such that g(α) = h(α)λ
Proof:
(1) Since G is λth power, there exists a divisor H such that:
G = Hλ
(2) Since λ is regular (see Definition 1 above), we know that H is principal (see Corollary 1.1 above)
(3) Therefore, there exists h(α) such that H is the principal divisor for h(α) (see Definition 2, here for definition of a principal divisor)
(4) So we have g(α) = eh(α)λ where e is a unit.
(5) Now, g(α) ≡ integer (mod λ) [from the given]
(6) Further, h(α)λ ≡ integer (mod λ) [from Corollary 3.1 above]
(7) So, from this, we have: e ≡ integer/integer ≡ integer (mod λ) [since h(α) divides g(α) and both are congruent to integers mod (λ)
(8) So by Condition (B), there exists e' such that e = (e')λ
(9) Let h'(α) = e'h(α)
(10) Then we have that g(α) = (h'(α))λ
QED
Theorem 6: Criteria for a λth power
if g(α) ≡ nonzero (mod λ), then g(α) = h(α)λ if and only if its divisor is a λth power and g(α) ≡ integer (mod λ)
if g(α) ≡ 0 (mod λ), then g(α) = h(α)λ if and only if its divisor is a λth power and its quotient by the largest power of α - 1 is congruent mod λ to an integer.
Proof:
Case I: g(α) = h(α)λ → ∃ G,H such that G = Hλ and g(α) ≡ integer (mod λ)
(1) Assume g(α) ≡ nonzero (mod λ)
(2) Assume g(α) = h(α)λ
(3) Let G,H be divisors of g(α),h(α)
(4) We can see that G = Hλ so G is a λth power [See Theorem, here]
(5) We can also see that g(α) ≡ integer (mod λ) since h(α)λ ≡ integer (mod λ) from Corollary 3. 1 above.
QED
Case II: G = Hλ and g(α) ≡ integer (mod λ) → ∃ h(α) such that g(α)=h(α)λ
(1) This follows from Lemma 5 above.
QED
Case III: g(α) ≡ 0 (mod λ), g(α) = h(α)λ → an ideal number G is a λth power and quotient by the largest power of α - 1 is congruent mod λ to an integer
(1) Assume g(α) = h(α)λ
(2) Let G,H be the divisor of g(α),h(α)
(3) G = Hλ so we that its divisor G is a λth power. [See Theorem, here]
(4) Since g(α) is divisible by λ, it is divisible by (α-1) since (α-1)λ-1 = λ (see Corollary 3.2, here) so that we have:
g(α) = (α-1)kg'(α) where g'(α) is not divisible by (α - 1) and k ≥ 1.
(5) Since α - 1 is a prime divisor and since g(α) is a λth power, λ must divide k so that we have:
g(α) = [(α-1)k/λ]λg'(α)
(6) By the same argument, the powers of the prime divisors that divide g'(α) must also be divisible by λ so that there exists an ideal number H' such that:
G' = (H')λ
(7) Since G' = (H')λ is principal, then H' must also be principal so that there exists h'(α) such that:
g'(α) = eh'(α)λ where e is a unit.
But since h(α)λ = [(α-1)k/λ]λg'(α), it follows that e must also be a λth power.
(8) But the only way this is possible by Condition B is if e ≡ integer (mod λ)
(9) Therefore, we have g(α) ≡ e * h(α)λ ≡ integer * integer (mod λ)
QED
Case IV: if its divisor G is a λth power and its quotient by the largest power of α - 1 is congruent mod λ to an integer → g(α)=h(α)λ
(1) So there exists an ideal number H such that G = Hλ
(2) g(α) = (α-1)k*g'(α)
(3) So g'(α) ≡ integer (mod λ)
(4) H is principal from Corollary 2.1 above so there exists h(α) such that g(α) = eh(α)λ
(5) Let G' be the principal divisor for g'(α)
(6) Since G is a λth power, all the powers of the prime divisors that make up G must be divisible by λ.
(7) If G' is all the prime divisors minus (α - 1), G' must also be a λth power so that there exists H' such that G' = (H')λ
(6) Since G' = (H')λ is principal, H' is principal (See Corollary 2.1 above)
(7) So there exists h'(α) such that g'(α) ≡ eh'(α)λ
(8) Now g'(α) ≡ integer (mod λ) [from given] and h'(α)λ ≡ integer (mod λ) [from Corollary 3.1 above) so that e ≡ integer (mod λ)
(9) Now using Condition B, this gives us that there exists e' such that e = e'λ
(10) This then gives us that g'(α) = [e'h'(α)]λ
(11) This also gives us that g(α) = [(α-1)k/λe'h'(α)]λ
QED
Kummer made three conjectures regarding regular primes:
(1) There exist irregular primes that do not satisfy conditions (A) and (B). [Proof that 37 is irregular will be proved later]
(2) Condition (A) implies Condition (B). [Proof of this will be presented later]
(3) Regular primes are infinite in number.
This last conjecture is still an open question. There has a been proof that there are infinite irregular primes but no one has proven that there are infinite regular primes. Kummer was able to prove the first two conjectures within a few months after the stated them. The third conjecture he later retracted saying that he didn't know.
Today's content is taken straight from Harold M. Edwards Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory.
For standard integers, when we have:
uv = wλ
If gcd(u,v)=1, then we know that u,v are both λth powers. (see Theorem, here)
When it comes to cyclotomic integers, unfortunately, this proof does not hold because to use unique factorization, we have to go through ideal numbers. Today's blog is about the method used by Kummer to apply this reasoning to ideal numbers.
For example, we know that if U is a principal divisor for u and V is a principal divisor for v, and gcd(U,V)=I, then U,V are λth; powers. That is, there exists C,D such that:
U = Cλ, V = Dλ where C,D are ideal numbers.
Lemma 1: gcd(U,V)=I and u(α)v(α)=w(α)n, then there exists C,D such that U=Cn, V=Dn
Proof:
(1) So, we start with gcd(U,V) = I, UV = Wn [We know this since principal divisors have the same relations as their corresponding cyclotomic integers, see here]
(2) Assume that U is not equal to any ideal number Xn
(3) U ≠ I since I is an Xn power [Since In = I]
(4) Now, U is divisible by a prime divisor P. [See Definition 3, here]
(5) So, there exists K such that U = PK
(6) P divides W since Wn = UV = PKV [By applying Euclid's Lemma for Prime Divisors]
(7) So, there exists M such that W=PM
(8) So, Wn = UV = PKV = (PM)n = PnMn
(9) Dividing P from both sides gives us:
KV = P(n-1)Mn
(10) From Euclid's Lemma, P divides K or V.
(11) It can't divide V since it already divides U and gcd(U,V)=I. Therefore, it divides K
(12) We can apply this same argument for each P in P(n-1)
(13) So, we can conclude that P(n-1) divides K.
(14) So, there exists Z such that K = p(n-1)*Z
(15) So, KV = P(n-1)Mn = P(n-1)*Z*V
(16) Dividing p(n-1) from both sides gives us:
ZV = Mn
(17) Now, gcd(Z,V)=1 since Z is a divisor of U and gcd(U,V) = I
(18) Likewise, Z cannot be an n-power. If it were, then U = pnZ would make U an n-power which goes against our assumption in step #2.
(19) Finally, N(Z) is less than N(U) since N(P(n-1)) > 1.
(20) Thus, we have a contradiction by infinite descent.
QED
In order to prove that u,v are both λth powers we need to show that C,D are principal.
This then is the problem that Kummer addressed, under what circumstances can we assume that U = Cλ where U is principal imply that C is also principal.
To help with this question, let's consider an important insight.
Theorem 2: For any ideal number C, if h is the class number, then Ch ~ I
In other words, Ch is principal.
Proof:
(1) Let h be the class number for the cyclotomic integers corresponding to λ
(2) Based on the theorem regarding class numbers (see Theorem, here), we know that all ideal numbers are equivalent to one of the ideal numbers of a representative set: A1, A2, ..., Ah
(3) This means that each of the ideal numbers C, C2, C3, etc. are equivalent to an ideal number Ai
(4) Since there are only h such ideal numbers in the representative set, eventually, there are two ideal numbers Cj and Cj+k that are equivalent to the same Ai and therefore equivalent to each other.
(5) For each ideal number, there exists another ideal number B such that:
CjB is principal [See Lemma 6, here]
(6) Because Cj ~ Cj+k:
Cj+kB is also principal.
(7) But Cj+kB is principal and CjB is principal, then Ck is also principal. (See Lemma 2, here)
(8) Let d be the first power of C that is principal.
So that we have:
Cd ~ I
C, C2, ..., Cd-1 are inequivalent to each other and not principal.
If any of these were equivalent to each other, then there would a power less than d which is principal which goes against our definition of d.
(9) Since I,C, C2, ..., Cd-1 are all inequivalent, then we know that they correspond to d of the Ai which make up the representative set of ideal numbers.
(10) If this exhausts all the elements of the represenative set then d=h so to complete this proof, we only need to consider the situation where d is less than h.
(11) If d is less than h, then there is an ideal number Ai that is not equivalent to any of the powers I,C,C2, ..., Cd-1. Let's call it E.
(12) Then E, EC, EC2, ..., ECd-1 give d more ideal numbers that are inequivalent to each other and inequivalent to the first set of d ideal numbers (in step #11).
(a) Assume ECi ~ ECj where i ≠ j and both i,j are positive integers less than d.
(b) So that we have ECi ~ ECi+k where i+k=j.
(c) Then we have a Ck that is principal where k is less than d which is impossible so we reject our assumption.
(d) Assume E ~ ECi where i is less than d.
(e) Then we have Ci is principal which again is impossible.
(f) Assume ECi ~ Cj
(g) If j ≥ i, then this gives us that E is principal which goes against our assumption step #11 so we can reject this.
(h) If j is less than i, then we have:
ECj+k ~ Cj
This gives us that Cj is principal which goes against our assumption since j is less than d.
(i) So, steps (a) thru (h) prove that this new set E, EC, EC2, ..., ECd-1 is inequivalent to each other and to the powers of Ci.
(13) This either exhausts all Ai of the representative set or we can do the same thing until we are done. At the end, we are left with a disjoint set of d elements each.
(14) This gives us that d divides h so that Cd ~ I → Ch ~ I.
QED
Using the Theorem above, it is now possible to state under what conditions Cλ is principal implies that C is principal.
Corollary 2.1: If Cλ ~ I and λ doesn't divide the class number h, then C ~ I
Proof:
(1) Because λ is prime, if h is not divisible by λ, then there exists m,n such that mh = nλ + 1. [See Lemma 1, here for proof]
(2) I ~ Ch (from Theorem 1 above) so I ~ (Ch)m (see Lemma 1, here)
(3) (Ch)m = Chm = Cnλ+1 = (Cλ)nC
(4) From the given we know that (Cλ) ~ I so we also know that (Cλ)n ~ I.
(5) But I*C = C so (Cλ)nC ~ I*C ~ C
(6) Since I ~ (Cnλ+1) and (Cnλ+1)~C, it follows that C ~ I and therefore, that C is principal.
QED
So, the corollary gives us the justification for considering the situation where λ doesn't divide the class number. This is Kummer's condition (A).
(A) The exponent λ has the property that it does not divide the corresponding class number.
Let's return now to the original problem. Let's say we have:
uv = wλ
where gcd(u,v)=1 and λ does not divide the corresponding class number.
In this case we have that there exists C,D such that Cλ = U, Dλ=V and both C,D are principal.
This gives us that there exists cyclotomic integers c,d such that:
u = ecλ
v = e'dλ
where e,e' are cyclotomic units.
This did not satisfy Kummer. He wanted to find the condition where we could conclude that:
u = cλ
v = dλ
This leads us to condition (B)
(B) The exponent λ should have the property that a unit e in the set of corresponding cyclotomic integers has the following property:
e ≡ integer (mod λ) if and only if there exists a unit e' such that e = (e')λ
To show the value of this. let's consider a second theorem.
Lemma 3: (a0 + a1 + ... + aλ-1)λ ≡ a0λ + a1λ + ... + aλ-1λ (mod λ)
(1) (a + b)λ ≡ aλ + bλ (mod λ) (See Lemma 1, here)
(2) (a + c + d)λ ≡ (a + (c+d))λ ≡ aλ + (c+d)λ (mod λ)
(3) Since (c + d)λ ≡ cλ + dλ (mod λ)
(4) So that we have (a + c + d)λ ≡ aλ + (c+d)λ ≡ aλ + cλ + dλ ≡ (mod λ)
(5) Using the same logic we can show that:
(a + b + c + d + ...)λ = (a + (b + (c + (d + ...)))λ ≡ aλ + bλ + cλ + ... (mod λ)
QED
Corollary 3.1: if g(α) is a cyclotomic integer then g(α)λ ≡ integer (mod λ)
Proof:
(1) Because g(α) is a cyclotomic integer, we have:
g(α) = a0 + a1α + ... + aλ-1αλ-1 [See Lemma 1, here]
(g(α))λ = (a0 + a1α + ... + aλ-1αλ-1)λ ≡ (a0)λ + (a1α)λ + ... + (aλ-1αλ-1)λ (mod λ) [See Lemma 3 above]
(2) Since (αi)λ = (αλ)i = 1i = 1, we have:
(g(α))λ ≡ (a0)λ + (a1)λ + ... + (aλ-1)λ (mod λ) = integer
QED
Theorem 4: if a set of cyclotomic integers corresponding to an odd prime λ satisfies condition (A) and condition (B) and u ≡ integer (mod λ), then if uv=wλ where gcd(u,v)=1, then u,v are λth powers.
Proof:
(1) From Corollary 2.1 above, we have:
u = ecλ
(2) u ≡ ecλ ≡ e*b (mod λ) for some integer b [See Corollary 3.1 above]
(3) So e ≡ integer (mod λ) since e ≡ u/b (mod λ) where b divides u and both b,u are congruent to integers mod (λ).
(4) So therefore (condition B), there exists e' such that e = (e')λ
(5) Let c' = (e'c)
(6) Then we have: u= (c')λ We can make the same argument for v so we are done.
QED
Definition 1: Regular Prime
A prime λ is a regular prime if λ and the corresponding cyclotomic integers satisfy the following two conditions:
(A) The exponent λ has the property that it does not divide the corresponding class number.
(B) The exponent λ should have the property that a unit e in the set of corresponding cyclotomic integers has the following property:
e ≡ integer (mod λ) if and only if there exists a unit e' such that e = (e')λ
We can now use this definion to establish the following theorem:
Lemma 5: For a regular prime λ, if a corresponding cyclotomic integer g(α) has a divisor G which is a λth power and g(α) ≡ integer (mod λ), then there exists a cyclotomic integer h(α) such that g(α) = h(α)λ
Proof:
(1) Since G is λth power, there exists a divisor H such that:
G = Hλ
(2) Since λ is regular (see Definition 1 above), we know that H is principal (see Corollary 1.1 above)
(3) Therefore, there exists h(α) such that H is the principal divisor for h(α) (see Definition 2, here for definition of a principal divisor)
(4) So we have g(α) = eh(α)λ where e is a unit.
(5) Now, g(α) ≡ integer (mod λ) [from the given]
(6) Further, h(α)λ ≡ integer (mod λ) [from Corollary 3.1 above]
(7) So, from this, we have: e ≡ integer/integer ≡ integer (mod λ) [since h(α) divides g(α) and both are congruent to integers mod (λ)
(8) So by Condition (B), there exists e' such that e = (e')λ
(9) Let h'(α) = e'h(α)
(10) Then we have that g(α) = (h'(α))λ
QED
Theorem 6: Criteria for a λth power
if g(α) ≡ nonzero (mod λ), then g(α) = h(α)λ if and only if its divisor is a λth power and g(α) ≡ integer (mod λ)
if g(α) ≡ 0 (mod λ), then g(α) = h(α)λ if and only if its divisor is a λth power and its quotient by the largest power of α - 1 is congruent mod λ to an integer.
Proof:
Case I: g(α) = h(α)λ → ∃ G,H such that G = Hλ and g(α) ≡ integer (mod λ)
(1) Assume g(α) ≡ nonzero (mod λ)
(2) Assume g(α) = h(α)λ
(3) Let G,H be divisors of g(α),h(α)
(4) We can see that G = Hλ so G is a λth power [See Theorem, here]
(5) We can also see that g(α) ≡ integer (mod λ) since h(α)λ ≡ integer (mod λ) from Corollary 3. 1 above.
QED
Case II: G = Hλ and g(α) ≡ integer (mod λ) → ∃ h(α) such that g(α)=h(α)λ
(1) This follows from Lemma 5 above.
QED
Case III: g(α) ≡ 0 (mod λ), g(α) = h(α)λ → an ideal number G is a λth power and quotient by the largest power of α - 1 is congruent mod λ to an integer
(1) Assume g(α) = h(α)λ
(2) Let G,H be the divisor of g(α),h(α)
(3) G = Hλ so we that its divisor G is a λth power. [See Theorem, here]
(4) Since g(α) is divisible by λ, it is divisible by (α-1) since (α-1)λ-1 = λ (see Corollary 3.2, here) so that we have:
g(α) = (α-1)kg'(α) where g'(α) is not divisible by (α - 1) and k ≥ 1.
(5) Since α - 1 is a prime divisor and since g(α) is a λth power, λ must divide k so that we have:
g(α) = [(α-1)k/λ]λg'(α)
(6) By the same argument, the powers of the prime divisors that divide g'(α) must also be divisible by λ so that there exists an ideal number H' such that:
G' = (H')λ
(7) Since G' = (H')λ is principal, then H' must also be principal so that there exists h'(α) such that:
g'(α) = eh'(α)λ where e is a unit.
But since h(α)λ = [(α-1)k/λ]λg'(α), it follows that e must also be a λth power.
(8) But the only way this is possible by Condition B is if e ≡ integer (mod λ)
(9) Therefore, we have g(α) ≡ e * h(α)λ ≡ integer * integer (mod λ)
QED
Case IV: if its divisor G is a λth power and its quotient by the largest power of α - 1 is congruent mod λ to an integer → g(α)=h(α)λ
(1) So there exists an ideal number H such that G = Hλ
(2) g(α) = (α-1)k*g'(α)
(3) So g'(α) ≡ integer (mod λ)
(4) H is principal from Corollary 2.1 above so there exists h(α) such that g(α) = eh(α)λ
(5) Let G' be the principal divisor for g'(α)
(6) Since G is a λth power, all the powers of the prime divisors that make up G must be divisible by λ.
(7) If G' is all the prime divisors minus (α - 1), G' must also be a λth power so that there exists H' such that G' = (H')λ
(6) Since G' = (H')λ is principal, H' is principal (See Corollary 2.1 above)
(7) So there exists h'(α) such that g'(α) ≡ eh'(α)λ
(8) Now g'(α) ≡ integer (mod λ) [from given] and h'(α)λ ≡ integer (mod λ) [from Corollary 3.1 above) so that e ≡ integer (mod λ)
(9) Now using Condition B, this gives us that there exists e' such that e = e'λ
(10) This then gives us that g'(α) = [e'h'(α)]λ
(11) This also gives us that g(α) = [(α-1)k/λe'h'(α)]λ
QED
Kummer made three conjectures regarding regular primes:
(1) There exist irregular primes that do not satisfy conditions (A) and (B). [Proof that 37 is irregular will be proved later]
(2) Condition (A) implies Condition (B). [Proof of this will be presented later]
(3) Regular primes are infinite in number.
This last conjecture is still an open question. There has a been proof that there are infinite irregular primes but no one has proven that there are infinite regular primes. Kummer was able to prove the first two conjectures within a few months after the stated them. The third conjecture he later retracted saying that he didn't know.
Subscribe to:
Posts (Atom)
