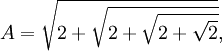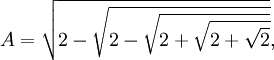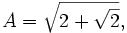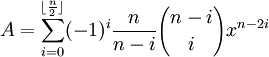Van Roomen's Problem: Solution Explained

In today's blog, I will provide the solution to Van Roomen's problem. Van Roomen's problem established François Viète as one of the most important mathematicians of his day, showed the relevance of trigonometry to solving algebraic equations, and finally paved the way to Albert Girard's insight (and Carl Friedrich Gauss's brilliant proof) of the Fundamental Theorem of Algebra.

First, here is the problem posed by Adriaan Van Roomen (see here for more details):

Solve for x where:

(45)x - (3,795)x³ + (95,634)x⁵ - (1,138,500)x⁷ + (7,811,375)x⁹ - (34,512,075)x¹¹ + (105,306,075)x¹³ - (232,676,280)x¹⁵ + (384,942,375)x¹⁷ - (488,494,125)x¹⁹ + (483,841,800)x²¹ - (378,658,800)x²³ + (236,030,652)x²⁵ - (117,679,100)x²⁷ + (46,955,700)x²⁹ - (14,945,040)x³¹ + (3,764,565)x³³ - (740,259)x³⁵ + (111,150)x³⁷ - (12,300)x³⁹ + (945)x⁴¹ - (45)x⁴³ + x⁴⁵ = A

and:



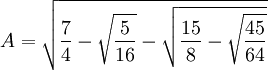
Let's start by simplifying Van Roomen's equation.

If we define:

F_n(x) =



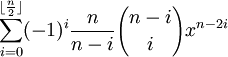
Then, it turns out (see here for the details) that:

F₄₅(x) =

(45)x - (3,795)x³ + (95,634)x⁵ - (1,138,500)x⁷ + (7,811,375)x⁹ - (34,512,075)x¹¹ + (105,306,075)x¹³ - (232,676,280)x¹⁵ + (384,942,375)x¹⁷ - (488,494,125)x¹⁹ + (483,841,800)x²¹ - (378,658,800)x²³ + (236,030,652)x²⁵ - (117,679,100)x²⁷ + (46,955,700)x²⁹ - (14,945,040)x³¹ + (3,764,565)x³³ - (740,259)x³⁵ + (111,150)x³⁷ - (12,300)x³⁹ + (945)x⁴¹ - (45)x⁴³ + x⁴⁵

The complex value for A can also be simplified. It turns out that (see Lemma 7, here):



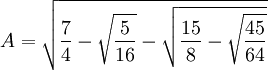
= 2 sin(π/[15])

Now, analyzing the above equation for F_n, also establishes the following linkage to trigonometry (see Corollary 1.2, here for details):

For any odd integer n ≥ 1:

2 sin(nα) = (-1)^(n-1)/2*F_n(2sinα)

So, for n = 45, we have:

2sin(45α) = (-1)²²F₄₅(2sinα) = F₄₅(2sinα)

Now, we have enough to derive the solution that Van Roomen was interested in since:

2sin(45α) = F₄₅(2sinα) = 2 sin(π/[15])

We just need to solve for α so that:

45α = π/15 so α = π/[15*45].

Thus, the solution is x = 2sinα = 2sin(π/[15*45])

Indeed, if we look at all of Van Roomen's examples that he gave (see here for details), the same solution applies (see here for the proofs). In each case, you will find that if A = 2 sin(θ), then x = 2sin(θ/45).

This solution was enough for Van Roomen but this was not enough for Viète. He went on to show that there are 45 different solutions for x (44 in addition to the one listed above) with 23 positive solutions and 22 negative solutions. This insight would be very important to establishing the Fundamental Theorem of Algebra.

How did he do it?

Well, we know that for sin, sin(θ) = sin(θ + 2π). [See Property 5, here for details if needed]

This means that if we define α_k = α + n*(2π/45), then in all cases:

2sin(45*[α + n*(2π/45)]) = 2sin(π/15).

We know that there are 45 solutions because (n*2π/45) for n =0, ..., 44 are all distinct values. At n=45, 45*2π/45 = 2π which is the same value as n=0 since sine is a repeating function and so on for any value n ≥ 45.

We know that for n= 0, ..., 22, sin(α + n*(2π/45)) ≥ 0 and for n = 23, ..., 44 sin(α + n*(2π/45)) is negative.

In my next blog, I will show how François Viète came up with his own solution to the cubic equation.

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Solving Van Roomen's Problem: Step Five

In today's blog, I show how we can use the trigonometric identities in my previous blog to simplify Van Roomen's x and A examples. To see the statement of Van Roomen's problem, start here.

The content in today's blog is taken from Jean-Pierre Tignol's Galois' Theory of Algebraic Equations.

Lemma 1:



= 2 sin(15π/2⁵)

Proof:

(1) cos(90°) = 0 [See Property 7, here]

(2) cos(2π/4) = cos(π/2) = cos(90°) = 0 [See here for review of radians]

(3) 2cos(π/4) = ±√2 + 2cos(π/2) [See Lemma 1, here]

(4) So, 2cos(π/4) = ±√2

(5) 2cos(π/8) = ±√2 + 2cos(π/4) = ±√2 + √2

(6) 2cos(π/16) = ±√2 + 2cos(π/8) = ±√2 + √(2 + √2)

(7) 2cos(π/32) = ±√2 + 2cos(π/16) = ±√2 + √[2 + √(2 + √2)]

(8) 2cos(π/32) = 2sin(π/2 - π/32) [See Lemma 1, here]

(9) 2sin(π/2 - π/32) = 2sin(16π/32 - π/32) = 2sin(15π/32) = 2sin(15π/2⁵)

QED

Lemma 2:



= 2 sin(π/[2⁵*3])

Proof:

(1) 2cos(π/6) = √3 [See Corollary 1.1, here]

(2) 2cos(π/12) = ±√2 + 2cos(π/6) [See Lemma 1, here]

(3) 2cos(π/12) = ±√2 + √3

(4) 2cos(π/24) = ±√2 + 2cos(π/12) = ±√2 + √(2 + √3)

(5) 2cos(π/48) = ±√2 + 2cos(π/24) = ±√2 + √[2 + √(2 + √3)]

(5) 2sin(π/96) = ±√2 - 2cos(π/48) [See Lemma 2, here]

(6) 2sin(π/96) = 2sin(π/[2⁵*3]) = ±√2 - √{2 + √[2 + √(2 + √3)]}

QED

Lemma 3:



= 2 sin(15π/2⁶)

Proof:

(1) From step#6 in Lemma 1 above, we have:

2cos(π/16) = ±√2 + √(2 + √2)

(2) Using Lemma 2 here, we have:

2sin(π/32) = ±√2 - 2cos(π/16) = ±√2 - √[2 + √(2 + √2)]

(3) 2cos(π/2 - π/32) = 2sin(π/32) [See Corollary 1.1, here]

(4) 2cos(π/2 - π/32) = 2cos(16π/32 - π/32) = 2cos(15π/32)

(5) 2sin(15π/64) = ±√2 - 2cos(π/16) = ±√2 - √{2 - √[2 + √(2 + √2)]}

(6) 2sin(15π/64) = 2sin(15π/[2⁶])

QED

Lemma 4:



= 2sin(π/[2⁶*3])

Proof:

(1) Using step #5 from Lemma 2 above, we have:

2cos(π/2⁴*3) = ±√2 + 2cos(π/24) = ±√2 + √[2 + √(2 + √3)]

(2) So we have:

2cos(π/2⁵*3) = ±√2 + 2cos(π/2⁴*3) = ±√2 + √{2 + √[2 + √(2 + √3)]}

(3) And also:

2sin(π/2⁶*3) = ±√2 - 2cos(π/2⁵*3) =

= ±√2 - √(2 + √{2 + √[2 + √(2 + √3)]})

QED

Lemma 5:



= 2sin(3π/2³)

Proof:

(1) From Lemma 1 above, step #5, we have:

2cos(π/8) = ±√2 + 2cos(π/4) = ±√2 + √2

(3) Using Lemma 1 here we have:

2cos(π/8) = 2sin(π/2 - π/8) = 2sin(4π/8 - π/8) = 2sin(3π/8) = 2sin(3π/2³)

QED

Lemma 6:



= 2sin(π/[2³*3*5])

Proof:

(1) π/5 - π/6 = 6π/30 - 5π/30 = π/30

(2) 2cos(π/30) = 2cos(π/5 - π/6) = 2cos(π/5)cos(π/6) + 2sin(π/5)sin(π/6) [See Theorem 2, here for cosine addition/subtraction rule]

(3) Using previous results, we can compute cos(π/10) and sin(π/10):

cos(π/10) = sin(π/2 - π/10) = sin(5π/10 - π/10) = sin(4π10) = sin(2π/5) [See here Lemma 1,here]

sin(2π/5) = (1/2)√(5 + √5)/2 [See Lemma 6, here]

sin(π/10) = cos(π/2 - π/10) = cos(2π/10) [See Corollary 1.1, here]

cos(2π/5) = (√5 - 1)/4 [See Lemma 5, here]

(4) Now, we can use cos(π/10), sin(π/10) to compute cos(π/5) and sin(π/5):

Using the cosine double angle formula (see Corollary 3.1, here):
cos(2x) = 2cos²(x) - 1

So,
cos(2*π/10) = cos(π/5) = 2cos²(π/10) - 1 = (2)(1/8)[5 + √5] - 1 = 5/4 + (√5)/4 - 4/4 = (√5 + 1)/4

Now, we can use sin²(π/5) + cos²(π/5) = 1 [see Corollary 2, here], to get:

sin(π/5)² = 1 - cos²(π/5) = 16/16 - (1/16)(5 + 2√5 + 1) = (1/16)[10 - 2√5 ]

This gives us:
sin(π/5) = (1/4)√10 - 2√5

(5) Using a previous result (see Corollary 1.2, here), we know that:

cos(π/6) = cos(30°) = √3/2

sin(π/6) = sin(30 °) = (1/2)

(6) So, this gives us that:

cos(π/30) = 2[(√5 + 1)/4][√3/2] + 2[(1/4)√10 - 2√5][(1/2)] =

= (1/4)[√15 + √3] + (1/4)[√10 - 2√5] =√(3/16) + √(15/16) + √(5/8) - √(5/64).

(7) 2cos(π/[2²*5*3]) = ±√2 + 2cos(π/30) [See Lemma 1, here]

So that:
2cos(π/[2²*5*3]) = ±√{2 + √(3/16) + √(15/16) + √[(5/8) - √(5/64)]}

(8) 2sin(π/[2³*5*3]) = ±√2 - 2cos(π/[2²*5*3]) [See Lemma 2, here]

So:
2sin(π/[2³*5*3]) = ±√2 - √{2 + √(3/16) + √(15/16) + √[(5/8) - √(5/64)]}

QED

Lemma 7:



= 2 sin(π/[3*5])

Proof:

(1) 2sin(π/15) = (1/2)√7 - √5 - √(30 - 6√5) [See Corollary 7.1, here]

(2) Since (1/2) = (1/√4), we have:

2sin(π/15) = √(7/4) - √(5/16) - √[(30 - √[36*5])/16] =

= √(7/4) - √(5/16) - √[15/8 - √(36*5/16*16)] =

= √(7/4) - √(5/16) - √[15/8 - √(9*5/4*16)] =

= √(7/4) - √(5/16) - √[15/8 - √(45/64)]

QED

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Solving Van Roomen's Problem: Step Four

In today's blog, I will present some simple trigonometric identities that can be used to simplify Van Roomen's examples of x and A values. For those who want an introduction to Van Roomen's Problem, start here. In my next blog, I will apply these lemmas to Van Roomen's problem.

The content in today's blog is taken from Jean-Pierre Tignol's Galois' Theory of Algebraic Equations.

Let me start by introducting the some basic ideas from trigonometry.

Lemma 1: 2 cos(α/2) = ± √2 + 2 cos α

Proof:

(1) cos(2x) = 2 cos²(x) - 1 [See Corollary 3.1, here]

(2) Let x = α/2, then we get:

cos(α) = 2cos²(α/2) - 1

(3) Rearranging terms gives us:

2cos²(α/2) = cos(α) + 1

(4) Multiplying both sides by 2 gives us:

4cos²(α/2) = 2cos(α) + 2

(5) Finally, taking the square root of both sides gives us:

2cos(α/2) = ±√2 + 2cos(α)

QED

Lemma 2: 2 sin(α/2) = ± √2 - 2 cos α

Proof:

(1) cos(2x) = 1 - 2 sin²(x) [See Corollary 3.1, here]

(2) Let x = α/2, then we get:

cos(α) = 1 - 2sin²(α/2)

(3) Rearranging terms gives us:

2sin²(α/2) = 1 - cos(α)

(4) Multiplying both sides by 2 gives us:

4sin²(α/2) = 2 - 2cos(α)

(5) Finally, taking the square root of both sides gives us:

2sin(α/2) = ±√2 - 2cos(α)

QED

Lemma 3: 2 cos(π/3) = 1

Proof:

(1) 2cos(π/3) = 2cos(60°) [See here for review of radians]

(2) 2cos(60°) = 2(1/2) = 1 [See Corollary 1.2, here]

QED

Lemma 4: 2 sin(π/3) = √3

Proof:

(1) 2sin(π/3) = 2sin(60°) [See here for review of radians]

(2) 2sin(60°) = 2*(√3/2) = √3 [See Corollary 1.2, here]

QED

Lemma 5: 2cos(2π/5) = (√5 - 1)/2

Proof:

(1) cos (2π/5) = (√5 - 1)/4 [See Corollary 1.1, here]

(2) So:

2cos(2π/5) = (√5 - 1)/2

QED

Lemma 6: 2sin(2π/5) = √(5 + √5)/2

Proof:

(1) sin (2π/5) = √5 + √5/8 [See Corollary 1.1, here]

(2) So:

2*sin (2π/5) = 2(1/2)√5 + √5/2 = √(5 + √5)/2

QED

Lemma 7: 2cos(π/15) = (1/4)(√30 + 6√5 + √5 - 1)

Proof:

(1) 2π/5 - π/3 = 6π/15 - 5π/15 = π/15

(2) 2cos(π/15) = 2cos(2π/5 - π/3) = 2cos(2π/5)cos(π/3) + 2sin(2π/5)sin(π/3) [See Theorem 2, here]

2cos(2π/5) = (√5 - 1)/2 [See Lemma 5 above]

cos(π/3) = 1/2 [See Lemma 3 above]

2sin(2π/5) = √(5 + √5)/2 [See Lemma 6 above]

sin(π/3) = √3/2 [See Lemma 4 above]

(4) 2cos(π/15) = [ (√5 - 1)/2 ][1/2] + [√(5 + √5)/2][√3/2] =

= [ (√5 - 1)/4] +(1/2) [√(15 + 3√5)/2] = [ (√5 - 1)/4] + (1/4)[√(30 + 6√5)]

= (1/4)[ √5 - 1 + √(30 + 6√5)]

QED

Corollary 7.1: 2sin(π/15) = (1/2)√7 - √5 - √(30 - 6√5)

Proof:

(1) 2cos(π/15) = (1/4)(√30 + 6√5 + √5 - 1) [See Lemma 7 above]

(2) 4cos²(π/15) = (1/16)(30 + 6√5 + 5 + 1 + 2(√30 + 6√5)(√5) - 2√30 + 6√5 - 2√5 = (1/16)(36 + 4√5 + 2(√30 + 6√5)(√5) - 2√30 + 6√5)

(3) Since sin²(x) + cos²(x) = 1 [See Corollary 2, here], we have:

4sin²(π/15) = 4 - cos²(π/15) =

= (1/16)[64 - 36 - 4√5 - 2(√30 + 6√5)(√5) + 2√30 + 6√5 ] =

= (1/16)[28 - 4√5 - 2(√30 + 6√5)(√5) + 2√30 + 6√5] =

= (1/16)[28 - 4√5 - (√30 + 6√5)(2√5 - 2)] =

= (1/16)[28 - 4√5 - (√30 + 6√5)(√2√5 - 2)²] =

= (1/16)[28 - 4√5 - (√30 + 6√5)(√20 - 8√5 + 4)] =

= (1/16)[28 - 4√5 - (√30 + 6√5)(√24 - 8√5)] =

= (1/16)[28 - 4√5 - (√720 - 240√5 + 144√5 - 240)] =

= (1/16)[28 - 4√5 - (√480 - 96√5] =

= (1/16)[28 - 4√5 - 4(√30 - 6√5]


(4) 2sin(π/15) = √(1/16)[28 - 4√5 - 4(√30 -6√5] =

= (1/4)√[28 - 4√5 - 4(√30 -6√5] =

= (1/2)√[7 - √5 - √30 -6√5] =

QED

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Solving Van Roomen's Problem: So far

So, up to know, I've shown that Van Roomen's monster equation: (see here):

(45)x - (3,795)x³ + (95,634)x⁵ - (1,138,500)x⁷ + (7,811,375)x⁹ - (34,512,075)x¹¹ + (105,306,075)x¹³ - (232,676,280)x¹⁵ + (384,942,375)x¹⁷ - (488,494,125)x¹⁹ + (483,841,800)x²¹ - (378,658,800)x²³ + (236,030,652)x²⁵ - (117,679,100)x²⁷ + (46,955,700)x²⁹ - (14,945,040)x³¹ + (3,764,565)x³³ - (740,259)x³⁵ + (111,150)x³⁷ - (12,300)x³⁹ + (945)x⁴¹ - (45)x⁴³ + x⁴⁵ = A

simplifies to this one when n = 45 (see here for proof):



If we generalize the above equation to F_n (see below), there is an interesting recurrence relation that emerges (see here for details).

If we define:

F_n(x) =



Then:

F_n(x) = x*F_n-1(x) - F_n-2(x).

Finally, we can introduce trigonometry to the equation defined above (see here for proof) to get:

for any integer n ≥ 1:

2cos(nα) = F_n(2cosα)

For any odd integer n ≥ 1:

2 sin(nα) = (-1)^(n-1)/2*F_n(2sinα)


Now, let's see if we can simplify the examples that Van Roomen gives for x and A (see here for details). It turns out that all can be simplified using trigonometric identities.

Here are three examples that Van Roomen provides. I should note that in Van Roomen's original problem, he made a mistake on example 2. For purposes of this blog, I have corrected his mistake. (See Jean-Pierre Tignol's book for more details).

Example 1:

If



Then:



Example 2:

If:



Then:



Example 3:

If:



Then:




In my next blog, I will show how each of these values can be simplified using trigonometry.

References

• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Solving Van Roomen's Problem: Step Three

The third step in solving Van Roomen's problem is realizing its relation to trigonometry. Using F_n(x) defined in my last blog (see here), I will show that:

2cos(nα) = F_n(2cosα) where n ≥ 1.

and

2sin(nα) = (-1)^(n-1)/2F_n(2sinα) where n is odd and n ≥ 1.

Here are the details:

Lemma 1: n ≥ 1 → 2 cos(n)α = (2cos α)(2 cos (n-1)α) - 2 cos(n-1)α

Proof:

(1) From the addition and subtraction cosine formulas [see Theorem 1, here], we know that:

cos (a + b) = cos a cos b + sin a sin b

cos (a - b) = cos a cos b - sin a sin b

(2) Adding these two identities together gives us:

cos (a + b) + cos (a - b) = cos a cos b + cos a cos b = 2cos a cos b

Or in other words:

cos (a + b) = 2 cos a cos b - cos (a - b)

(3) Since a,b can be any value, let b = α, let a = (n-1)α

So that:

a + b = (n-1)b + b = (n-1+1)b = nα

a - b = (n-1)b - b = (n-2)α

(4) This then gives us that:

cos (nα) = (cos α)(2 cos(n-1)α) - cos(n-2)α

Or equivalently:

2 cos (nα) = (2 cos α)(2 cos(n-1)α) - 2 cos(n-2)α

QED

This trigonometric identity is relevant to Van Roomen's problem because it fits the same structure as F_n

In my previous blog, I showed that F_n(x) = x*F_n-1(x) - F_n-2(x).

Now, if x = 2 cos α, then we have:

F_n(2 cos α) = (2 cos α)*F_n-1(2 cos α) - F_n-2(2 cos α)

This brings us to the corollary:

Corollary 1.1: 2 cos(nα) = F_n(2 cos α)

Proof:

(1) At n = 1:

F₁ = x = 2 cos α = 2 cos(n α)

(2) At n = 2:

F₂ = x² - 2 = (2 cos α)² - 2 = 2(2 cos²(α) - 1)

Since sin²(x) + cos²(x) = 1 (see Corollary 2, here), we have :

2(2 cos²(α) - 1) = 2(2 cos²(α) - [sin²(α) + cos²(α)] ) = 2[cos²(α) - sin²(α)]

Using the formula for cos(2x) (see Lemma 3, here), we get:

2[cos²(α) - sin²(α)] = 2 (cos 2 α)

(3) So, let's assume that F_n(2 cos α) = 2 cos n α up to n-1 where n ≥ 3.

(4) Now, using our previous formula (see Theorem 1, here), we know that:

F_n(x) = x*F_n-1(x) - F_n-2(x)

(5) Using our assumption in step #3, we have:

F_n(2 cos α) = (2 cos α)*(2 cos(n-1)α) - (2 cos(n-2)α)

(6) Now, using Lemma 1 above, we know that:

2 cos nα = (2 cos α)*(2 cos (n-1)α) - (2 cos(n-2)α) so that by induction (see Theorem, here for review if needed), we have proven that:

F_n(2 cos α) = 2 cos n α

QED

But we are not yet done, we can also show:

Corollary 1.2: For all odd n ≥ 1:

2 sin nα = (-1)^(n-1)/2F_n(2 sin α)

Proof:

(1) From a previous result (see Lemma 1, here), we know that:

cos(z) = sin(z + π/2) where z is any number in radians (see here for review of radians).

(2) Let z = x - π/2

(3) Then:

cos(x - π/2) = sin(x - π/2 + π2) = sin(x)

(4) Now from Corollary 1.1 above, we have:

2 cos(nα) = F_n(2 cos α)

(5) Since α can be any value let α = β - π/2

so that:

2 cos(n[β - π/2]) = 2 cos(nβ - nπ/2) = 2 cos([nβ - (n-1)π/2] - π/2) = 2 sin(nβ - (n-1)π/2)

and

F_n(2 cos (β - π/2)) = F_n(2sin(β))

(6) Using the formula for sin(a+b) [see Theorem 1, here], we get:

sin(nβ - (n-1)π/2) = sin(nβ)cos([n-1]π/2) - cos(nβ)sin([n-1]π/2)

(7) Since n is odd, we know that n-1 is even and there exists m such that (n-1)=2m which gives us:

cos([n-1]π/2) = cos(mπ) = (-1)^m since:

(a) n ≥ 1 so m ≥ 0.

(b) cos(0) = 1, cos(π)= -1 [See Property 6, here]

(c) Finally cos(x + 2π) = x [See Property 5, here]

(d) If m is even, then mπ is divisible by 2π and cos(mπ) = 1 = (-1)^m

(e) If m is odd, then mπ is not divisible by 2π and cos(mπ) = -1 = (-1)^m

Likewise:

sin([n-1]π/2) = sin(mπ) = 0 since:

(a) n ≥ 1 so m ≥ 0.

(b) sin(0) = 0, sin(π) = 0 [see Property 1, here]

(c) sin(x + 2π) = sin x [See Property 5, here]

(d) Putting this together, we can see that mπ ≡ 0 or ≡ π (mod 2π) and either way sin(mπ)=0.

(8) So that we have:

2 sin(nβ - (n-1)π/2) = 2*[sin(nβ)cos([n-1]π/2) - cos(nβ)sin([n-1]π/2)] = 2*(-1)^(n-1)/2*sin(nβ) - cos(nβ)*0 = 2*(-1)^(n-1)/2sin(nβ)

(9) Using step #8 and combining it with step #4 and step #5 gives:

2*(-1)^(n-1)/2sin(nβ) = F_n(2sin(β))

(10) Multiplying both sides by (-1)^(n-1)/2 gives us:

2sin(nβ) = (-1)^(n-1)/2F_n(2sin(β))

QED

References

• "Cos of multiples of x, in terms of cos x ", MathHelp
• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001

Solving Van Roomen's Problem: Step Two

In my previous blog, I showed how Van Roomen's problem could be reduced to a summation formula:

(45)x - (3,795)x³ + (95,634)x⁵ - (1,138,500)x⁷ + (7,811,375)x⁹ - (34,512,075)x¹¹ + (105,306,075)x¹³ - (232,676,280)x¹⁵ + (384,942,375)x¹⁷ - (488,494,125)x¹⁹ + (483,841,800)x²¹ - (378,658,800)x²³ + (236,030,652)x²⁵ - (117,679,100)x²⁷ + (46,955,700)x²⁹ - (14,945,040)x³¹ + (3,764,565)x³³ - (740,259)x³⁵ + (111,150)x³⁷ - (12,300)x³⁹ + (945)x⁴¹ - (45)x⁴³ + x⁴⁵ =



where n = 45.

In today's blog, I will show how a recurrence relation can be introduced to simplify the problem further.

The key insight comes to generalizing the above summation formula. For example, let's define:

F_n(x) =



It turns out that it is possible to show that for any n ≥ 1:

2cos(nα) = F_n(2cosα)

For any odd n ≥ 1:

2 sin(nα) = (-1)^(n-1)/2*F_n(2sinα)

François Viète knew both of these identities and he would use them to find his solutions to Van Roomen's problem. In today's blog, I will show the proof for the recurrent relation and in my next blog, I will show how this recurrence relation leads to the trigonometric identities above.

Theorem 1: Recurrence Formula

If:

F_n(x) =



Then:

F_n(x) = x*F_n-1(x) + F_n-2(x)

Proof:

(1) F₁(x) = (-1)⁰*(1/1)*[(1!)/(0!1!)]x^1-0 = x

(2) F₂(x) = (-1)⁰*(2/2)*[(2!)/(0!2!)]x^2-0 + (-1)¹*(2/1)*[(1!)/(1!0!)]x^2-2 = x² - 2

(3) F₃(x) = (-1)⁰*(3/3)*[(3!)/(0!3!)]x^3-0 + (-1)¹*(3/2)*[(2!)/(1!1!)]x^3-2 = x³ - 3x

(4) We can see that x*F₂(x) - F₁(x) = x*(x² - 2) - x = x³ - 3x.

(5) So, we can assume that the recurrence formula is true up to some integer n-1 where n ≥ 4, that is:

F_n-1(x) = x*F_n-2(x) - F_n-3(x)

(6) Now, x*F_n-1(x) =



=


(7) Likewise, F_n-2(x) =



=



=



(8) So, we see that: x*F_n-1(x) - F_n-2(x) =





where if n is odd,

C = 0

and if n is even,

C =

-(-1)^{(n/2 - 1)}[(n-2)/(n-1-n/2)][(n-1-n/2)!/(n/2-1)!(n-1-n/2-(n/2-1))!]x^n-2(n/2) =

= (-1)^(n/2)[(n-2)/(n/2-1)][(n/2-1)!/(n/2 -1)!(0!)]x⁰ =

= (-1)^(n/2)[(n-2)]/[(n/2-1)](1)(1) = (-1)^(n/2)(n-2)*(2)/(n-2) =

= (-1)^(n/2)*2

(9) So, x*F_n-1(x) - F_n-2(x) - C - x_n =



(10) Focusing solely on the middle part, we see that:
















(11) If n is odd:

F_n(x) =



(12) If n is even:

F_n(x) =



(13) So, either way we have:

F_n(x) = x*F_n-1(x) - F_n-2(x).

QED