(45)x - (3,795)x3 + (95,634)x5 - (1,138,500)x7 + (7,811,375)x9 - (34,512,075)x11 + (105,306,075)x13 - (232,676,280)x15 + (384,942,375)x17 - (488,494,125)x19 + (483,841,800)x21 - (378,658,800)x23 + (236,030,652)x25 - (117,679,100)x27 + (46,955,700)x29 - (14,945,040)x31 + (3,764,565)x33 - (740,259)x35 + (111,150)x37 - (12,300)x39 + (945)x41 - (45)x43 + x45 = A
simplifies to this one when n = 45 (see here for proof):
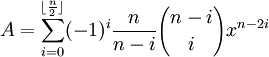
If we generalize the above equation to Fn (see below), there is an interesting recurrence relation that emerges (see here for details).
If we define:
Fn(x) =
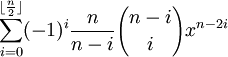
Then:
Fn(x) = x*Fn-1(x) - Fn-2(x).
Finally, we can introduce trigonometry to the equation defined above (see here for proof) to get:
for any integer n ≥ 1:
2cos(nα) = Fn(2cosα)
For any odd integer n ≥ 1:
2 sin(nα) = (-1)(n-1)/2*Fn(2sinα)
Now, let's see if we can simplify the examples that Van Roomen gives for x and A (see here for details). It turns out that all can be simplified using trigonometric identities.
Here are three examples that Van Roomen provides. I should note that in Van Roomen's original problem, he made a mistake on example 2. For purposes of this blog, I have corrected his mistake. (See Jean-Pierre Tignol's book for more details).
Example 1:
If
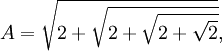
Then:

Example 2:
If:
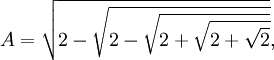
Then:

Example 3:
If:
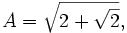
Then:

In my next blog, I will show how each of these values can be simplified using trigonometry.
References
- Jean-Pierre Tignol, Galois' Theory of Algebraic Equations
, World Scientific, 2001

No comments:
Post a Comment