Van Roomen's Problem

Adriaan Van Roomen was a professor of mathematics and medicine in Louvain who had developed a strong reputation as one of the top mathematicians of his age. In 1593, he published a survey of the most important living mathematicians. In this work, he proposed a math problem that he dared any of these top mathematicians to solve:

(45)x - (3,795)x³ + (95,634)x⁵ - (1,138,500)x⁷ + (7,811,375)x⁹ - (34,512,075)x¹¹ + (105,306,075)x¹³ - (232,676,280)x¹⁵ + (384,942,375)x¹⁷ - (488,494,125)x¹⁹ + (483,841,800)x²¹ - (378,658,800)x²³ + (236,030,652)x²⁵ - (117,679,100)x²⁷ + (46,955,700)x²⁹ - (14,945,040)x³¹ + (3,764,565)x³³ - (740,259)x³⁵ + (111,150)x³⁷ - (12,300)x³⁹ + (945)x⁴¹ - (45)x⁴³ + x⁴⁵ = A

where:



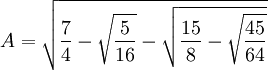
To show that Van Roomen had a solid understanding of this monstrous equation, he observed the following:

(a) If:



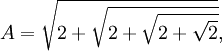
Then:



(b) If:



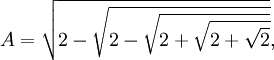
Then:



(c) If:



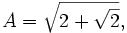
Then:



This problem was mentioned in a meeting between the Dutch ambassador and the King Henry IV of France. The Dutch ambassador had noted that not a single French mathematician had been listed in van Roomen's survey of the great mathematicians.

King Henry IV presented the problem to François Viète who was able to solve it. Viète's solution is historically significant because he not only demonstrated how trigonometry can be used to solve algebraic equations, he also showed that this problem possessed 45 different solutions. This result was important in helping to establish the Fundamental Theorem of Algebra.

How did Viète solve it? I will show his solution in my next blog.

References

• Eli Maor, Trigonometric Delights, Princeton Paperbacks, 1998
• Jean-Pierre Tignol, Galois' Theory of Algebraic Equations, World Scientific, 2001