Friday, June 17, 2005
Bezout's Identity for Gaussian Integers
Bezout's Identity states that the greatest common denominator of any two integers can be expressed as a linear combination with two other integers. For example, because we know that gcd(2,3)=1, we also know that 1 = 2(-1) + 3(1). The proof for rational integers can be found here.
Bezout's Identity is one of three main ideas that are required in order to prove unique factorization. The other two ideas you need are a Division Algorithm, which I detailed in my last blog, and Euclid's Lemma, which I will discuss in a future blog.
Before discussing Bezout's Identity, we will need a lemma that shows that the notion of greatest common denominator applies to Gaussian Integers.
Using the Division Algorithm for Gaussian Integers and Euclid's method for greatest common denominators, we are set. The idea behind Euclid's Method is to do a continuous number of divisions.
Let's assume that we have a,b. First, we divide a by b and get a remainder which I will call r1. Then we divide b by r1 and we get a second remainder which I will call r2. We can keep repeating this until eventually we get a remainder which is 0. We know that this will happen because each remainder is guaranteed by the Division Algorithm to be smaller than the remainder before. After at most b iterations, we will reach a remainder of 0.
Euclid's Method tells us that the last ri value we use is the remainder. It is guaranteed to be at least 1. To make the idea behind this lemma as clear as possible, I will throw out one very simple lemma:
Lemma 1: d divides a, d divides b , a = b + c, then d divides c.
(1) d divides a → there exists A such that a = dA.
(2) d divides b → there exists B such that b = dB
(3) a = b + c → c = a - b = d(A - B)
QED
Lemma 2: For any two Gaussian Integers, it is possible to find the greatest common denominator.
(1) Let α, β be two Gaussian Integers.
(2) We know that there exists η1,δ1 such that:
α = η1β + δ1 and 0 ≤ δ1 which is less than β
(3) β = η2*δ1 + δ2
(4) And: δ1 = η3*δ2 + δ3
(5) We can keep repeating this until eventually we get:
δn-3 = ηn-1 * δn-2 + δn-1
δn-2 = ηn * δn-1 + δn
δn-1 = ηn+1* δn
(6) We know that we eventually get to this point since Norm(δi+1) is always less than the Norm(δi) by the Division Algorithm.
(7) Now, we know that δn divides δn-1 by Step #5. We also know that δn divides δn-2 and therefore, it also divides δn-3 and so on up to β and then α. In other words, it is a common divisor for α and β. [By Lemma 1]
(8) But we also know that if a certain value γ divides both α and β, then it will necessarily divide δ1 and that it will also necessarily divide δ2 and so on. [Again, by Lemma 1]
(9) In other words, we have proven that δn is the greatest common divisor.
QED
Corollary: All quadratic integers that are characterized by a Division Algorithm possess a greatest common denominator.
This is true since all the arguments above only assume a Division Algorithm.
QED
Here is the proof for Bezout's Identity:
Lemma 3: Let α, β be Gaussian Integers. Then there exist two other Gaussian Integers, let's say, ζ, η such that gcd(α,β) = ζα + ηβ
(1) Based on Lemma 2, we have the following:
δn-2 = ηn * δn-1 + δn
(2) This can be restated as:
δn = δn-2 - ηn * δn-1
(3) Now, if we let ζ = 1 and γ = -η we have:
δn = ζ * (δn-2) + γ * (δn-1)
(4) Let's define the following:
δ0 = β
δ-1 = α
With this definition, we can view each step as a continuum of different δi values all the way up.
(5) Now, if you look at equation (2), it shows that at each point, any δi can be restated in terms of smaller values of δi-1 and δi-2. So that:
δn = δn-2 - ηn * δn-1 =
δn-2 - ηn * (δn-3 - ηn-1 * δn-2) =
δn-2(1 + ηn*ηn-1) + δn-3(-ηn)
(6) Setting ζ = 1 + ηn * ηn-1, γ = -ηn, we get:
δn = ζ * δn-2 + γ*δn-3
(7) Again, we can take (5) and move it up one using the same equation:
δn = ζ * (δn-4 - ηn-2 * δn-3) + γ * δn-3 =
= δn-3(-ζ *ηn-2 + γ) + δn-4(ζ)
(8) This shows that we can simplify the equation to a 1 smaller number which can be restated as a linear combination.
(9) Eventually, we get to:
δn = ζ * α + η * β
where ζ = some Gaussian Integer value and η = some Gaussian Integer value.
QED
But now, with the proof of Bezout's Identity, we can get Euclid's Lemma as a corollary.
Corollary 3.1: Euclid's Lemma: if π is a prime that divides α * β, then it divides α or it divides β
(1) Assume π doesn't divide α.
Please note: π is selected as the Greek character equivalent of p. I am not using π to represent 3.14....
(2) Then gcd(π,α) = 1. [By definition of gcd, #1]
(3) From Lemma 3, we know that there exists ζ, η such that:
1 = ζ * α + η * π.
(4) Multiplying both sides by β gives us:
β = ζ * α * β + η * π * β
(5) Since π divides α * β, we know that there exists γ such that:
α * β = π * γ
(6) So we have:
β = ζ * π * γ + η * π * β = π * (ζ * γ + η * β)
QED
Corollary 3.2: Euclid's Generalized Lemma: if π divides α1 * α2 * ... * αn, then π divides at least one of the elements in the product.
(1) Let β1 = α2 * ... * αn
(2) Then π divides α1 * β1 which means by Euclid's Lemma that π divides α1 or β1.
(3) If it divides α1, we are done.
(4) If it divides β1, then we set β2 = α3 * ... * αn and repeat the argument.
(5) Eventually, we hit some αi that is divisible by π.
QED
Corollary 3.3 These results apply to all quadratic integers characterized by a Division Algorithm
Again, none of these arguments are specific to Gaussian Integers. They are true of any quadratic integer that has a division algorithm.
QED
Thursday, June 16, 2005
Division Algorithm for Gaussian Integers
In today's blog, I will show how using the norm function, it is possible to arrive at a Division Algorithm for Gaussian Integers.
The Division Algorithm for rational integers is based on the Well-Ordering Principle and can be found here. It states that whenever we divide one integer by another integer, we are left with a quotient and remainder that are both integers and which are both unique to the division and the remainder is guaranteed to be less than the divisor.
In the lemma below I used Greek letters for Gaussian Integers, Latin letters for rational integers, and Z[i] to represent the set of Gaussian Integers.
Lemma: Division Algorithm for Gaussian Integers
Given: α, γ ∈ Z[i]
Then: there exists ζ, δ such that: α = ζγ + δ and Norm(δ) is less than Norm(γ)
(1) There exists a,b,c,d such that:
α = a + bi
γ = c + di
(2) α / γ = (a + bi) / (c + di) = (a + bi)(c - di) / (c2 + d2) =
= (ac - adi + bci - bdi2)/(c2 + d2) =
=(ac + bd)/(c2 + d2) + i[(bc - ad)/(c2 + d2)]
(3) Let r = (ac + bd)/(c2 + d2).
(4) Let s = (bc - ad)/(c2 + d2)
(5) So, α / γ = r + si
(6) And we know that both r,s are rational. We do not know if they are integers.
(7) We know that there are m,n which are integers such that absolute(r - m) ≤ (1/2) and absolute(s - n) ≤ (1/2). [For proof of this see here]
(8) Let ζ = m + ni.
(9) Let δ = α - ζγ → α = ζγ + δ
(10) Norm(δ) = Norm(α - ζγ) =
= Norm(γ[(α/γ) - ζ] = Norm(α/γ - ζ) * Norm(γ) =
= Norm(r + si - [m + ni]) * Norm(γ) =
= Norm(r - m + si - ni) * Norm(γ) =
= Norm([r - m] + [s -n]i) * Norm(γ) =
= [(r - m)2 + (s - n)2] * Norm(γ) ≤ [ (1/2)2 + (1/2)2]*Norm(γ) =
= (1/2)*Norm(γ) which is less than Norm(γ)
QED
Wednesday, June 15, 2005
Properties of Gaussian Integers
When we look at standard integers, officially called rational integers, we recognize that most of their properties are based on the Well Ordering Principle. This is the idea that for any given set of nonnegative integers, there is always one that is the smallest. If any one is interested in seeing the proofs related to the Well Ordering Principle and rational integers, you can check out here.
With Gaussian Integers, we are looking at a domain where the Well Ordering Principle does not apply. In the case of rational integers, it was clear that they can be thought to extend across a number line. Gaussian Integers, in contrast, extend across two number lines: a rational integer line and an i integer line.
For this reason, the previous proofs do not apply. We will need to come up with new proofs for the basic ideas. The basic idea of unique factorization is built from the following ideas:
(1) A Division Algorithm: What assumptions can we make about division? What assumptions can we make about quotients and remainders? See here for the algorithm with regard to rational integers. See here for the algorithm with regard to Gaussian Integers.
(2) Bezout's Identity: This is the idea that the greatest common denominator of any two integers can be represented as an equation based on two other integers. See here for the identity with regard to rational integers. See here for the proof of the identity with regard to Gaussian Integers.
(3) Euclid's Lemma: This is the idea that if a prime integer divides the product of two integers, then either it divides the first integer or it divides the second. See here for the proof of Euclid's Lemma regarding rational integers. See here for the proof with regard to Gaussian Integers.
Unique Factorization, it turns out, comes directly from Euclid's Lemma. As a convention, I will use Greek letters to represent Gaussian Integers and Latin letters to represent Rational Integers. So that: α = a + bi where α is a Gaussian Integer and a,b are rational integers.
There is one trick that we need to do in addition to using norms. We need to talk about the idea of associates.
Definition: Associates: Two numbers are associates if one is equal to the other multiplied by a unit.
The Gaussian Integers have four different units: i,-i,1,-1 (see Corollary 4.1, here). So, we can see that 4, -4, 4i, and -4i are all associates of each other. So, when we are talking about unique factorization of primes, we are considering prime associates to be the same prime. So, when we prove unique factorization, we are really proving a unique set of prime-associates.
Theorem: Gaussian Integers posess Unique Factorization.
(1) We know that all non-zero, non-units are either primes or composed of primes. [By the definition of primes]
(2) Let's assume that a given number is made of two different sets of primes.
(4) So α = β1*β2*...*βr = γ1*γ2*...*γs
(5) Now each prime βi must necessarily match a prime in γj by Euclid's Generalized Lemma. [See here for the proof of Euclid's Generalized Lemma for Gaussian Integers]
(6) But we can make the same argument for all βi so there must be an equal prime or associate in the set of γj.
(7) But then, there cannot be any prime left over since if we divide all the βi, then we are left with a unit.
(8) So, we have proven that the set of primes is necessarily unique.
QED
Corollary: All Euclidean Integers posessess unique factorization.
(1) By definition, all Euclidean Integers are characterized by a Division Algorithm. [See here for review of Euclidean Integers]
(2) All Euclidean Integers are therefore also characterized by Euclid's Generalized Lemma. [See here for the proof.]
(3) With these two results, the same arguments above apply to all Euclidean Integers.
QED
Friday, June 10, 2005
Norms for Gaussian Integers
Carl Friedrich Gauss and Leonhard Euler both proposed extensions of integers that used irrational numbers that they were able to use to make elegant proofs for Fermat's Last Theorem.
A set of integers is extended by including additional values. In standard integers, the values are positive and negative whole numbers and 0. In extended integers, we can include additional values such as i, 5i, etc. Gaussian integers include all of the standard integers plus the addition of multiples of i. In other words, a Gaussian Integer is defined by two integers: a,b where each Gaussian integer can be represented a + bi.
In my previous blog, I spoke about using a special function, the norm, to reason about Gaussian Integers. I will now present a few interesting lemma. To distinguish between Gaussian Integers and standard integers, I will use Greek letters to represent Gaussian Integers and Latin letters to represent standard integers:
Lemma 1: Norm(α) = 0 if and only if α = 0
(1) Norm(α) = Norm(a + bi) = (a + bi)(a - bi) = a2 + b2
(2) But if a ≠ 0, then a2 + b2 > 0.
(3) And the same holds true if b ≠ 0.
QED
In mathematical notation, the conjugate of a Gaussian Integer is represented with an overline over it. So, if α is a Gaussian Integer, then: α is the conjugate. This is important since the norm is equal to a Gaussian Integer multiplied by its conjugate.
Lemma 2: (α * β) = α * β
(1) (α * β) = (a + bi) * (c + di) = (ac - bd) + i(ad + bc)
(2) So, α * β = (ac - bd) - i(ad + bc)
(3) And, α * β = (a - bi) * (c - di) = (ac - bd) - i(ad + bc).
QED
Lemma 3: Norm(α*β) = Norm(α) * Norm(β)
(1) Norm(α*β) = (α*β)(α*β) =
(2) = α*β*α*β [ From Lemma 2 ]
(3) = (α*α)(β*β)
(4) =Norm(α)*Norm(β)
QED
In standard integers, we speak about 1, -1 as being units -- that is, numbers which divide all other numbers. This is important because when we are discussing prime numbers or relatively prime numbers, we are necessarily talking about numbers other than 0 or the units.
In the realm of Gaussian Integers, a unit is defined as any number that divides 1.
Lemma 4: if α is a unit, then Norm(α) = ±1
Proof:
(1) If α is a unit, then there exists another value β such that α * β = 1.
(2) Now, Norm(α * β) = Norm(1) = 1 = Norm(α) * Norm(β)
(3) But if either Norm(α) ≠ ±1 or Norm(β) ≠ ± 1, then the Norm(α * β) couldn't equal 1 (since there are no other rational integers that multiply to 1).
(4) So, Norm(α) must equal ± 1.
QED
Corollary 4.1: The only units for Gaussian Integers are i,-i,1,-1
Proof:
(1) N(i) = i*(-i) = 1 [See Definition 2 here for details if needed]
(2) N(-i) = (-i)*i = 1 [See Definition 2 here for details if needed]
(3) N(1) = 1*1 = 1 [See Definition 2 here for details if needed]
(4) N(-1) = (-1)*(-1) = 1 [See Definition 2 here for details if needed]
(5) If N(α) is a unit where α = a + bi, then:]
(a + bi)(a - bi) = a2 + b2 = 1
(6) But this can only occur if a=0 or b=0 since:
(a) if a ≠ 0 and b≠ 0
(b) Then abs(a) ≥ 1 and abs(b) ≥ 1
(c) And, a2 + b2 ≥ 2
(7) But then the only possible units are 1, -1, i, -i
(a) if a = 0, then b = ± 1 so that we have α = i or α = -i
(b) if b=0, then a = ± 1 so that we have α=1 or α=-1
QED
We are now ready to define a Gaussian Prime. A Gaussian prime is any Gaussian Integer which is not 0 or a unit which is only divisible by a itself or a unit.
Lemma 5: if Norm(α) is a standard prime, then α is a prime.
(1) So, we start with Norm(α) = p which is a standard prime.
(2) Assume α is not a prime.
(3) Then there exists two Gaussian Integers: β, γ that are not units such that: α = β * γ.
(4) And then Norm(β * γ) = Norm(β) * Norm(γ) [By Lemma 3 above]
(5) Since Norm is a mapping function to standard integers, we know that there exists b,g such that:
b = Norm(β)
g = Norm(γ)
(6) We know that Norm(β * γ) = p and we know that b,q ≠ 1 [By Lemma 4, since they are not units]
(7) But then p = b * g which is impossible since p is a prime.
(8) Therefore, we reject our assumption in (2).
QED
Lemma 6: (α/β) = α / β
(1) There exists a,b,c,d such that α = a + bi. β = c + di.
(2) (α/β) =




[From Lemma 2 above]

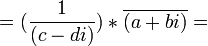
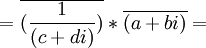
= (a + bi) / (c + di)
QED
Lemma 7: Norm(α / β) = Norm(α) / Norm(β)
(1) Norm(α / β) = (α / β) * (α / β) [Definition of Norm]
= (α / β) * α / β = Norm(α) / Norm (β)
QED
Corollary 7.1: If α divides β, then Norm(α) divides Norm(β)
Proof:
(1) Assume that α divides β.
(2) Then there exists an integer γ such that γ = β / α.
(3) By the definition of a norm (see here), Norm(γ) is a rational integer.
(4) But then Norm(β)/Norm(α) = Norm(γ) which means that Norm(α) must divide Norm(β).
QED
In my next blog, I will prove that Gaussian Integers possess unique factorization.
The lemmas from today's blog were taken from an excellent book by Harold M. Stark called An Introduction to Number Theory .
Thursday, June 09, 2005
Unique Factorization
Unique factorization is the idea that a given whole number consists of a unique set of primes. For every set of unique primes, there is one and only one number that can be built. For every number, there is one and only one unique set of primes.
Before Gauss, this idea was probably not interesting to mathematicians because it is so clearly true in the case of integers. On the other hand, when Leonhard Euler presented his proof for Fermat's Last Theorem n=3, he introduced a new set of integers in the form of a + b√-3. This was a brilliant proof and yet he made a mistake. He assumed that unique factorization automatically applied. It was Gauss's insight that this assumption requires proof.
Gauss took the idea of unique factorization very seriously when he proposed what are today called Gaussian Integers. Using i-notation, where i is the square root of -1, a Gaussian integer is defined by the set of all values that can be created by a + bi where a,b are integers. It is also represented by the form Z[i]. Using this notation, Euler's proof used integers of the form Z[√-3].
The interesting idea behind Gaussian Integers is that any theorem which is true of all Gaussian Integers is also true of all integers since integers are Gaussian Integers wheren b = 0.
But how does one reason with Gaussian Integers? On the surface, it doesn't look like they will be offer any insights beyond the standard integers. In fact, it seems, on the surface, that reasoning about them will be more difficult since they themselves are more complicated. Using standard integers, we know that 5 is a prime. But in the realm of Gaussian Integers, it is not a prime since
5 = (2 + i)(2 - i) = 4 + 1 = 5.
Gaussian Integers are interesting because they allow us to factor equations in interesting ways. For example, the equation x4 + y4 can now be factored into (x2 - y2i)(x2 + y2i). Without Gaussian Integers, there wouldn't be an easy factoring. This was really Euler's motivation for extending the integers since he was able to break x3 + y3 into a form such as:
(x + y)(x + ay)(x + by).
Coming up with proofs about Gaussian integers becomes interesting with the introduction of a special function called the norm. The norm is a mapping function that maps any Gaussian Integer to a standard integer. The norm is important because it enables to us to define Gaussian primes and because it then enables us to establish unique factorization for Gaussian Integers.
How does one find a mapping function that is guaranteed to convert any Gaussian Integer to a standard integer? The answer comes from the following mathematical equation:
(a + b)(a - b) = aa -ab +ab - bb = a2 - b2
In the case of i, this becomes:
(a + bi)(a - bi) = a2 - (b2)(-1) = a2 + b2.
The form a - bi is called the conjugate of the Gaussian Integer. Hardy and Wright (see reference below) define the norm as the product of a Gaussian Integer with its conjugate. For purposes of my discussion on Gaussian integers, I will use the Hardy and Wright definition (I should point out that this is not the standard definition of norm, see here; I will revisit this point at a later time). The important point behind the norm is that it is a mapping between the Gaussian integers and the rational integers that allows us to reason about the Gaussian integers (see here for an example of using the norm for Gaussian integers to establish a division algorithm for Gaussian integers.)
For example, the norm of 5i is (0 + 5i)(0 - 5i) = 25. Interestingly, the norm of -5i is also 25. This is important because it shows that the norm is not a one-to-one mapping. All Gaussian integers and their conjugates share the same norm.
In summary, I offer the following definitions for Gaussian Integers:
Definition 1: Conjugate of a Gaussian Integer
The conjugate of a Gaussian Integer a+bi is a-bi and likewise, the conjugate of a Gaussian Integer a-bi is a+bi.
Definition 2: Norm of a Gaussian Integer: N(α) = α * α
Following Hardy and Write (see article by Eric Weisstein for details), the norm of a Gaussian integer α is α multiplied by its conjugate α, that is, the norm N(α) = α * α.
Over the next set of blogs, I will show how norms allow us to establish unique factorization for Gaussian Integers. My next blog will cover some basic ideas about Gaussian Integer norms.
References
- G. H. Hardy, E. M. Wright, Introduction to the Theory of Numbers, Oxford University Press, 1980
- Eric Weisstein, "Gaussian Integer", MathWorld,
Tuesday, June 07, 2005
Carl Friedrich Gauss
 Carl Friedrich Gauss was born on April 17, 1777 to poor, working class parents in Brauschweig, Germany. His mother had been a maid and his father had been a laborer and handyman. His father, it is said, did not appreciate Gauss's abilities or his later accomplishments.
Carl Friedrich Gauss was born on April 17, 1777 to poor, working class parents in Brauschweig, Germany. His mother had been a maid and his father had been a laborer and handyman. His father, it is said, did not appreciate Gauss's abilities or his later accomplishments.Gauss is considered to be one of the three greatest mathematicians of all time. The other two being Archimedes and Sir Isaac Newton. His accomplishments are so vast that this blog will only be a brief glimpse. For those interested in greater details, please check out the reference list at the end of this blog.
Gauss showed indications of mathematical genius very early. According to a popular story, he noticed a mistake in his father's calculations when he was only 3 years old. Later, he supposedly taught himself to read and by the time he was 8, he was already astounding people by his mathematical abilities. For example, there is a well known anecdote where a teacher gave his students an assignment to add up a series of 100 numbers. Instantly, Gauss said that he had completed the exercise (the story goes that he had figured that 100 numbers could be determined by the equation n(a+b)(1/2)=50(a+b) where n=100, a = the first digit in the sequence and b = the last digit in the sequence.)
Gauss's teachers would lend him books and try to help him along with his independent studies of the subject. In 1788, at the age of 11, he entered the Gymnasium, a college preparatory school. In 1792, at the age of 14, he received a stipend from the Duke of Brunswick which made him financially independent for the next 16 years and it was that year that he entered Brunswick College.
He entered the University at Gottigen in 1795 and became famous in 1796 at the age of 19 with his discovery on March 30 of a method for constructing a heptadecagon (a regular 17-sided polygon) using only a compass and ruler. He was so excited by this that he requested that a heptadecagon be placed on his tombstone. For his doctoral thesis, he proved the fundamental theorem of algebra which states that all polynomials of degree n have n different solutions in the domain of complex numbers.
Gauss's other discoveries include the law of quadratic reciprocity, Gaussian distribution, modular arithmetic, non-Euclidean geometry, the prime number theorem, the systematization of number theory, and the method of least squares. Gauss worked on many of these discoveries completely on his own without any collaborators.
Gauss also had a strong interest in astronomy. In 1801, the planetoid Ceres was first sighted. Gauss studied data abouts its orbit and was able to predict a second possible sighting which was confirmed on December 31, 1801. In 1805, he became Director of the Observatory in Gottingen.
Despite his fame in mathematics, Gauss never became a mathematics professor and only attended one math conference. It was said that he strongly disliked teaching. When his good friend Farkas Bolyai told him that his son has come up with a non-Euclidean geometry, Gauss responded:
"To praise it would amount to praising myself. For the entire content of the work ... coincides almost exactly with my own meditations which have occupied my mind for the past thirty or thiry-five years."
Gauss's personal life was filled with tragedy. His first wife died in 1809 and a few years later, his first son died. It was said that throughout his life, he never overcame the sadness of this event. His second wife died in 1831 after a long illness. He never married after that. He died on February 23, 1855.
Gauss did not publish most of his discoveries. They were published after his death.
His face can be found on the German Deutche mark from 1989 until 2001:
References for this blog:
Saturday, June 04, 2005
Euler's Mistake
In Leonhard Euler's original proof for Fermat's Last Theorem n=3, he made a mistake. For anyone interested in seeing the details of the proof, it is perhaps comforting to know that a genius like Euler was capable of getting the details wrong. The details of this blog are based on Harold M. Edwards's book, Fermat's Last Theorem.
The mistake came when Euler tried to prove the key lemma of his proof. In his published proof, Euler attempted to prove this lemma using imaginary numbers. Euler is credited with the invention of the notation for imaginary numbers and one of the most fascinating equations ever derived which is known as Euler's Identity:
eiπ=-1
So, it is not too surprising that he would apply this method to Fermat's proof. It is also very interesting to note that a less innovative method can be constructed based on Euler's other work. This is what I did in the proof that I presented earlier.
Also interesting is the fact that this technique turns out to be a very important innovation which makes possible additional proofs for n=5, n=7, and Kummer's proof for regular primes.
Euler tries to prove the following lemma:
Lemma: Given that p2 + 3q2 is a cube, show that there exist a,b such that p = a3 - 9ab2 and q = 3a2b - 3b3.
Here's Euler's idea. What if we presuppose that there exists numbers of the form:
a + b√-3
If we allow that these numbers exist, then we have the following equation:
p2 + 3q2 = (p + q√-3)(p - q√-3)
So far so good. Mathematicals in general will allow any extension of numbers as long as the extension is logically consistent. The rational numbers extend the integers. Real numbers extend the rational numbers and Complex numbers extend the real numbers.
Euler proceeds to show that the two complex numbers (p + q√-3, p - q√-3) are relatively prime to each other. His proof here also works. I will add the details for this proof later.
He then concludes that the two complex numbers must, therefore, be cubes based on the reasoning of the Relatively Prime Divisor Lemma. This is the mistake!
In modern notation, Euler assumed that Z[√-3] was characterized by unique factorization. This is not completely correct. In actual fact, Z[(-1 + √-3)/2] is characterized by unique factorization. I go into more detail on this subject in my blog about Euclidean integers. If you are not familiar with quadratic integers, start here.
This result would be greatly extended by Carl Friedrich Gauss.
Friday, June 03, 2005
Fermat's Last Theorem: n = 3 : last lemma needed for proof
Lemma: For all odd numbers, there exists a value n such that the number is equal to 4n ± 1 with n greater than 0.
(1) Let S = the set of all odd numbers representable by 4n + 1 or 4n - 1
(2) We know that 1 is an element of this set since 1 = 4(0) + 1
(3) We can then presuppose that there is some value v such that all odd numbers less than or equal to v are describeable by 4n + 1 or 4n - 1. We know that v is greater or equal to 1
(4) Now, we will prove that if v is of the form 4n + 1 or 4n - 1, then v + 2 is also of this form.
Case I: v is of the form 4n + 1
v + 2 = 4n + 1 + 2 = 4n + 3 = 4(n+1) - 1
Case II: v is of the form 4n - 1
v + 2 = 4n - 1 + 2= 4n + 1
(5) By the Principle of Mathematical Induction, we have proven this lemma.
QED
Thursday, June 02, 2005
Fermat's Last Theorem: n = 3 : multiplication with a2 + 3b2
This is part of the larger proof for Fermat's Last Theorem: n=3 which was first published by Leonhard Euler.
Lemma: Multiplying two polynomials of the form a2 + 3b2 results in a polynomial with the same form.
(a2 + 3b2)(c2 + 3d2) = a2 (c2 + 3d2) + 3b2 (c2 + 3d2) =
= a2c2 + 3a2d2 + 3b2c2 +9b2d2 =
= a2c2 - 6abcd + 9b2d2 + 3a2d2 + 6abcd + 3b2c2 =
= (ac - 3bd)2 + 3(ad + bc)2
QED
Wednesday, June 01, 2005
Fermat's Last Theorem: n = 3: Division of a2 + 3b2 by 2
Lemma: if 2 divides a polynomial of form a2 + 3b2, then 4 also divides the polynomial and this division by 4 results in another polynomial of the same form.
In other words, we will prove two propositions:
- if 2 divides a2 + 3b2, then 4 also divides it.
- if 4 divides a2 + 3b2, then there exists c,d such that a2 + 3b2 = 4*(c2 + 3d2)
(1) We know that a,b have the same parity (they are both odd or they are both even). Otherwise, a2 + 3b2 would not be divisible by 2
(2) If they are both even, then it is easy to show that 4 divides a2 + 3b2 and that the result is of the same form:
(a) There exists c,d such that a = 2c and b = 2d
(b) a2 + 3b2 = (2c)2 + 3(2d)2 = 4(c2 + 3d2)
(3) So, we can assume that they are both odd.
(4) Now, there exists m,n such that a = 4m ± 1, b = 4n ± 1 [See here for proof]
(5) From this, we know that 4 divides either a + b or a - b
(6) I will now show that in both cases, the lemma is proven.
Case I: 4 divides a + b
(a) First, 4(a2 + 3b2) = (12 + 3*12)(a2 + 3b2) = (a - 3b)2 + 3(a + b)2 [See here for proof]
(b) Since a - 3b = (a + b) - 4b, we know that 4 divides a - 3b
(c) So, this gives us that 42 divides (a - 3b)2 + 3(a + b)2 which also means that:
4 divides a2 + 3b2 [Since 42 divides (a - 3b)2 + 3(a+b)2 implies 42 divides 4(a2 + 3b2)]
(d) Since 4 divides a - 3b and a + b, we know that there exists u,v such that: u = (a - 3b)/4 and v = (a + b)/4
(e) 4(u2 + 3v2) = 4{[(1/4)(a - 3b)]2 + 3[(1/4)(a + b)]2} =
= (1/4)(a2 + 9b2 + 3a2 + 3b2) =
= (1/4)(4a2 + 12b2) = a2 + 3b2
Case II: 4 divides a - b
(a) The argument here is the same as for case I except that we set 4(a2 + 3b2) = (12 + 3*(-1)2)(a2 + 3b2) = (a + 3b)2 + 3(a - b)2 [See here for proof.]
(b) Then after proving that 42 divides this result, we let u = (1/4)(a + 3b) and let v = (1/4)(a - b).
(c) Then 4(u2 + 3v2) = a2 + 3b2
QED
Tuesday, May 31, 2005
Fermat's Last Theorem: n = 3 : Division with a2 + 3b2
This result is needed for the proof of Fermat's Last Theorem for n=3 that was first presented by Leonhard Euler. For those interested in seeing the entire proof, please start here.
Lemma: if a prime of form p2 + 3q2 divides a2 + 3b2, then there exists c,d such that:
a2 + 3b2 = (p2 + 3q2)(c2 + 3d2)
(1) There exists f such that a2 + 3b2 = (p2 + 3q2)f.
(2) (pb - aq)(pb + aq) = p2b2 - a2q2 + (3q2b2 - 3q2b2) =
= p2b2 + 3q2b2 - 3q2b2 - a2q2 =
= b2 ( p2 + 3q2 ) - q2 ( a2 + 3b2 )
(3) Now the prime p2 + 3q2 divides either pb - aq or pb + aq since:
(pb - aq)(pb+aq) = (p2 + 3q2)(b2 - q2f) [From Euclid's Lemma and steps (1), (2)]
(4) So that there exists a value F such that:
(p2 + 3q2)F equals either pb + aq or pb - aq
(5) Now, from multiplication of polynomials with this form, we know that:
(p2 + 3(±q)2)(a2 + 3b2) = (pa ± 3qb)2 + 3(pb ± aq)2
(6) So, p2 + 3q2 divides pa ± 3qb since:
(pa ± 3qb)2 = (p2 + 3q2)(a2 + 3b2) - 3(pb ± aq)2 =
(p2 + 3q2)[(a2 + 3b2) - 3(F)2]
(7) So, there exists c,d such that:
pa ± 3qb = c(p2 + 3q2)
pb ± aq = d(p2 + 3q2)
(8) Which means that:
(pa ± 3qb)2 + 3(pb ± aq)2 =
(c * (p2 + 3q2))2 + 3[d * (p2 + 3q2)]2
(9) Putting it altogether means that:
(a2 + 3b2) divided by (p2 + 3q2) =
(pa ± 3qb)2 + 3(pb ± aq)2 divided by (p2 + 3q2)2 [From step (5)]
= [c * (p2 + 3q2)]2 + 3[d * (p2 + 3q2)]2 divided by (p2 + 3q2)2 =
c2 + 3d2
QED
Monday, May 30, 2005
Fermat's Last Theorem: n = 3: More a2 + 3b2
Lemma: if a2 + 3b2 has an odd factor that is not of this form, then the quotient has an odd factor which is not of this form.
In other words, given the following:
- There exists f which is a factor of a value a2 + 3b2
- f does not have the form p2 + 3q2
- A value F such that fF = a2 + 3b2
- A value f' such that f' divides F and such that it does not have the form p2 + 3q2
(1) So there exists f,g such that fg = a2 + 3b2, f is odd and f is not in the form p2 + 3q2
(2) Let's assume that all of the odd factors of g have the form p2 + 3q2
(3) Now g = a series of primes p1 * p2 * ... * pn [By the Fundamental Theoreom of Arithmetic]
(4) In this series, we can replace all instances of 2 with instances of 4.
(a) We know that if 2 divides a2 + 3b2, then 4 divides it. [See here for proof]
(b) We know that f is odd so each instance of 4 necessarily divides g
(5) Now we can divide all instances of 4 from g and from a2 + 3b2 and still have a result in the form of p2 + 3q2. [See here for proof]
(6) Likewise, we can divide all odd primes from g since we are assuming that all odd factors take the form p2 + 3q2. [The proof is found here.]
(7) But then this leaves f = p2 + 3q2 which is a contradiction.
(8) Therefore, we reject our assumption.
QED
Sunday, May 29, 2005
Fermat's Last Theorem: n = 3: a2 + 3b2
In today's blog, I will present a lemma that illustrates one of the surprising properties of the above formula.
This blog will continue the details of the proof that was begun in a previous blog.
Lemma: If gcd(a,b)=1, then every odd factor of a2 + 3b2 has this same form.
In other words, for every odd factor of a2 + 3b2, there exists c,d such that the odd factor = c2 +3d2
(1) Let x be a positive, odd factor of a2 + 3b2
(2) Then, there exists a value f such that:
a2 + 3b2 = xf
(3) We can assume that x is greater than 1 (since if x = 1 it's only factor is itself and 1 = 12 + 3(0)2.)
(4) There exists integers m,n such that:
a = mx ± c
b = nx ± d
where c,d can be positive or negative.
(5) Now, we can assume that c,d have absolute values that are less than (1/2)x.
(a) From the Division Algorithm (see Theorem 1, here), we know that c is less than x.
(b) Assume that c ≥ (1/2)x
(c) c' = x - c = -(c - x)
(d) a = mx + c = (m+1)x + c - x = (m+1)x - (x - c) = (m+1)x - c'
(e) abs(c') is less than (1/2)x since c' = x - c
(6) From step #4, we have:
a2 + 3b2 =
(mx ± c)2 + 3(nx ± d)2 =
m2x2 ± 2mxc + c2 + 3n2x2 ± 6nxd + 3d2 =
= x(m2x ± 2mc + 3n2x ± 6nd) + c2 + 3d2
(7) So x divides c2 + 3d2 since from step #1, since x is a factor of a2 + 3b2.
(8) So, there exists y such that:
c2 + 3d2 = xy
(9) Now from step #5 above, we have:
xy = c2 + 3d2 is less than [(1/2)x]2 + 3[(1/2)x]2 = (1/4)x2 + (3/4)x2 = x2.
(10) Now, we can conclude that y is less than x from:
(a) Since c2, d2 are nonnegative, it follows that xy is nonnegative.
(b) From step #9, xy is less than x2
(c) Since x is positive, the only way that this can be true is if y is less than x.
(11) We also know that c2 + 3d2 ≠ 0 because:
(a) Assume c2 + 3d2 = 0.
(b) Then c=0, d=0 since c2 and 3d2 are both nonnegative.
(c) But then: a = mx, b = nx and x divides both a,b.
(d) Which contradicts gcd(a,b)=1 so we reject our assumption.
(12) Let g = gcd(c,d). We know there exists C,D such that c = gC, d=gD, gcd(C,D)=1. [From the properties of greatest common denominators]
(13) Now we also know that g2 divides y because:
(a) xy =c2 +3d2 = (gC)2 + 3(gD)2 = g2(C2 + 3D2)
(b) Assume there is a prime p that divides g but doesn't divide y.
(c) Then p divides g and p divides x
(d) Then, there exists X,G where x = Xp, g = Gp
(e) And, p divides a and b since
a = mx + c = mpX + GpC = p(mX + GC)
b = nx + d = npX + GpD = p(nX + GD)
(f) But this is impossible since a,b are coprime.
(g) So, there is no prime p which divides g but does not divide y.
(h) Which proves that g divide y and further that g2 divides y
(14) Since g2 divides y, there exists z such that:
y = g2z
(15) Now, it follows that there exist C,D such that:
xz = C2 + 3D2 where gcd(C,D)=1
(a) xy = g2(C2 + 3D2) [from step #13a above]
(b) gcd(C,D) = 1 [from step #12 above]
(c) Then substituting z from step #14 gives us:
xz = C2 + 3D2
(16) Now we have enough to conclude that x is of the form p2 + 3q2
(a) Assume that x is not of this form.
(b) From step #15, we have xz = C2 + 3D2 where gcd(C,D)=1.
(c) Then there must exist w such that w divides z and w is not of the form p2 + 3q2 [See here
for the proof of this lemma]
(d) Now, w ≠ 1 since 1 = 12 + 3(0)2
(e) So, w is smaller than z [since w is greater than 1 and w divides z]
(f) But then w is less than x [since z is less than y (step #14, since y = g2z) and y is less than x (step #10)]
(g) But now, we have proven that the existence of x proves the existence of a smaller factor w which divides a smaller value of the same form.
(h) We can use the same argument to presuppose a value w' which is smaller than w and another value w'' which is smaller than w'. In other words, we have a contradiction by the method of infinite descent.
QED
Saturday, May 28, 2005
Fermat's Last Theorem: n= 3: Key Lemma
In my opinion, this obscure lemma is the most beautiful part of the proof. It is surprisingly elegant.
Here is the lemma:
Lemma: Given that there exist p,q with the following properties:
(a) gcd(p,q)=1 (gcd = greatest common denominator)
(b) p,q have opposite parities (one is odd, one is even)
(c) p2 + 3q2 is a cube
Then there exists a,b such that:
(a) p = a3 - 9ab2
(b) q = 3a2b - 3b3
(c) gcd(a,b)=1
(d) a,b have opposite parities
Proof:
(1) Let u3 = p2 + 3q2. [Since we know that p2 + 3q2 is a cube.]
(2) We know that u is odd since p,q have opposite parities [that is, one is odd, one is even].
(3) We know then that u must be of the form a2 + 3b2. [Since any odd factor would also have to have the same form, see here for the lemma regarding odd factors of p2 + 3q2]
(4) Now, (a2 + 3b2)3 = (a2 + 3b2)[(a2 - 3b2)2 + 3(2ab)2]
since (a2 + 3b2)2 = a4 + 6a2b2 + 9b4 =
= a4 + 12a2b2 - 6a2b2 + 9b4 =
(a2 - 3b2)2 + 3(2ab)2
(5) And, (a2 + 3b2)[(a2 - 3b2)2 + 3(2ab)2] =
[ a(a2 - 3b2) - 3b(2ab)]2 + 3[a(2ab)+b(a2-3b2)]2 [See here for the proof.]
(6) And: [ a(a2 - 3b2) - 3b(2ab)]2 + 3[a(2ab)+b(a2-3b2)]2 =
= [a3 - 3ab2 - 6ab2]2 + 3(2a2b + a2b - 3b3)2 =
=[a3 -9ab2]2 + 3(3a2b - 3b3)2.
(7) Which combined with step (1) gives us:
p2 + 3q2 = [a3 -9ab2]2 + 3(3a2b - 3b3)2
(8) Which means that we could define a,b such that:
p = a3 -9ab2.
q = 3a2b - 3b3.
gcd(a,b)=1 [since otherwise, any common factor would divide p and q].
(9) We also know that a,b have opposite parities since:
(a) If a,b are both odd, then, p is even since p = odd - odd and q is even since q = odd - odd which is impossible since p,q have opposite parities.
(b) If a,b are both even, then p is even since p = even - even and q is even since q = even - even which is impossible.
QED
Friday, May 27, 2005
Fermat's Last Theorem: n = 3: Step 4
Lemma: Given the following conditions:
(a) x,y,z is a solution to x3 + y3 = z3
(b) two values of x,y,z are derived from p+q,p-q
(c) p,q coprime
(d) p,q opposite parity
(e) p,q positive
(f) 2p*(p2 + 3q2) is a cube.
(g) gcd(2p,p2 + 3q2) = 3
Then:
There exists a smaller solution A,B,C such that A3 + B3 = C3.
(1) First, we note that 3 divides p but not q. Since 3 divides 2p [see #g] and p,q are coprime [see #c].
(2) So, there exists s such that:
p = 3s and
2p * (p2 + 3q2) = 2p*(3s*3s + 3q2) = 2*3s*(3*3s2 + 3q2) =
= 32*2s(3s2 + q2)
(3) Now 32*2s, 3s2 + q2 are relatively prime since:
(a) 3 doesn't divide q [step #1]
(b) so 3 doesn't divide 3s2 + q2
(c) Since p=3s [#2], s is the same parity as p which means that s,q have opposite parity [see #d in given].
(d) But if s,q have opposite parity, then 2 doesn't divide 3s2 + q2 since it must be odd.
(e) Finally, gcd(s,q)=1 since gcd(p,q)=1. [see #c in the given]
(4) So, 32*2s, 3s2 + q2 are cubes [By Relatively Prime Divisor Lemma] since 32*2s(3s2 + q2) = 2p * (p2 + 3q2) [see #2] and 2p * (p2 + 3q2) is a cube [see #f in given].
(5) Then, there exists a,b such that:
q = a3 - 9ab2
s = 3a2b - 3b3
gcd(a,b)=1
since:
gcd(q,s)=1 [See #3e above]
q,s have opposite parities [see #3c above]
q2 + 3s2 is a cube [see #4 above]
[See here for the lemma that establishes this]
(6) From, this we can show that 2b, a-b, a+b are cubes
(a) a,b have different parity since q,s have different parity [see #3c above] since:(7) But this means there exists A,B,C such that:
Case I: a,b are both even
q = a3 - 9ab2 = even - even = even.
s = 3a2b - 3b3 = even - even = even
which is impossible since q,s have different parity.
Case II: a,b are both odd
q = a3 - 9ab2 = odd - odd = even
s = 3a2b - 3b3 = odd - odd = even.
which is impossible since q,s have different parity.
(b) a + b, a - b are odd since a,b have different parity so 2 is coprime.
(c) b is coprime to a + b and a - b, otherwise, it would divide a which goes against gcd(a,b)=1
(d) a + b, a - b are coprime since any common factor would be odd and divide both a and b since 2a = a + b + a - b and 2b = a + b - (a - b)
(e) 32*2s is a cube [see #4 above] so 32*2s =32*2[3a2b - 3b3] = 33*2[a2b - b3] = 33(2b)(a+b)(a - b) is a cube.
(f) But if 33(2b)(a+b)(a - b) is a cube, then (2b)(a+b)(a - b) is a cube.
(g) But if (2b)(a+b)(a - b) is a cube and gcd(2b,a+b,a-b)=1 [by #6b,#6c,#6d], then by the Relatively Prime Divisor Lemma, 2b, a+b, and a-b are all cubes.
A3 = 2b
B3 = a - b
C3 = a + b
(8) Which means that there is another solutions to Fermat's Last Theorem n=3 since:
A3 = 2b = a + b - (a - b) = C3 - B3
(9) Now, since:
C3 = a + b which is less than s = (3b)(a - b)(a + b) which is less than p = 3s which is less than either x3 or z3 since either z3 = (2p)*(p2 + 3q2) or x3 = (2p) * (p2 + 3q2).
(10) So, a solution here leads necessarily to a smaller solution of FLT n=3.
QED
Thursday, May 26, 2005
Fermat's Last Theorem: n = 3: Step 3
With this step, we enter the heart of the proof for Fermat's Last Theorem n=3. This step is a bit complicated so I will only be able to provide an outline at this point. Later on, I will update this blog and insert all the details.
Lemma: Given the following conditions:
(a) x,y,z is a solution to x3 + y3 = z3
(b) two values of x,y,z are derived from p+q,p-q
(c) p,q coprime
(d) p,q opposite parity
(e) p,q positive
(f) 2p*(p2 + 3q2) is a cube.
(g) gcd(2p,p2 + 3q2) = 1
Then:
There exists a smaller solution A,B,C such that A3 = B3 + C3.
(1) 2p and p2 + 3q2 are cubes. [From Relatively Prime Divisors Lemma]
(2) First, we show that there exists two values a,b such that: [See here for the lemma.]
p = a3 - 9ab2, q = 3a2b - 3b3, gcd(a,b)=1, a,b opposite parity
(3) This gives us that:
2p =2a3 - 18ab2 =(2a)(a - 3b)(a + 3b)
(4) 2a, a - 3b,a + 3b are all coprime.
(a) First, 2a is coprime with a - 3b and a + 3b. Both a - 3b and a + 3b are odd since a,b have opposite parity. If a had a common factor with either, then this factor would also divide b which goes against our assumption.
(b) If any odd prime greater than 3 divides a - 3b and a + 3b, then it must divide a since 2a = a - 3b + a + 3b and it must divide b since 6b
= a + 3b - (a - 3b). But this is impossible.
(c) We already showed that 2 can't divide a - 3b, a + 3b. So all we need to prove is that 3 also can't divide both. If 3 divides both then it divides a since 2a = a - 3b + a + 3b, then it also divides p since p = a3 - 9ab2. But it can't divide p since gcd(2p,p2 + 3q2)=1. So, 3 can't divide both.
(5) So, once again, all three are cubes. [By Relatively Prime Divisors Lemma] so that we have A,B,C such that:
2a = A3
a - 3b = B3
a + 3b = C3
(6) But this gives us another solution to Fermat's Last Theorem: n=3 since:
A3 = 2a = a - 3b + a + 3b = B3 + C3
(7) Now, this solution is necessarily smaller than x,y,z since:
(A3)(B3)(C3) = (2a)(a - 3b)(a + 3b) = 2p
And from our previous work, either:
x3 = (2p)*(p2 + 3q2) or
z3 = (2p)*(p2 + 3q2)
QED
Wednesday, May 25, 2005
Fermat's Last Theorem: n = 3: Step 2
Today, I will show the proof for this lemma:
Lemma: if p,q are coprime, p,q opposite parity, then gcd(2p,p2 + 3q2) = 1 or 3
(1) Assume that there is a prime f which divides both 2p and p2 + 3q2.
(2) We know that it can't be 2 since p2 + 3q2 is odd since p,q have opposite parity.
(3) Let's assume that f is greater than 3. So that there exist P,Q such that:
2p = fP, p2 + 3q2 = Qf
(4) Now, f isn't 2 so we know that 2 must divide P so there exists a value H that is half of P and:
p = fH
(5) So combining the two equations, we get:
3q2 = Qf - p2 = Qf - f2H2 = f(Q - fH2)
(6) f doesn't divide 3 since it is greater than 3. So by Euclid's Lemma, it must divide q.
(7) But this contradicts p,q being coprime since it also divides p so we reject our assumption.
QED
Tuesday, May 24, 2005
Fermat's Last Theorem: n = 3: Step 1
The first step will be stated as a lemma:
Lemma: x3 + y3 = z3 has a solution only if there exists p,q such that:
(a) gcd(p,q)=1
(b) p,q are positive
(c) p,q have opposite parity (that is, one is even, one is odd)
(d) 2p*(p2 + 3q2) is a cube.
(1) We can assume that x,y,z are coprime.
(2) Since, x,y,z are coprime, we know that at most one of them is even.
(3) We also know that at least one of them is even since if x and y are odd, then z must be even.
(4) So, we now divide this proof up into Case I: z is even and Case II: x is even. Since x,y are symmetrical, Case II will also cover the case where y is even.
Case I: z is even
(1) Then x,y are odd.
(2) x + y and x - y are even.
(3) Let 2p = x + y and 2q = x - y
(4) Then:
x = (1/2)[x + y + ( x - y )] = p + q
y = (1/2)[x + y - ( x - y )] = p - q
(5) Now gcd(p,q) = 1
(a) Assume f = gcd(p,q) is greater than 1
(b) Then there exists P,Q such that p = fP, q = fQ
(c) But then f divides both x,y since x = f(P + Q), y = f(P - Q)
(d) This is a contradiction since x,y are coprime.
(6) We can assume that p,q are positive
(a) From before p = (1/2)(x + y), q = (1/2)(x - y)
(b) x cannot equal y since they are coprime.
(c) if x + y is negative, then substitute (-x),(-y) since x3 + y3 = z3 implies that (-x)3 + (-y)3 = (-z)3
(d) if y is greater than x then flip x,y since they are symmetric.
(e) This covers all cases.
(7) p,q have to have different parities since x,y are both odd.
(8) Finally, 2p*(p2 + 3q2) is a cube.
z3 = x3 + y3 =
= (x + y)(x2 - xy + y2) =
= (p + q + p - q)[(p+q)2 - (p+q)(p-q) + (p-q)2] =
= 2p(p2 + 3q2)
Case II: x is even
(1) Then z,y are odd since they are coprime to x.
(2) z+y, z-y are both even.
(3) There exists p,q such that 2p = (z - y), 2q = (z + y)
(4) And z = (1/2)[(z - y) + (z + y)] = (1/2)(2p + 2q) = p + q, y = (1/2)[(z + y) - (z - y)] = (1/2)(2q - 2p) = q-p
(5) p,q have opposite parity since z,y are odd.
(6) gcd(p,q)= 1 [Same argument as Case I]
(7) p,q are positive [Same argument as Case I]
(8) 2p*(p2 + 3q2) is a cube.
x3 = z3 - y3 =
= (z - y)(z2 + zy + y2) =
= [q + p - (q - p)][(q+p)2 + (q+p)(q-p) + (q-p)2] =
= 2p*(p2 + 3q2)
QED
Sunday, May 22, 2005
Fermat's Last Theorem: Proof for n=3
One proof involved a very innovative method using irrational numbers. Unfortunately, Euler made a mistake in his proof. Despite this, his method revealed a very promising approach to Fermat's Last Theorem which was later taken up by Gauss, Dirichlet , and Kummer. I discuss the details of this method and Euler's mistake in another blog.
The other proof is less generalizable but still brilliant. This is the proof that I will present in today's blog.
The details of this proof are based largely on the work by H. M. Edwards in his book: Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory.
Theorem: Euler's Proof for FLT: n = 3
x3 + y3 = z3 has integer solutions -> xyz = 0
(1) Let's assume that we have solutions x,y,z to the above equation.
(2) We can assume that x,y,z are coprime. [See here for the proof]
(3) First, we observe that there must exist p,q such that (see here for proof):
(a) gcd(p,q)=1
(b) p,q have opposite parities (one is odd; one is even)
(c) p,q are positive.
(d) 2p*(p2 + 3q2) is a cube.
(4) Second, we know that gcd(2p,p2+3q2) is either 1 or 3. (see here for proof).
(5) If gcd(2p,p2+3q2)=1, then there must be a smaller solution to Fermat's Last Theorem n=3. (see here for proof).
(6) Likewise, if gcd(2p,p2+3q2)=3, then there must be a smaller solution to Fermat's Last Theorem n=3. (see here for proof).
(7) But then there is necessarily a smaller solution and we could use the same argument on this smaller solution to show the existence of an even smaller solution. We have thus shown a condition of infinite descent.
QED
