i - 1 and Fermat's Last Theorem n = 4

Today's blog continues a proof that was first presented in a previous blog. If you are new to unique factorization, start here. If you are new to Gaussian Integers, start here. To begin this proof, start here.

Today's result is based on work presented by Paulo Ribenboim's Fermat's Last Theorem for Amateurs.

Today's blog applies the Gaussian prime λ to Fermat's Last Theorem n = 4. As before, I use Greek letters to refer to Gaussian Integers and Latin letters to refer to rational integers. I introduced the Gaussian Prime λ in a previous blog.

Lemma: if α⁴ + β⁴ = γ² where gcd(α,β,γ)=1, then we can assume that λ divides α * β

(1) Assume λ does not divide α * β

(2) Then, from a previous lemma, we know that α⁴ ≡ 1 (mod λ⁶), β⁴ ≡ 1 (mod λ⁶)

(3) Then, there exists δ₁, δ₂ where: [based on the definition of ≡ found here]
α⁴ - 1 = λ⁶ * δ₁.
β⁴ - 1 = λ⁶ * δ₂

(4) So that:
α⁴ = λ⁶*δ₁ + 1.
β⁴ = λ⁶*δ₂ + 1.

(5) Then:
γ² = λ⁶*δ₁ + 1 + λ⁶*δ₂ + 1 = λ⁶(δ₁ + δ₂) + 2.

(6) Since 2 = i*λ², we get: [From a lemma, found here]
γ² = λ⁶(δ₁ + δ₂) + i*λ² =λ²[λ⁴(δ₁ + δ₂) + i]

(7) Which shows that:
λ² divides γ²

(8) And from this, that:
λ divides γ [Since we have a Gaussian Integer proofs for gcd, unique factorization, and Euclid's Lemma, we can use the proof here. ]

(10) This means that λ⁴ does not divide γ².

(a) Assume that λ⁴ does divide γ².
(b) Then λ⁴ would divide 2 since γ² = λ⁴(λ²δ₁ + λ²δ₂) + 2. [Since d divides a + b and d divides a, implies d divides b]
(c) Then there exists ζ such that 2 = λ⁴ * ζ
(d) Since 2 = i *λ², we get:
i *λ²= λ⁴*ζ
(e) Dividing both sides from λ² gives:
i = λ²*ζ = (1-i)²*ζ = -2i * ζ
(f) Which is impossible since ζ is a Gaussian Integer and not a fraction.

(11) This also gives us that λ² does not divide γ [if it did, then λ⁴ would divide γ² which it cannot.]

(12) Now, since λ divides γ, there must exist a value η such that γ = λ * η

(13) We know that λ cannot divide η. [If it did, then λ² would divide γ]

(14) Now, we have our contradiction. Here are the details

(15) In step(5), we showed that:
γ² = λ⁶*δ₁ + 1 + λ⁶*δ₂ + 1 = λ⁶(δ₁ + δ₂) + 2.

(16) Letting μ = δ₁ + δ₂ and letting γ = λ * η, we get:
(λ*η)² = λ²*η² = λ⁶ * μ + i*(λ²)

(17) Dividing both sides by λ², we get:
η² = λ⁴ * μ + i.

(18) Squaring both sides gives us:
η⁴ = (λ⁴ * μ + i)² = λ⁸*μ² + 2*λ⁴*μ*i -1 =
λ⁸*μ² + ( i*λ²)*λ⁴*μ*i -1 =
λ⁶[λ²*μ² -μ] - 1

(19) So, that we get:
η⁴ ≡ -1 (mod λ⁶)

(20) But, since λ does not divide η, from a previous lemma, we get:
η⁴ ≡ 1 (mod λ ⁶)

(21) It is impossible for both of these modulo λ⁶ values to be true.

(a) Assume η⁴ ≡ -1 (mod λ⁶) and η⁴ ≡ 1 (mod λ⁶).
(b) λ⁶ divides both η⁴ - 1 and η⁴ + 1.
(c) Then there exists ν₁ and ν₂ such that;
η - 1 = λ⁶ * ν₁
η + 1 = λ⁶ * ν₂
(d) Adding the two equations together gives us:
2*η = λ⁶[ν₁ + ν₂]=
i*(λ²)*η = λ⁶[ν₁ + ν₂]
(e) Dividing both sides by λ² gives us:
i*η = λ⁴[ν₁ + ν₂]
(f) But this then implies that λ divides η which goes against assumption. [Note, it doesn't divide i because it is not a unit. It therefore divides η by Euclid's Lemma for Gaussian Integers]

QED

Gaussian Integers: properties of 1 - i

Today's blog continues a proof that was first presented in a previous blog. If you are new to unique factorization, start here. If you are new to Gaussian Integers, start here. To begin this proof, start here.

Today's result is based on work presented by Paulo Ribenboim's Fermat's Last Theorem for Amateurs.

Today's blog focuses on properties of the Gaussian prime λ which we will need to prove Fermat's Last Theorem for n = 4.

Definion 1: λ is a Gaussian Integer that is equal to 1 - i.

Lemma 1: λ is a prime.

Since Norm(λ) = (1 - i)(1 + i) = 1 + 1 = 2. [See here for further details on why this proves that λ is a prime.]

QED

Lemma 2: λ divides 2

i * λ² = (i)(1 - i)² = (i)(1 -2i - 1) = 2.

QED

Corollary 2.1: λ⁶ divides 8

From Lemma 2 above,
(i*λ²)³ =(-i)*λ⁶= 8

QED

Lemma 3: λ*i = (1 + i)

λ * i = i(1 - i) = i + 1

QED

Definition 2: ≡ is relation such that α ≡ β (mod γ) means that α - β is divisible by γ.

We describe this relationship by saying that α modulus γ is equal to β

This definition is true for Gaussian Integers or standard integers. For example, we know that 6 ≡ 2 (mod 4) since 4 divides 6 - 2. We then can say that 6 modulus 4 is equal to 2.

Lemma 4: Let α be any Gaussian Integer. α modulus 2 equals 0, 1, i, or λ

(1) For any α, there exists a,b such that α = a + bi. [Definition of Gaussian Integer]

Case I: a is even, b is even

In this case, α ≡ 0 (mod 2) since a is even, b is even implies there exists A, B such that a = 2A, b = 2B and α = 2A + 2Bi = 2(A+Bi)

Case II: a is odd, b is even

In this case, α ≡ 1 (mod 2) since there exists A, B such that a = 2A+1, b = 2B and α - 1 = 2A + 1 - 1 + 2Bi = 2(A + Bi)

Case III: a is even, b is odd

In this case, α ≡ i (mod 2) since there exists A, B such that a = 2A, b = 2B + 1 and α - i = 2A + (2B+1)i - i = 2A + 2Bi = 2(A+Bi)

Case IV: a is odd, b is odd

In this case, α ≡ λ (mod 2) since there exists A,B such that a = 2A + 1, b = 2B + 1, and α - λ = 2A + 1 + (2B + 1)i - (1 - i) = 2A + 1 + 2Bi + i + i - 1 = 2A + 2B + 2i = 2(A + B + i)

QED

Lemma 5: if α is a Gaussian Integer that is not divisible by λ, then α⁴ ≡ 1 (mod λ⁶).

(1) Since α is not divisible by λ, it cannot be divisible by 2. [See Lemma 2 above]

(2) We also know that modulo 2, it cannot be λ. If α modulo 2 is λ then it would imply that α is divisible by λ which it is not.

(3) So, we are left with α ≡ 1 or i (mod 2) from Lemma 4.

(4) α⁴ ≡ 1 (mod 8) since:

Case I: α ≡ 1 (mod 2)

(a) (α + 1) ≡ (α - 1) ≡ 0 (mod 2)

(b) (α² - 1) ≡ (α + 1)(α - 1) ≡ 0 (mod 4)

(c) (α² + 1) ≡ 0 (mod 2)

(d) (α⁴ - 1) ≡ (α² + 1)(α² - 1) ≡ 0 (mod 8)

Case II: α ≡ i (mod 2)

(a) (α + i) ≡ (α - i) ≡ 0 (mod 2)

(b) (α² + 1) ≡ (α + i)(α - i) ≡ 0 (mod 4)

(c) (α² - 1) ≡ 0 (mod 2)

(d) (α⁴ - 1) ≡ (α² + 1)(α² - 1) ≡ 0 (mod 8)

(5) And this proves that α⁴ ≡ 1 (mod λ⁶) using Corollary 2.1 above.

QED

Proof for n=4 using Gaussian Integers

In today's blog, I will show how it is possible to use Gaussian Integers to establish a proof for Fermat's Last Theorem n = 4. Previously, I showed two proofs for this result. I showed a standard proof based on Pythagorean Triples (see here). Also, I showed how it could be derived from Fermat's proof that a right triangle cannot have a square area (see here).

The proof for the case n = 4 using Gaussian Integer is both very strange and very interesting. The proof that I present is taken from Paul Ribenboem's book Fermat's Last Theorem for Amateurs.

Please note that I use Greek letters to represent Gaussian Integers and Latin letters to represent rational integers. This is really to emphasize that reasoning with Gaussian Integers requires different assumptions. For example, the Well Ordering Principle no longer applies and 2 is no longer a prime.

Theorem: x⁴ + y⁴ = z² has no solution in Gaussian Integers where xyz ≠ 0.

(1) First, I will show that if there is a solution in rational integers, then the following is true:

There exists α, β, γ, ε, λ such that:
ε * λ⁴ⁿ * α⁴ + β⁴ = γ² where n ≥ 2. [See here for proof.]

(2) Second, I will show that if (1) is true, then there is another set of values: ε₁, α₁, β₁, γ₁ such that:

ε₁ * λ^4(n-1) * α₁⁴ + β₁⁴ = γ₁². [See here for proof.]

(3) But then, repeating step (2) again and again, we eventually get to values: α_i, β_i, ε_i, γ_i where

ε_i * λ⁴*α_i⁴ + β_i⁴ = γ_i²

(4) Which contradicts step (1) where n ≥ 2. So we reject that there is a solution to FLT for n=4.

QED

Bezout's Identity for Gaussian Integers

Today's blog continues my discussion of Gaussian Integers. If you are unfamiliar with the concept of unique factorization, start here. For the full discussion about Gaussian Integers, start here.

Bezout's Identity states that the greatest common denominator of any two integers can be expressed as a linear combination with two other integers. For example, because we know that gcd(2,3)=1, we also know that 1 = 2(-1) + 3(1). The proof for rational integers can be found here.

Bezout's Identity is one of three main ideas that are required in order to prove unique factorization. The other two ideas you need are a Division Algorithm, which I detailed in my last blog, and Euclid's Lemma, which I will discuss in a future blog.

Before discussing Bezout's Identity, we will need a lemma that shows that the notion of greatest common denominator applies to Gaussian Integers.

Using the Division Algorithm for Gaussian Integers and Euclid's method for greatest common denominators, we are set. The idea behind Euclid's Method is to do a continuous number of divisions.

Let's assume that we have a,b. First, we divide a by b and get a remainder which I will call r₁. Then we divide b by r₁ and we get a second remainder which I will call r₂. We can keep repeating this until eventually we get a remainder which is 0. We know that this will happen because each remainder is guaranteed by the Division Algorithm to be smaller than the remainder before. After at most b iterations, we will reach a remainder of 0.

Euclid's Method tells us that the last r_i value we use is the remainder. It is guaranteed to be at least 1. To make the idea behind this lemma as clear as possible, I will throw out one very simple lemma:

Lemma 1: d divides a, d divides b , a = b + c, then d divides c.

(1) d divides a → there exists A such that a = dA.
(2) d divides b → there exists B such that b = dB
(3) a = b + c → c = a - b = d(A - B)

QED

Lemma 2: For any two Gaussian Integers, it is possible to find the greatest common denominator.

(1) Let α, β be two Gaussian Integers.

(2) We know that there exists η₁,δ₁ such that:
α = η₁β + δ₁ and 0 ≤ δ₁ which is less than β

(3) β = η_2*δ₁ + δ₂

(4) And: δ₁ = η_3*δ₂ + δ₃

(5) We can keep repeating this until eventually we get:
δ_n-3 = η_n-1 * δ_n-2 + δ_n-1
δ_n-2 = η_n * δ_n-1 + δ_n
δ_n-1 = η_n+1* δ_n

(6) We know that we eventually get to this point since Norm(δ_i+1) is always less than the Norm(δ_i) by the Division Algorithm.

(7) Now, we know that δ_n divides δ_n-1 by Step #5. We also know that δ_n divides δ_n-2 and therefore, it also divides δ_n-3 and so on up to β and then α. In other words, it is a common divisor for α and β. [By Lemma 1]

(8) But we also know that if a certain value γ divides both α and β, then it will necessarily divide δ₁ and that it will also necessarily divide δ₂ and so on. [Again, by Lemma 1]

(9) In other words, we have proven that δ_n is the greatest common divisor.

QED

Corollary: All quadratic integers that are characterized by a Division Algorithm possess a greatest common denominator.

This is true since all the arguments above only assume a Division Algorithm.

QED

Here is the proof for Bezout's Identity:

Lemma 3: Let α, β be Gaussian Integers. Then there exist two other Gaussian Integers, let's say, ζ, η such that gcd(α,β) = ζα + ηβ

(1) Based on Lemma 2, we have the following:
δ_n-2 = η_n * δ_n-1 + δ_n

(2) This can be restated as:
δ_n = δ_n-2 - η_n * δ_n-1

(3) Now, if we let ζ = 1 and γ = -η we have:
δ_n = ζ * (δ_n-2) + γ * (δ_n-1)

(4) Let's define the following:
δ₀ = β
δ_-1 = α

With this definition, we can view each step as a continuum of different δ_i values all the way up.

(5) Now, if you look at equation (2), it shows that at each point, any δ_i can be restated in terms of smaller values of δ_i-1 and δ_i-2. So that:
δ_n = δ_n-2 - η_n * δ_n-1 =
δ_n-2 - η_n * (δ_n-3 - η_n-1 * δ_n-2) =
δ_n-2(1 + η_n*η_n-1) + δ_n-3(-η_n)

(6) Setting ζ = 1 + η_n * η_n-1, γ = -η_n, we get:
δ_n = ζ * δ_n-2 + γ*δ_n-3

(7) Again, we can take (5) and move it up one using the same equation:
δ_n = ζ * (δ_n-4 - η_n-2 * δ_n-3) + γ * δ_n-3 =
= δ_n-3(-ζ *η_n-2 + γ) + δ_n-4(ζ)

(8) This shows that we can simplify the equation to a 1 smaller number which can be restated as a linear combination.

(9) Eventually, we get to:
δ_n = ζ * α + η * β

where ζ = some Gaussian Integer value and η = some Gaussian Integer value.

QED

But now, with the proof of Bezout's Identity, we can get Euclid's Lemma as a corollary.

Corollary 3.1: Euclid's Lemma: if π is a prime that divides α * β, then it divides α or it divides β


(1) Assume π doesn't divide α.

Please note: π is selected as the Greek character equivalent of p. I am not using π to represent 3.14....

(2) Then gcd(π,α) = 1. [By definition of gcd, #1]

(3) From Lemma 3, we know that there exists ζ, η such that:
1 = ζ * α + η * π.

(4) Multiplying both sides by β gives us:
β = ζ * α * β + η * π * β

(5) Since π divides α * β, we know that there exists γ such that:
α * β = π * γ

(6) So we have:
β = ζ * π * γ + η * π * β = π * (ζ * γ + η * β)

QED

Corollary 3.2: Euclid's Generalized Lemma: if π divides α₁ * α₂ * ... * α_n, then π divides at least one of the elements in the product.


(1) Let β₁ = α₂ * ... * α_n

(2) Then π divides α₁ * β₁ which means by Euclid's Lemma that π divides α₁ or β₁.

(3) If it divides α₁, we are done.

(4) If it divides β₁, then we set β₂ = α₃ * ... * α_n and repeat the argument.

(5) Eventually, we hit some α_i that is divisible by π.

QED

Corollary 3.3 These results apply to all quadratic integers characterized by a Division Algorithm

Again, none of these arguments are specific to Gaussian Integers. They are true of any quadratic integer that has a division algorithm.

QED

Division Algorithm for Gaussian Integers

In my previous blog, I showed the details for a proof that Gaussian Integers have unique factorization. If any of the information that I present gets confusing, I suggest that readers start here where I explain about unique factorization, Gaussian Integers, the norm function, and the reason I am using Greek letters to represent Gaussian Integers.

In today's blog, I will show how using the norm function, it is possible to arrive at a Division Algorithm for Gaussian Integers.

The Division Algorithm for rational integers is based on the Well-Ordering Principle and can be found here. It states that whenever we divide one integer by another integer, we are left with a quotient and remainder that are both integers and which are both unique to the division and the remainder is guaranteed to be less than the divisor.

In the lemma below I used Greek letters for Gaussian Integers, Latin letters for rational integers, and Z[i] to represent the set of Gaussian Integers.

Lemma: Division Algorithm for Gaussian Integers

Given: α, γ ∈ Z[i]

Then: there exists ζ, δ such that: α = ζγ + δ and Norm(δ) is less than Norm(γ)

(1) There exists a,b,c,d such that:
α = a + bi
γ = c + di

(2) α / γ = (a + bi) / (c + di) = (a + bi)(c - di) / (c² + d²) =
= (ac - adi + bci - bdi²)/(c² + d²) =
=(ac + bd)/(c² + d²) + i[(bc - ad)/(c² + d²)]

(3) Let r = (ac + bd)/(c² + d²).

(4) Let s = (bc - ad)/(c² + d²)

(5) So, α / γ = r + si

(6) And we know that both r,s are rational. We do not know if they are integers.

(7) We know that there are m,n which are integers such that absolute(r - m) ≤ (1/2) and absolute(s - n) ≤ (1/2). [For proof of this see here]

(8) Let ζ = m + ni.

(9) Let δ = α - ζγ → α = ζγ + δ

(10) Norm(δ) = Norm(α - ζγ) =
= Norm(γ[(α/γ) - ζ] = Norm(α/γ - ζ) * Norm(γ) =
= Norm(r + si - [m + ni]) * Norm(γ) =
= Norm(r - m + si - ni) * Norm(γ) =
= Norm([r - m] + [s -n]i) * Norm(γ) =
= [(r - m)² + (s - n)²] * Norm(γ) ≤ [ (1/2)² + (1/2)²]*Norm(γ) =
= (1/2)*Norm(γ) which is less than Norm(γ)

QED

Properties of Gaussian Integers

In my last blog, I spoke about relationship between Gaussian Integers and Fermat's Last Theorem. I went into some detail about norm function which provides a mapping from Gaussian Integers to standard integers. Anyone who is not familiar with Gaussian Integers or the norm function should start here. Anyone not familiar with the idea of unique factorization, should start here.

When we look at standard integers, officially called rational integers, we recognize that most of their properties are based on the Well Ordering Principle. This is the idea that for any given set of nonnegative integers, there is always one that is the smallest. If any one is interested in seeing the proofs related to the Well Ordering Principle and rational integers, you can check out here.

With Gaussian Integers, we are looking at a domain where the Well Ordering Principle does not apply. In the case of rational integers, it was clear that they can be thought to extend across a number line. Gaussian Integers, in contrast, extend across two number lines: a rational integer line and an i integer line.

For this reason, the previous proofs do not apply. We will need to come up with new proofs for the basic ideas. The basic idea of unique factorization is built from the following ideas:

(1) A Division Algorithm: What assumptions can we make about division? What assumptions can we make about quotients and remainders? See here for the algorithm with regard to rational integers. See here for the algorithm with regard to Gaussian Integers.

(2) Bezout's Identity: This is the idea that the greatest common denominator of any two integers can be represented as an equation based on two other integers. See here for the identity with regard to rational integers. See here for the proof of the identity with regard to Gaussian Integers.

(3) Euclid's Lemma: This is the idea that if a prime integer divides the product of two integers, then either it divides the first integer or it divides the second. See here for the proof of Euclid's Lemma regarding rational integers. See here for the proof with regard to Gaussian Integers.

Unique Factorization, it turns out, comes directly from Euclid's Lemma. As a convention, I will use Greek letters to represent Gaussian Integers and Latin letters to represent Rational Integers. So that: α = a + bi where α is a Gaussian Integer and a,b are rational integers.

There is one trick that we need to do in addition to using norms. We need to talk about the idea of associates.

Definition: Associates: Two numbers are associates if one is equal to the other multiplied by a unit.

The Gaussian Integers have four different units: i,-i,1,-1 (see Corollary 4.1, here). So, we can see that 4, -4, 4i, and -4i are all associates of each other. So, when we are talking about unique factorization of primes, we are considering prime associates to be the same prime. So, when we prove unique factorization, we are really proving a unique set of prime-associates.

Theorem: Gaussian Integers posess Unique Factorization.

(1) We know that all non-zero, non-units are either primes or composed of primes. [By the definition of primes]
(2) Let's assume that a given number is made of two different sets of primes.
(4) So α = β₁*β₂*...*β_r = γ₁*γ₂*...*γ_s
(5) Now each prime β_i must necessarily match a prime in γ_j by Euclid's Generalized Lemma. [See here for the proof of Euclid's Generalized Lemma for Gaussian Integers]
(6) But we can make the same argument for all β_i so there must be an equal prime or associate in the set of γ_j.
(7) But then, there cannot be any prime left over since if we divide all the β_i, then we are left with a unit.
(8) So, we have proven that the set of primes is necessarily unique.

QED

Corollary: All Euclidean Integers posessess unique factorization.

(1) By definition, all Euclidean Integers are characterized by a Division Algorithm. [See here for review of Euclidean Integers]

(2) All Euclidean Integers are therefore also characterized by Euclid's Generalized Lemma. [See here for the proof.]

(3) With these two results, the same arguments above apply to all Euclidean Integers.

QED

Norms for Gaussian Integers

In my last blog, I spoke about the importance of unique factorization of integers. This is the idea that all integers can be broken up into a unique set of prime numbers. In today's blog, I will go over some basic lemmas regarding norms. I introduced norms and conjugates in a previous blog.

Carl Friedrich Gauss and Leonhard Euler both proposed extensions of integers that used irrational numbers that they were able to use to make elegant proofs for Fermat's Last Theorem.

A set of integers is extended by including additional values. In standard integers, the values are positive and negative whole numbers and 0. In extended integers, we can include additional values such as i, 5i, etc. Gaussian integers include all of the standard integers plus the addition of multiples of i. In other words, a Gaussian Integer is defined by two integers: a,b where each Gaussian integer can be represented a + bi.

In my previous blog, I spoke about using a special function, the norm, to reason about Gaussian Integers. I will now present a few interesting lemma. To distinguish between Gaussian Integers and standard integers, I will use Greek letters to represent Gaussian Integers and Latin letters to represent standard integers:

Lemma 1: Norm(α) = 0 if and only if α = 0

(1) Norm(α) = Norm(a + bi) = (a + bi)(a - bi) = a² + b²
(2) But if a ≠ 0, then a² + b² > 0.
(3) And the same holds true if b ≠ 0.

QED

In mathematical notation, the conjugate of a Gaussian Integer is represented with an overline over it. So, if α is a Gaussian Integer, then: α is the conjugate. This is important since the norm is equal to a Gaussian Integer multiplied by its conjugate.

Lemma 2: (α * β) = α * β

(1) (α * β) = (a + bi) * (c + di) = (ac - bd) + i(ad + bc)
(2) So, α * β = (ac - bd) - i(ad + bc)
(3) And, α * β = (a - bi) * (c - di) = (ac - bd) - i(ad + bc).
QED

Lemma 3: Norm(α*β) = Norm(α) * Norm(β)

(1) Norm(α*β) = (α*β)(α*β) =
(2) = α*β*α*β [ From Lemma 2 ]
(3) = (α*α)(β*β)
(4) =Norm(α)*Norm(β)

QED

In standard integers, we speak about 1, -1 as being units -- that is, numbers which divide all other numbers. This is important because when we are discussing prime numbers or relatively prime numbers, we are necessarily talking about numbers other than 0 or the units.

In the realm of Gaussian Integers, a unit is defined as any number that divides 1.

Lemma 4: if α is a unit, then Norm(α) = ±1

Proof:

(1) If α is a unit, then there exists another value β such that α * β = 1.
(2) Now, Norm(α * β) = Norm(1) = 1 = Norm(α) * Norm(β)
(3) But if either Norm(α) ≠ ±1 or Norm(β) ≠ ± 1, then the Norm(α * β) couldn't equal 1 (since there are no other rational integers that multiply to 1).
(4) So, Norm(α) must equal ± 1.

QED

Corollary 4.1: The only units for Gaussian Integers are i,-i,1,-1

Proof:

(1) N(i) = i*(-i) = 1 [See Definition 2 here for details if needed]

(2) N(-i) = (-i)*i = 1 [See Definition 2 here for details if needed]

(3) N(1) = 1*1 = 1 [See Definition 2 here for details if needed]

(4) N(-1) = (-1)*(-1) = 1 [See Definition 2 here for details if needed]

(5) If N(α) is a unit where α = a + bi, then:]

(a + bi)(a - bi) = a² + b² = 1

(6) But this can only occur if a=0 or b=0 since:

(a) if a ≠ 0 and b≠ 0

(b) Then abs(a) ≥ 1 and abs(b) ≥ 1

(c) And, a² + b² ≥ 2

(7) But then the only possible units are 1, -1, i, -i

(a) if a = 0, then b = ± 1 so that we have α = i or α = -i

(b) if b=0, then a = ± 1 so that we have α=1 or α=-1

QED

We are now ready to define a Gaussian Prime. A Gaussian prime is any Gaussian Integer which is not 0 or a unit which is only divisible by a itself or a unit.

Lemma 5: if Norm(α) is a standard prime, then α is a prime.

(1) So, we start with Norm(α) = p which is a standard prime.
(2) Assume α is not a prime.
(3) Then there exists two Gaussian Integers: β, γ that are not units such that: α = β * γ.
(4) And then Norm(β * γ) = Norm(β) * Norm(γ) [By Lemma 3 above]
(5) Since Norm is a mapping function to standard integers, we know that there exists b,g such that:
b = Norm(β)
g = Norm(γ)
(6) We know that Norm(β * γ) = p and we know that b,q ≠ 1 [By Lemma 4, since they are not units]
(7) But then p = b * g which is impossible since p is a prime.
(8) Therefore, we reject our assumption in (2).

QED

Lemma 6: (α/β) = α / β

(1) There exists a,b,c,d such that α = a + bi. β = c + di.

(2) (α/β) =








[From Lemma 2 above]









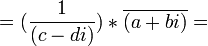
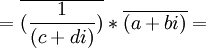
= (a + bi) / (c + di)

QED

Lemma 7: Norm(α / β) = Norm(α) / Norm(β)

(1) Norm(α / β) = (α / β) * (α / β) [Definition of Norm]

= (α / β) * α / β = Norm(α) / Norm (β)

QED

Corollary 7.1: If α divides β, then Norm(α) divides Norm(β)

Proof:

(1) Assume that α divides β.

(2) Then there exists an integer γ such that γ = β / α.

(3) By the definition of a norm (see here), Norm(γ) is a rational integer.

(4) But then Norm(β)/Norm(α) = Norm(γ) which means that Norm(α) must divide Norm(β).

QED

In my next blog, I will prove that Gaussian Integers possess unique factorization.

The lemmas from today's blog were taken from an excellent book by Harold M. Stark called An Introduction to Number Theory .

Unique Factorization

Carl Friedrich Gauss was the first mathematician to understand the importance of unique factorization in relation to algebraic integers. While unique factorization was a known property of integers since the time of Euclid, it is not true that it is necessarily a property of all algebraic integers.

Unique factorization is the idea that a given whole number consists of a unique set of primes. For every set of unique primes, there is one and only one number that can be built. For every number, there is one and only one unique set of primes.

Before Gauss, this idea was probably not interesting to mathematicians because it is so clearly true in the case of integers. On the other hand, when Leonhard Euler presented his proof for Fermat's Last Theorem n=3, he introduced a new set of integers in the form of a + b√-3. This was a brilliant proof and yet he made a mistake. He assumed that unique factorization automatically applied. It was Gauss's insight that this assumption requires proof.

Gauss took the idea of unique factorization very seriously when he proposed what are today called Gaussian Integers. Using i-notation, where i is the square root of -1, a Gaussian integer is defined by the set of all values that can be created by a + bi where a,b are integers. It is also represented by the form Z[i]. Using this notation, Euler's proof used integers of the form Z[√-3].

The interesting idea behind Gaussian Integers is that any theorem which is true of all Gaussian Integers is also true of all integers since integers are Gaussian Integers wheren b = 0.

But how does one reason with Gaussian Integers? On the surface, it doesn't look like they will be offer any insights beyond the standard integers. In fact, it seems, on the surface, that reasoning about them will be more difficult since they themselves are more complicated. Using standard integers, we know that 5 is a prime. But in the realm of Gaussian Integers, it is not a prime since
5 = (2 + i)(2 - i) = 4 + 1 = 5.

Gaussian Integers are interesting because they allow us to factor equations in interesting ways. For example, the equation x⁴ + y⁴ can now be factored into (x² - y²i)(x² + y²i). Without Gaussian Integers, there wouldn't be an easy factoring. This was really Euler's motivation for extending the integers since he was able to break x³ + y³ into a form such as:
(x + y)(x + ay)(x + by).

Coming up with proofs about Gaussian integers becomes interesting with the introduction of a special function called the norm. The norm is a mapping function that maps any Gaussian Integer to a standard integer. The norm is important because it enables to us to define Gaussian primes and because it then enables us to establish unique factorization for Gaussian Integers.

How does one find a mapping function that is guaranteed to convert any Gaussian Integer to a standard integer? The answer comes from the following mathematical equation:

(a + b)(a - b) = aa -ab +ab - bb = a² - b²

In the case of i, this becomes:

(a + bi)(a - bi) = a² - (b²)(-1) = a² + b².

The form a - bi is called the conjugate of the Gaussian Integer. Hardy and Wright (see reference below) define the norm as the product of a Gaussian Integer with its conjugate. For purposes of my discussion on Gaussian integers, I will use the Hardy and Wright definition (I should point out that this is not the standard definition of norm, see here; I will revisit this point at a later time). The important point behind the norm is that it is a mapping between the Gaussian integers and the rational integers that allows us to reason about the Gaussian integers (see here for an example of using the norm for Gaussian integers to establish a division algorithm for Gaussian integers.)

For example, the norm of 5i is (0 + 5i)(0 - 5i) = 25. Interestingly, the norm of -5i is also 25. This is important because it shows that the norm is not a one-to-one mapping. All Gaussian integers and their conjugates share the same norm.

In summary, I offer the following definitions for Gaussian Integers:

Definition 1: Conjugate of a Gaussian Integer

The conjugate of a Gaussian Integer a+bi is a-bi and likewise, the conjugate of a Gaussian Integer a-bi is a+bi.

Definition 2: Norm of a Gaussian Integer: N(α) = α * α

Following Hardy and Write (see article by Eric Weisstein for details), the norm of a Gaussian integer α is α multiplied by its conjugate α, that is, the norm N(α) = α * α.

Over the next set of blogs, I will show how norms allow us to establish unique factorization for Gaussian Integers. My next blog will cover some basic ideas about Gaussian Integer norms.

References

• G. H. Hardy, E. M. Wright, Introduction to the Theory of Numbers, Oxford University Press, 1980
• Eric Weisstein, "Gaussian Integer", MathWorld,
  

Carl Friedrich Gauss

Carl Friedrich Gauss was born on April 17, 1777 to poor, working class parents in Brauschweig, Germany. His mother had been a maid and his father had been a laborer and handyman. His father, it is said, did not appreciate Gauss's abilities or his later accomplishments.

Gauss is considered to be one of the three greatest mathematicians of all time. The other two being Archimedes and Sir Isaac Newton. His accomplishments are so vast that this blog will only be a brief glimpse. For those interested in greater details, please check out the reference list at the end of this blog.

Gauss showed indications of mathematical genius very early. According to a popular story, he noticed a mistake in his father's calculations when he was only 3 years old. Later, he supposedly taught himself to read and by the time he was 8, he was already astounding people by his mathematical abilities. For example, there is a well known anecdote where a teacher gave his students an assignment to add up a series of 100 numbers. Instantly, Gauss said that he had completed the exercise (the story goes that he had figured that 100 numbers could be determined by the equation n(a+b)(1/2)=50(a+b) where n=100, a = the first digit in the sequence and b = the last digit in the sequence.)

Gauss's teachers would lend him books and try to help him along with his independent studies of the subject. In 1788, at the age of 11, he entered the Gymnasium, a college preparatory school. In 1792, at the age of 14, he received a stipend from the Duke of Brunswick which made him financially independent for the next 16 years and it was that year that he entered Brunswick College.

He entered the University at Gottigen in 1795 and became famous in 1796 at the age of 19 with his discovery on March 30 of a method for constructing a heptadecagon (a regular 17-sided polygon) using only a compass and ruler. He was so excited by this that he requested that a heptadecagon be placed on his tombstone. For his doctoral thesis, he proved the fundamental theorem of algebra which states that all polynomials of degree n have n different solutions in the domain of complex numbers.

Gauss's other discoveries include the law of quadratic reciprocity, Gaussian distribution, modular arithmetic, non-Euclidean geometry, the prime number theorem, the systematization of number theory, and the method of least squares. Gauss worked on many of these discoveries completely on his own without any collaborators.

Gauss also had a strong interest in astronomy. In 1801, the planetoid Ceres was first sighted. Gauss studied data abouts its orbit and was able to predict a second possible sighting which was confirmed on December 31, 1801. In 1805, he became Director of the Observatory in Gottingen.

Despite his fame in mathematics, Gauss never became a mathematics professor and only attended one math conference. It was said that he strongly disliked teaching. When his good friend Farkas Bolyai told him that his son has come up with a non-Euclidean geometry, Gauss responded:

"To praise it would amount to praising myself. For the entire content of the work ... coincides almost exactly with my own meditations which have occupied my mind for the past thirty or thiry-five years."

Gauss's personal life was filled with tragedy. His first wife died in 1809 and a few years later, his first son died. It was said that throughout his life, he never overcame the sadness of this event. His second wife died in 1831 after a long illness. He never married after that. He died on February 23, 1855.

Gauss did not publish most of his discoveries. They were published after his death.

His face can be found on the German Deutche mark from 1989 until 2001:


References for this blog:

• Biography, Carl Friedrich Gauss, Wikipedia
• Biography, Carl Friedrich Gauss, Geocities.Com/Rainforest
• G. Waldo Dunnington, Carl Friedrich Gauss: Titan of Science
• Carl Gauss, Disquisitiones Arithmeticae

Euler's Mistake

For those who are not familiar with Fermat's Last Theorem, you may wish to start here.

In Leonhard Euler's original proof for Fermat's Last Theorem n=3, he made a mistake. For anyone interested in seeing the details of the proof, it is perhaps comforting to know that a genius like Euler was capable of getting the details wrong. The details of this blog are based on Harold M. Edwards's book, Fermat's Last Theorem.

The mistake came when Euler tried to prove the key lemma of his proof. In his published proof, Euler attempted to prove this lemma using imaginary numbers. Euler is credited with the invention of the notation for imaginary numbers and one of the most fascinating equations ever derived which is known as Euler's Identity:

e^iπ=-1

So, it is not too surprising that he would apply this method to Fermat's proof. It is also very interesting to note that a less innovative method can be constructed based on Euler's other work. This is what I did in the proof that I presented earlier.

Also interesting is the fact that this technique turns out to be a very important innovation which makes possible additional proofs for n=5, n=7, and Kummer's proof for regular primes.

Euler tries to prove the following lemma:

Lemma: Given that p² + 3q² is a cube, show that there exist a,b such that p = a³ - 9ab² and q = 3a²b - 3b³.

Here's Euler's idea. What if we presuppose that there exists numbers of the form:
a + b√-3

If we allow that these numbers exist, then we have the following equation:

p² + 3q² = (p + q√-3)(p - q√-3)

So far so good. Mathematicals in general will allow any extension of numbers as long as the extension is logically consistent. The rational numbers extend the integers. Real numbers extend the rational numbers and Complex numbers extend the real numbers.

Euler proceeds to show that the two complex numbers (p + q√-3, p - q√-3) are relatively prime to each other. His proof here also works. I will add the details for this proof later.

He then concludes that the two complex numbers must, therefore, be cubes based on the reasoning of the Relatively Prime Divisor Lemma. This is the mistake!

In modern notation, Euler assumed that Z[√-3] was characterized by unique factorization. This is not completely correct. In actual fact, Z[(-1 + √-3)/2] is characterized by unique factorization. I go into more detail on this subject in my blog about Euclidean integers. If you are not familiar with quadratic integers, start here.

This result would be greatly extended by Carl Friedrich Gauss.

Fermat's Last Theorem: n = 3 : last lemma needed for proof

It may surprising that we only need one more lemma to finish Euler's proof for Fermat's Last Theorem: n=3. This is an easy one. For those interested in seeing the entire proof for Fermat's Last Theorem: n = 3, start here.

Lemma: For all odd numbers, there exists a value n such that the number is equal to 4n ± 1 with n greater than 0.

(1) Let S = the set of all odd numbers representable by 4n + 1 or 4n - 1

(2) We know that 1 is an element of this set since 1 = 4(0) + 1

(3) We can then presuppose that there is some value v such that all odd numbers less than or equal to v are describeable by 4n + 1 or 4n - 1. We know that v is greater or equal to 1

(4) Now, we will prove that if v is of the form 4n + 1 or 4n - 1, then v + 2 is also of this form.

Case I: v is of the form 4n + 1

v + 2 = 4n + 1 + 2 = 4n + 3 = 4(n+1) - 1

Case II: v is of the form 4n - 1

v + 2 = 4n - 1 + 2= 4n + 1

(5) By the Principle of Mathematical Induction, we have proven this lemma.

QED

Fermat's Last Theorem: n = 3 : multiplication with a2 + 3b2

Today's blog is a bit shorter than the previous ones. It shows the relationship which was probably the original reason why Pierre de Fermat was interested in this equation.

This is part of the larger proof for Fermat's Last Theorem: n=3 which was first published by Leonhard Euler.

Lemma: Multiplying two polynomials of the form a² + 3b² results in a polynomial with the same form.

(a² + 3b²)(c² + 3d²) = a² (c² + 3d²) + 3b² (c² + 3d²) =
= a²c² + 3a²d² + 3b²c² +9b²d² =
= a²c² - 6abcd + 9b²d² + 3a²d² + 6abcd + 3b²c² =
= (ac - 3bd)² + 3(ad + bc)²

QED

Fermat's Last Theorem: n = 3: Division of a2 + 3b2 by 2

In today's blog, I will go over the case of where a² + 3b² is an even number. This result is part of the proof of Fermat's Last Theorem for n=3. If you would like to see the full proof, start here.

Lemma: if 2 divides a polynomial of form a² + 3b², then 4 also divides the polynomial and this division by 4 results in another polynomial of the same form.

In other words, we will prove two propositions:

• if 2 divides a² + 3b², then 4 also divides it.
• if 4 divides a² + 3b², then there exists c,d such that a² + 3b² = 4*(c² + 3d²)

(1) We know that a,b have the same parity (they are both odd or they are both even). Otherwise, a² + 3b² would not be divisible by 2

(2) If they are both even, then it is easy to show that 4 divides a² + 3b² and that the result is of the same form:

(a) There exists c,d such that a = 2c and b = 2d
(b) a² + 3b² = (2c)² + 3(2d)² = 4(c² + 3d²)

(3) So, we can assume that they are both odd.

(4) Now, there exists m,n such that a = 4m ± 1, b = 4n ± 1 [See here for proof]

(5) From this, we know that 4 divides either a + b or a - b

(6) I will now show that in both cases, the lemma is proven.

Case I: 4 divides a + b

(a) First, 4(a² + 3b²) = (1² + 3*1²)(a² + 3b²) = (a - 3b)² + 3(a + b)² [See here for proof]

(b) Since a - 3b = (a + b) - 4b, we know that 4 divides a - 3b

(c) So, this gives us that 4² divides (a - 3b)² + 3(a + b)² which also means that:
4 divides a² + 3b² [Since 4² divides (a - 3b)² + 3(a+b)² implies 4² divides 4(a² + 3b²)]

(d) Since 4 divides a - 3b and a + b, we know that there exists u,v such that: u = (a - 3b)/4 and v = (a + b)/4

(e) 4(u² + 3v²) = 4{[(1/4)(a - 3b)]² + 3[(1/4)(a + b)]²} =
= (1/4)(a² + 9b² + 3a² + 3b²) =
= (1/4)(4a² + 12b²) = a² + 3b²

Case II: 4 divides a - b

(a) The argument here is the same as for case I except that we set 4(a² + 3b²) = (1² + 3*(-1)²)(a² + 3b²) = (a + 3b)² + 3(a - b)² [See here for proof.]

(b) Then after proving that 4² divides this result, we let u = (1/4)(a + 3b) and let v = (1/4)(a - b).

(c) Then 4(u² + 3v²) = a² + 3b²

QED

Fermat's Last Theorem: n = 3 : Division with a2 + 3b2

In today's blog, I will show that if you divide a polyonomial of form a² + 3b² with a prime of this same form, then you end up a polynomial that still has the same form.

This result is needed for the proof of Fermat's Last Theorem for n=3 that was first presented by Leonhard Euler. For those interested in seeing the entire proof, please start here.

Lemma: if a prime of form p² + 3q² divides a² + 3b², then there exists c,d such that:
a² + 3b² = (p² + 3q²)(c² + 3d²)

(1) There exists f such that a² + 3b² = (p² + 3q²)f.

(2) (pb - aq)(pb + aq) = p²b² - a²q² + (3q²b² - 3q²b²) =
= p²b² + 3q²b² - 3q²b² - a²q² =
= b² ( p² + 3q² ) - q² ( a² + 3b² )

(3) Now the prime p² + 3q² divides either pb - aq or pb + aq since:
(pb - aq)(pb+aq) = (p² + 3q²)(b² - q²f) [From Euclid's Lemma and steps (1), (2)]

(4) So that there exists a value F such that:
(p² + 3q²)F equals either pb + aq or pb - aq

(5) Now, from multiplication of polynomials with this form, we know that:
(p² + 3(±q)²)(a² + 3b²) = (pa ± 3qb)² + 3(pb ± aq)²

(6) So, p² + 3q² divides pa ± 3qb since:
(pa ± 3qb)² = (p² + 3q²)(a² + 3b²) - 3(pb ± aq)² =
(p² + 3q²)[(a² + 3b²) - 3(F)²]

(7) So, there exists c,d such that:
pa ± 3qb = c(p² + 3q²)
pb ± aq = d(p² + 3q²)

(8) Which means that:
(pa ± 3qb)² + 3(pb ± aq)² =
(c * (p² + 3q²))² + 3[d * (p² + 3q²)]²

(9) Putting it altogether means that:
(a² + 3b²) divided by (p² + 3q²) =
(pa ± 3qb)² + 3(pb ± aq)² divided by (p² + 3q²)² [From step (5)]
= [c * (p² + 3q²)]² + 3[d * (p² + 3q²)]² divided by (p² + 3q²)² =
c² + 3d²

QED

Fermat's Last Theorem: n = 3: More a2 + 3b2

Today's blog presents another lemma associated with the polynomial a² + 3b². This lemma is used in the proof for Fermat's Last Theorem: n=3 that was first presented by Leonhard Euler. It is believed that Pierre de Fermat knew this proof but it took the work of a genius like Euler to recreate it. You can see the full proof for Fermat's Last Theorem n=3 by starting here.

Lemma: if a² + 3b² has an odd factor that is not of this form, then the quotient has an odd factor which is not of this form.

In other words, given the following:

• There exists f which is a factor of a value a² + 3b²
• f does not have the form p² + 3q²

Then, there exists:

• A value F such that fF = a² + 3b²
• A value f' such that f' divides F and such that it does not have the form p² + 3q²

Here is the proof:

(1) So there exists f,g such that fg = a² + 3b², f is odd and f is not in the form p² + 3q²

(2) Let's assume that all of the odd factors of g have the form p² + 3q²

(3) Now g = a series of primes p₁ * p₂ * ... * p_n [By the Fundamental Theoreom of Arithmetic]

(4) In this series, we can replace all instances of 2 with instances of 4.

(a) We know that if 2 divides a² + 3b², then 4 divides it. [See here for proof]
(b) We know that f is odd so each instance of 4 necessarily divides g

(5) Now we can divide all instances of 4 from g and from a² + 3b² and still have a result in the form of p² + 3q². [See here for proof]

(6) Likewise, we can divide all odd primes from g since we are assuming that all odd factors take the form p² + 3q². [The proof is found here.]

(7) But then this leaves f = p² + 3q² which is a contradiction.

(8) Therefore, we reject our assumption.

QED

Fermat's Last Theorem: n = 3: a2 + 3b2

The essence of Euler's proof for Fermat's Last Theorem, n = 3, is realizing the properties of values that can be represented by the formula: a² + 3b².

In today's blog, I will present a lemma that illustrates one of the surprising properties of the above formula.

This blog will continue the details of the proof that was begun in a previous blog.

Lemma: If gcd(a,b)=1, then every odd factor of a² + 3b² has this same form.

In other words, for every odd factor of a² + 3b², there exists c,d such that the odd factor = c² +3d²

(1) Let x be a positive, odd factor of a² + 3b²

(2) Then, there exists a value f such that:
a² + 3b² = xf

(3) We can assume that x is greater than 1 (since if x = 1 it's only factor is itself and 1 = 1² + 3(0)².)

(4) There exists integers m,n such that:

a = mx ± c
b = nx ± d

where c,d can be positive or negative.

(5) Now, we can assume that c,d have absolute values that are less than (1/2)x.

(a) From the Division Algorithm (see Theorem 1, here), we know that c is less than x.

(b) Assume that c ≥ (1/2)x

(c) c' = x - c = -(c - x)

(d) a = mx + c = (m+1)x + c - x = (m+1)x - (x - c) = (m+1)x - c'

(e) abs(c') is less than (1/2)x since c' = x - c

(6) From step #4, we have:

a² + 3b² =

(mx ± c)² + 3(nx ± d)² =

m²x² ± 2mxc + c² + 3n²x² ± 6nxd + 3d² =

= x(m²x ± 2mc + 3n²x ± 6nd) + c² + 3d²

(7) So x divides c² + 3d² since from step #1, since x is a factor of a² + 3b².

(8) So, there exists y such that:

c² + 3d² = xy

(9) Now from step #5 above, we have:

xy = c² + 3d² is less than [(1/2)x]² + 3[(1/2)x]² = (1/4)x² + (3/4)x² = x².

(10) Now, we can conclude that y is less than x from:

(a) Since c², d² are nonnegative, it follows that xy is nonnegative.

(b) From step #9, xy is less than x²

(c) Since x is positive, the only way that this can be true is if y is less than x.

(11) We also know that c² + 3d² ≠ 0 because:

(a) Assume c² + 3d² = 0.

(b) Then c=0, d=0 since c² and 3d² are both nonnegative.

(c) But then: a = mx, b = nx and x divides both a,b.

(d) Which contradicts gcd(a,b)=1 so we reject our assumption.

(12) Let g = gcd(c,d). We know there exists C,D such that c = gC, d=gD, gcd(C,D)=1. [From the properties of greatest common denominators]

(13) Now we also know that g² divides y because:

(a) xy =c² +3d² = (gC)² + 3(gD)² = g²(C² + 3D²)

(b) Assume there is a prime p that divides g but doesn't divide y.

(c) Then p divides g and p divides x

(d) Then, there exists X,G where x = Xp, g = Gp

(e) And, p divides a and b since

a = mx + c = mpX + GpC = p(mX + GC)

b = nx + d = npX + GpD = p(nX + GD)

(f) But this is impossible since a,b are coprime.

(g) So, there is no prime p which divides g but does not divide y.

(h) Which proves that g divide y and further that g² divides y

(14) Since g² divides y, there exists z such that:

y = g²z

(15) Now, it follows that there exist C,D such that:

xz = C² + 3D² where gcd(C,D)=1

(a) xy = g²(C² + 3D²) [from step #13a above]

(b) gcd(C,D) = 1 [from step #12 above]

(c) Then substituting z from step #14 gives us:

xz = C² + 3D²

(16) Now we have enough to conclude that x is of the form p² + 3q²

(a) Assume that x is not of this form.

(b) From step #15, we have xz = C² + 3D² where gcd(C,D)=1.

(c) Then there must exist w such that w divides z and w is not of the form p² + 3q² [See here
for the proof of this lemma]

(d) Now, w ≠ 1 since 1 = 1² + 3(0)²

(e) So, w is smaller than z [since w is greater than 1 and w divides z]

(f) But then w is less than x [since z is less than y (step #14, since y = g²z) and y is less than x (step #10)]

(g) But now, we have proven that the existence of x proves the existence of a smaller factor w which divides a smaller value of the same form.

(h) We can use the same argument to presuppose a value w' which is smaller than w and another value w'' which is smaller than w'. In other words, we have a contradiction by the method of infinite descent.

QED