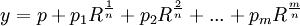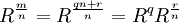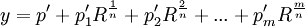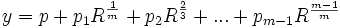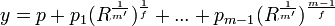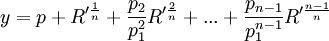Abel's Proof: Step Two

In today's blog, I will cover step 2 of the original proof by Niels Abel on the quintic equation. The content in today's blog is taken from Peter Pesic's excellent book Abel's Proof.

In Step 2, Abel shows that if the general quintic equation has a solution expressible in radicals, then all irrational functions in this formula are expressible as rational functions of the roots.

This step was the gap in Paolo Ruffini's proof.

Lemma 1:

The equation:

[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁵ -a[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁴ + ... + e = 0

can be reduced to:

0 = q + q₁R^(1/m) + q₂(R^(2/m)) + ... + q_m-1R^(m-1)/m

where q, q₁, q₂, ... are rational functions based on the quantities a,b,c,d,e,p,p₂, ... and R.

Proof:

(1) We start with the following:

[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁵ -
a[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁴ + ... + e = 0

where a,b,c,d,e are rational coefficients.

(2) Since the equation does not involve any additional radicals, we can see that it can be ordered around sums of xR^(u/m) where x is a rational function of p,R,a,b,c,d,e and u is an integer.

(3) If u is greater m, then there exists q,r such that u=qm + r where r ≤ m-1.

(4) xR^(u/m) = xR^(qm+r)/m = xR^q*R^(r/m)

(5) If we set x' = x*R^q, then we have:

xR^(u/m)=x'R^(r/m) where r is less than m.

(6) So, if we number each of the x', then we are left with:

[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁵ - a[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁴ + ... + e =x'₀R^(0/m) + x'₁R^(1/m) + ... + x'_m-1R^(m-1)/m

where x_i is a rational function of a,b,c,d,e,p,p_i,R

QED

Corollary 1.1:

If R^1/m is not expressible in rationals, then q, q₁, q₂, ... all = 0.

Proof:

(1) Let z = R^(1/m)

(2) So, we have two equations:

z^m - R = 0

and

q + q₁z + ... + q_m-1z^m-1 = 0

(3) Using Abel's Lemma (see Lemma 2, here), we can conclude that z^m - R=0 is not reducible in rationals.

(4) Now, since R^(1/m) is a root for both equations, we can use Abel's Irreducibility Theorem (See Thereom 3 here) to conclude that q, q₁, ..., q_m-1 must all equal 0.

QED

Lemma 2:

If:





...



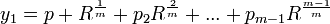
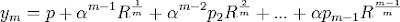
Then:

p = (1/m)(y₁ + y₂ + ... + y_m)

Proof:

(1) y₁ + y₂ + ... + y_m =

mp + (1 + α + α² + ... + α^m-1)R^(1/m) + p₂(1 + α + α² + ... + α^m-1)R^(2/m) + ... + p_m-1(1 + α + α² + ... + α^m-1)R^(m-1)/m

(2) Since (1 + α + α² + ... + α^m-1)=0 (see Lemma 2, here), we are left with:

mp = y₁ + y₂ + ... + y_m

(3) So that we have:

p = (1/m)(y₁ + y₂ + ... + y_m)

QED

Lemma 3:

If:





...



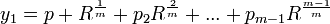
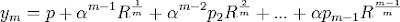
Then:

R^(1/m) = (1/m)(y₁ + α^m-1y₂ + ... + αy_m)

Proof:

(1) y₁ + α^m-1y₂ + α^m-2y₃ + ... + αy_m =

= (1 + α + α² + ... + α^m-1)p + mα^mR^(1/m) + p₂α^m(1 + α + α² + ... + α^m-1)R^(2/m) + .... + α^mp_m-1(1 + α + α² + ... + α^m-1)R^(m-1)/m

(2) Since α^m = 1 and (1 + α + α² + ... + α^m-1)=0 (see Lemma 2, here), we are left with:

mR^(1/m) = y₁ + α^m-1y₂ + α^m-2y₃ + ... + αy_m

QED

Lemma 4:

If:





...



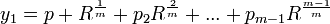
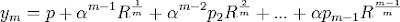
Then:

p_iR^(i/m) = (1/m)(y₁ + α^m-iy₂ + ... + αⁱy_m)

Proof:

(1) For any i, we have:

y₁ + α^m-iy₂ + ... + αⁱy_m =

= (1 + α + α² + ... + α^m-1)p + mα^m(1 + α + α² + ... + α^m-1)R^(1/m) + ... + p_iα^mR^(i/m) + .... + α^mp_m-1(1 + α + α² + ... + α^m-1)R^(m-1)/m

(2) Since α^m = 1 and (1 + α + α² + ... + α^m-1)=0 (see Lemma 2, here), we are left with:

mp_iR^(i/m) = y₁ + α^m-iy₂ + α^m-(i+1)y₃ + ... + αⁱy_m

QED

Theorem 5:

Let :



be a solution to the general quintic equation:

y⁵ - ay⁴ + by³ - cy² + dy - e =0

where p,p₂,..., p_m-1, R are expressible in radicals, m is a prime, and R^(1/m) is irrational.

Then the m roots are:





...



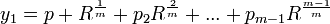
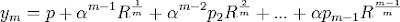
Proof:

(1) We can represent the general quintic equation as follows:

y⁵ + ay⁴ + by³ + cy² + dy - e = 0

(2) If we now insert this solution into the equation at step #1, we are left with:

[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁵ -
a[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁴ + ... + e = 0

(3) Using Lemma 1 above, we can reduce the above result to get:

0 = q₀ + q₁R^(1/m) + q₂R^(2/m) + ... + q_m-1R^(m-1)/m

where q₀, q₁, q₂, ... are rational functions based on the quantities a,b,c,d,e,p,p₂, ... and R.

(4) Using Corollary 1.1 above, we know that:

q₀, q₁, ..., q_m-1 all equal 0.

(5) Now, it is also clear that R^(1/m) has m different solutions where if R^(1/m) is one solution, the solutions are:

R, αR, α²R,..., α^m-1R where α is a m-th root of unity.

(6) So, if we use our equation for y, we are left with m roots:





...



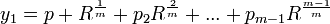
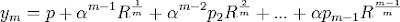
QED

Corollary 5.1:

Let :



be a solution to the general quintic equation:

y⁵ - ay⁴ + by³ - cy² + dy - e =0

where p,p₂,..., p_m-1, R are expressible in radicals, m is a prime, and R^(1/m) is irrational.

Then:

p,p₂, ..., p_m-1, R^(1/m) are rational functions of α, and the roots: y₁, y₂, ..., y₅

Proof:

(1) From Theorem 5 above, we have the m roots as:





...



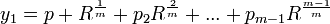
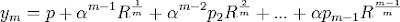
(2) Now, we complete this proof using Lemma 2, Lemma 3, and Lemma 4, since now we have:

p = (1/m)(y₁ + y₂ + ... + y_m)

R^(1/m) = (1/m)(y₁ + α^m-1y₂ + ... + αy_m)

p_iR^(i/m) = (1/m)(y₁ + α^m-iy₂ + ... + αⁱy_m)

QED

Corollary 5.2:

Let :



be a solution to the general quintic equation:

y⁵ - ay⁴ + by³ - cy² + dy - e =0

where each R is itself expressible in the same form such as:



Then:

there exists t, t_1,1, ... t_5,4 such that:

v^(1/n) = t + t_1,1y₁ + ... + t_1,4y₁⁴ + ... + t_5,1y₅ + ... + t_5,4y₅⁴

where v is any nested element of the above form.

Proof:

(1) If v is at the top level, then from Corollary 5.1 above, we know that:

v^(1/m) = (1/m)(y₁ + α^m-1y₂ + ... + αy_m)

(2) Likewise, if v is at the first nested level with R at the top level, then:



(3) Using the same logic as Corollary 5.1 above, we where treat R₁ = R, R₂ = αR, ..., R₅ = α⁴R, then we have:

v^(1/n) = (1/n)(R₁ + α^n-1R₂ + ... + αR_n)

(4) Then substituting the equation in step #1 above gives us:

v^(1/n) = (1/n)({(1/m)[y₁ + ... + αy_m]}⁵ + ... + α*α⁴{(1/m)[y₁ + ... + αy_m]}⁵)

(5) We can keep doing this substitution as far as needed so that we can assume that any nested form of v^(1/n) is a function of y₁, y₂, ..., y₅

(6) Finally, we can assume that no power is greater than m-1 since each root is a solution to the quintic equation and we can assume that:

y_i⁵ - ay_i⁴ + by_i³ - cy_i² + dy_i - e =0

(7) And further that:

y_i⁵ = ay_i⁴ - by_i³ + cy_i² - dy_i + e

QED

References

• Peter Pesic, Abel's Proof: An Essay on the Sources and Meaning of Mathematical Unsolvability, Appendix B, The MIT Press, 2004

Abel's Lemmas on Irreducibility

In today's blog, I present a few lemmas that Niels Abel published on irreducibility. These lemmas are used in Abel's proof on the insolvability of the quintic equation.

The content in today's blog is taken from 100 Great Problems of Elementary Mathematics by Heinrich Dorrie.

Definition 1: expressible in rationals

"A number or equation is expressible in rationals if it is expressible using only addition, subtraction, multiplication, and division of integers."

Definition 2: rational functions

A function f(x) is rational if its coefficients are all rational numbers.

Definition 3: degree of a polynomial

The degree of a polynomial is the highest power of the polynomial that has nonzero coefficients.

Definition 4: reducible over rationals

A function f(x) with coefficients in the rational numbers is said to be reducible over rationals if it can be divided into a product of polynomials with lower degree and rational coefficients.

Definition 5: free term or constant term of a polynomial

The free term or constant term of a polynomial is the value that is not bound to an unknown.

Lemma 1: The free term is equal to the product of roots.

Proof:

(1) Let a₀xⁿ + a₁x^n-1 + ... + a_n-1x + a_n be an n degree polynomial.

(2) By the Fundamental Theorem of Algebra (see Theorem, here), we know that there are n roots such that:

a₀xⁿ + a₁x^n-1 + ... + a_n-1x + a_n = (x - r₁)*(x - r₂)*...*(x - r_n)

(3) Now, it is clear that of the products in step #2, the only term that does not include x is the product of all the roots.

QED

Lemma 2: Abel's Lemma

The equation x^p = C where p is a prime number is irreducible over rationals when C is a rational number not the pth power of a rational number

Proof:

(1) Assume that x^p = C is reducible into rational functions.

(2) Then, there exists f(x),g(x) such that x^p - C = f(x)g(x) where f(x),g(x) are rational functions of lower degree.

(3) We know that the roots to x^p - C=0 are r, rα, rα², ... rα^p-1 where r is one of the roots and α is a pth root of unity since:

(rαⁱ)^p = (r^p)(αⁱ)^p = (r^p)(α^p)ⁱ = r^p*(1)ⁱ = r^p

(4) Let A,B be the the free terms for f(x) and g(x) respectively.

(5) Since a free term is the product of a function's root (see Lemma 1 above), we know that A*B = (r)*(rα)*(rα²)*...*(rα^p-1) = ± C

(6) We can see that C = r^p since:

(a) If p=2, then α=-1 and the roots are r*(-r) = -r²

(b) If p is a prime ≥ 3, then using the summation formula (see Corollary 2.1, here), we have:

C = r^pα^{[(1/2)(p)(p-1)]}

(c) Since p-1 is even, we have:

C = r^p(α^p)^(1/2)(p-1) = r^p(1)^(1/2)(p-1) = r^p

(7) Likewise, there exists μ, M, ν, N such that:

A = r^μα^M

B = r^να^N

(8) Since there are p instances of r in the product in step #5, we know that:

μ + ν = p

(9) We further know that gcd(μ,ν) = 1 since:

(a) Assume that gcd(μ,ν) = f which is greater than 1.

(b) So μ = mf and ν = nf

(c) Then p = mf + nf = f(m+n)

(d) But p is prime so this is impossible and f=1.

(10) Using Bezout's Identity (see Lemma 1, here), we know that there exists h,k such that:

μh + νk = 1

(11) Now let's define a rational number K as K = A^h*B^k

(12) So that K= A^h*B^k = r^hμα^M*r^kνα^N = r^{(hμ + kν)}α^hM+kN = rα^hM+kN

(13) But then K^p = (rα^hM+kN)^p = r^p*(α^p)^hM+kN = r^p

(14) But this is impossible since we selected an integer C that is not a p-th power.

QED

Theorem 3: Abel's Irreducibility Theorem

Let f(x) be irreducible over rationals.

If one root of the equation f(x) is also a root of the rational equation F(x)=0

Then:

All the roots of f(x) are roots of F(x) and F(x) can be divided by f(x) without a remainder.

Proof:

(1) Using Euclid's Greatest Common Divisor Algorithm for Polynomials (see Theorem 3, here), we are left with:

V(x)F(x) + v(x)f(x) = g(x)

(2) If F(x) and f(x) have no common divisor, then g(x) is a constant. That is, g(x) = g₀ where g₀ is the free term.

(3) If f(x) is irreducible and a root r of f = 0 is also a root of F(x), then there exists a common divisor of at least the first degree (x-r)

(4) Since f(x) is irreducible, f₁(x) must equal a constant and f(x)=g(x)*f₁(x) = g(x)*f1₀.

(5) Then, F(x)=F₁(x)*g(x) = F₁(x)*f(x)*f1₀

(6) Thus, F(x) is divisible by f(x) and vanishes for every zero point of f(x).

QED

Corollary 3.1:

If a root of an equation f(x)=0 which is irreducible in rational numbers is also a root of F(x)=0 in rational numbers of lower degree than f, then all the coefficients of F are equal to zero.

Proof:

(1) Assume that at least one coefficient of F is not zero.

(2) Then F is a polynomial with a degree of at least 1.

(3) Since there is a root that divides both f(x) and F(x) and since f(x) is irreducible over rationals, we can use Theorem 3 above to conclude that every root of f(x) divides F(x).

(4) But F(x) has a lower degree than f(x) which is impossible.

(5) So we reject our assumption at step #1 and conclude that all coefficients of F must be 0.

QED

Corollary 3.2:

If f(x)=0 is an irreducible over rationals, then there is no other equation irreducible over rationals that has a common root with f(x)=0.

Proof:

(1) Let f(x) and g(x) be functions irreducible over rationals.

(2) Assume that f(x) and g(x) have a common root r.

(3) Then we can use Theorem 3 above to conclude that f(x) divides g(x) and g(x) divides f(x).

(4) But if f(x) divides g(x) and g(x) divides f(x), it is clear that f(x) = g(x).

QED

References

• 100 Great Problems of Elementary Mathematics (Dover, 1965)

Abel's Form of a General Solution by Radicals

The first step in Niel Abel's 1824 proof on the insolvability of the general quintic equation is the statement that if a general solution to the quintic exists, it can be assumed to have the following form:



where m is a prime number and R, p₂, ..., p_m-1 are all functions of this same form finitely nested and are functions of the coefficients of the general quintic equation.

Today's content is taken from Peter Pesic's Abel's Proof.

Lemma 1:

If a mathematical expression is expressible by radicals, then it is stateable in the form:

(A₁ + A₂ + ... + A_m)/(B₁ + B₂ + ... + B_n) where each A_i, B_i are expressible by radicals.

Proof:

(1) First, I show that if a mathematical expression is minimally expressible by radicals, then it is expressible by the desired form:

a + b = (a + b)/(1)

a - b = (a - b)/(1)

a * b = (a*b)/(1)

a/b = (a)/(b)

√a = (a^(1/2))/(1)

(2) By the above analysis, we know that it works to at least the minimum number of operations. Let's assume that it works only up to n operations.

(3) To complete the proof, I will show that I can add an additional operation to the above form and maintain the above form. I only need to show that this is true for addition, subtraction, multiplication, division, and radicals:

(±)a + (A₁ + ... + A_m)/(B₁ + ... + B_n) =

= (A₁ + ... + A_m + (±)a[B₁ + ... + B_n])/(B₁ + ... + B_n)

a*(A₁ + ... + A_m)/(B₁ + ... + B_n) =

= (a*A₁ + ... + a*A_m)/(B₁ + ... + B_n)

(1/a)*(A₁ + ... + A_m)/(B₁ + ... + B_n) =

= (A₁ + ... + A_m)/(a*B₁ + ... + a*B_n)

[ (A₁ + ... + A_m)/(B₁ + ... + B_n)]^(1/a) = [(A₁ + ... + A_m)]^(1/a)/[(B₁ + ... + B_n)^(1/a)]


QED

Lemma 2:

If the general quintic equation has a solution which has the form:

y = (A₁)^(c₁/d₁) + (A₂)^(c₂/d₂) + ... + (A_n)^(c_n/d_n)

where each A_i is expressible by radicals

then it can be put into the following form:



where R, p₁, ..., p_m-1 are all functions of this same form finitely nested.

Proof:

(1) By assumption, we can state the solution to the general quintic equation in the following form:

y = (A₁)^(c₁/d₁) + (A₂)^(c₂/d₂) + ... + (A_n)^(c_n/d_n)

where each A_i are expressible as radicals.

(2) Now, if we set each A'_i to (A_i^c_i), then we get:

y = (A'₁)^(1/d₁) + (A'₂)^(1/d₂) + ... + (A'_n)^(1/d_n)

(3) Since, the expression has finite complexity, it follows that there can only be a finite number of expressions of the form (A'_i)^(1/d_i)

(4) So, there exists a number k such that:

[number of radicals in y] = k.

(5) Now, we can put this expression in the desired form by setting:

R = A'₁

m = d₁

p₁ = 1

p = (A'₂)^(1/d₂) + ... + (A'_n)^(1/d_n)

p_i = 0 where i ≠ 1.

(6) This changes y into

y = p + p₁R^(1/m)

(7) Now, it is clear that:

[number of radicals in p] + [number of radicals in R] = [number of radicals in y] - 1 = k-1

(8) And since we do the same refactoring for all in radicals in p and all radicals in R and since there are only a finite amount of them, we can put all radicals into the desired form.

(9) To complete the proof, we need only show that an equation without radicals can also be put into this form.

(10) So assume y does not have radicals. That is:

[number of radicals in y] = 0

(13) Then let:

p = A₁^c₁ + A₂^c₂ + ... + A_n^c_n

with each p_i=0.

QED

Corollary 2.1:

If the general quintic equation has a solution, then it can be put into the following form:



where R, p₁, ..., p_m-1 are all functions of this same form finitely nested.

Proof:

(1) Using Lemma 1 above, if the solution to the general equation is expressible by radicals, then it follows that y is expressible as:

y = (A₁ + A₂ + ... + A_m)/(B₁ + B₂ + ... + B_n) where each A_i, B_i are expressible by radicals.

(2) Let:

T = A₁ + A₂ + ... + A_m

W = B₁ + B₂ + ... + B_n

such that we have:

y = T/W

(3) Using Lemma 2 above, we know that T,W can be put in the following forms:





(4) Let:

W(x) = w₀ + w₁x + w₂x² + ... + w_vx^v

α = an n-th root of unity. (that is, α ≠ 1 and αⁿ=1)

(5) So, we now define W₀, W₁, ..., W_n-1 with:

W₀ = W(R^(1/n)) = W

W₁ = W(αR^(1/n))

W₂ = W(α²R^(1/n))

...

W_n-1 = W(α^n-1R^(1/n))

(6) So, if we multiply (W₁*...*W_n-1)/(W₁*...*W_n-1), we get:

Y = (T*W₁*...*W_v-1)/(W*W₁*...*W_v-1)

(7) Multiplying W*W₁*...*W_n-1 out, we get:

W*W₁*W₂*...*W_n-1 =

= (w₀ + w₁R^(1/n) + w₂R^(2/n) + ... + w_vR^(v/n))*(w₀ + αw₁R^(1/n) + α²w₂R^(2/n) + ... + α^vw_vR^(v/n))*(w₀ + α²w₁R^(1/n) + α⁴w₂R^(2/n) + ... + α^2vw_vR^(v/n))*...*(w₀ + α^(n-1)w₁R^(1/n) + α^2(n-1)w₂R^(2/n) + ... + α^v(n-1)w_vR^(v/n)) =

=w₀ⁿ + αw₀^n-1w₁(1 + α + α² + ... + α^n-1) + ... α²w₀^n-2w₂R^(2/n)(1 + α + α² + ... + α^n-1) + ...

(8) Now, since (1 + α + α² + ... + α^n-1) = 0 [See Lemma 2, here], we have:

W*W₁*W₂*...*W_n-1 = v₀ⁿ

(9) If w₀ⁿ contains radicals, then we set W=w₀ⁿ and we repeat the process.

(10) Since the original W has only a finite nesting of radicals, it follows that eventually we will reach a w₀ⁿ that does not contain any radicals and we set each of the resulting t_i = t_i/(w₀ⁿ)

QED

Lemma 3:

For the following expression



We can assume that m is less than n.

Proof:

(1) Assume that m is not less than n.

(2) Then, we there exists q,r such that (see Theorem 1, here):

m = qn + r

where q ≥ 1, and 0 ≤ r ≤ n-1

(3) Then:



(4) Now, if we define p'_i so that:

p'_i = p_i*R^q, then we are left with:



where m is less than n.

QED

Lemma 4:

For any equation of the following form:



We can assume that m is prime.

Proof:

(1) Assume that m is not prime.

(2) Then m consists of a finite number of primes. [See Theorem 3, here for proof of the Fundamental Theorem of Arithmetic]

(3) Let's take out the first prime which I will call f. So that we have m = f*m'.

(4) So we can restate y as:



(5) Now, we can redefine each R such that:

R = R^(1/m')

(6) After this, we are left with an equation of the desired form.

QED

Theorem 5: Abel's General Form

If a general solution to the quintic exists, it can be assumed to have the following form:



where m is a prime number and R, p₁, ..., p_m-1 are all functions of this same form finitely nested and are functions of the coefficients of the general quintic equation.

Proof:

(1) By Corollary 2.1 above:

If the general quintic equation has a solution, then it can be put into the following form:



where R, p₁, ..., p_m-1 are all functions of this same form finitely nested.

(2) By Lemma 3 above, we can assume that m is less than n.

(3) By Lemma 4 above, we can assume that n is prime.

(4) Let R' = R/[p₁ⁿ]

(5) Then we have:


(6) Now, for all this nesting of equations of this form, at the end, each R' must be in a function of the coefficients of the general quintic equation.

(7) If not, then it does not represent a solution to the general quintic since a solution consists of determining each of the roots based on the coefficients given.

QED

References

• Peter Pesic, Abel's Proof: An Essay on the Sources and Meaning of Mathematical Unsolvability, Appendix B, The MIT Press, 2004.

Cauchy's Theorem on the Permutations of a Function

It is perhaps a bit surprising that a study of functions with multiple parameters led to the proof by Niels Abel that the quintic equation was not solvable by radicals.

In today's blog, I will focus on a very interesting result from Augustin-Louis Cauchy. He discovered that there are limits to the number of values a function of multiple parameters can take when you change the order of the parameters. The content in today's blog is taken from Peter Pesic's Abel's Proof.

Joseph-Louis Lagrange had shown that the number of values a function of n parameters can take from permuting parameters will necessarily divide n!. I went over this result in a previous entry.

Cauchy found additional limits on the number of values a function can take. For a function with n parameters, if p is the highest prime that divides n, then the function can take 1, 2, or at least p possible values from permuting the order of its parameters.

That a function with n parameteres can take 1 value is easy to show. Consider the following function:

f(x₁, x₂, ..., x_n) = x₁ + x₂ + ... + x_n

Clearly, swapping any two parameters doesn't change the value so it is clear that no permutation will change its value. In this case, the function of n parameters can only take on 1 value.

It is also easy to show a function of n parameters can take on 2 values. Consider the following function:

f(x₁, x₂, ..., x_n) = (x₁ - x₂) *(x₁ - x₃)*... *(x₁ - x_n)*...*(x_n-1 - x_n)

Now, any swap of two parameters will keep the absolute value but change the sign of the function. So, the absolute value stays the same.

So, this is where Cauchy's Theorem comes in. Cauchy proves that if a function of n parameters takes on more than 2 values, then it necessarily takes on at least p values where p is the highest prime dividing n.

Here's an example where this occurs. Consider the following function:

f(x₁, x₂, x₃, x₄, x₅) = (x₁ + x₂ + x₃ + x₄) - x₅

How many values can this function take on if we permute the parameters? Since swapping x₅ changes the value of the function, we can see that there are at least 5 possible values (1 + 4) that the function can take.

Let's start out with some definitions:

Definition 1: f(P)^u

Let P be a permutation and let f(P)^u represent the value of the function after the permutation P is applied to the function f, u times. I will use f(P)⁰ to mean that the permutation has been applied 0 times.

Definition 2: Order of a Permutation

A permutation P is said to be of order k if P^k(f(x₁, ..., x_n)) = f(x₁, ..., x_n). Using the above notation, this means that f(P)^k = f(P)⁰.

In other words, the permutation after being applied k times return the function to its original ordering of the parameters.

Definition 3: f(P)^-u

By -u, I mean the inverse of the permutation. Since each permutation is one-to-one and onto, (see here for review if needed), it follows that it has an inverse which is also a permutation. f(P)^-u means that we apply the inverse of the permutation u times.

This gives us the result that if we apply the permutation P u times to f(P)^-u, we are left with f(P)^-u+u = f(P)⁰

Now, I will use these definitions in the following lemmas from Cauchy:

Lemma 1:

Let f be a function that takes n parameters.

Let p be the largest prime that divides n

Let m be the number of values that f takes on when we permute the order of f's parameters.

If m is less than p, then any permutation of order p will leave the value of f unchanged.

Proof:

(1) Let P be a permutation of order p such as (x₁ → x₂ → x₃ → ... → x_p → x₁)

(2) So, we have f(P)^p = f(P)⁰

(3) Now, let's consider the set of p-1 orderings that f takes as we apply P to f:

f(P)⁰, f(P)¹, f(P)², ..., f(P)^p-1

(4) Since we are assuming that m is at most p-1, it follows that two of these values must be the same.

(5) Let's label them r and r' where 0 ≤ r' ≤ p-2 and 1 ≤ r ≤ p-1 and further r' is less than r so that:

f(P)^r = f(P)^r'

(6) Now since both r, r' are less than p, we know that p-r ≥ 1.

(7) Now, if we apply the permutation P to both values (p-r) times, we get:

f(P)^r+p-r = f(P)^r'+p-r

(8) Since r+p-r = p and f(P)^p = f(P)⁰, we are left with:

f(P)⁰ = f(P)^r'+p-r

(9) Let j = r'+p-r so that we have:

f(P)⁰ = f(P)^j

(10) We can see that f(P)⁰ = f(P)^bj where b is any integer that we choose since:

(a) For b=1, this is clearly the case from step #9.

(b) We assume it is true up to b-1 so that:

f(P)⁰ = f(P)^(b-1)j = f(P)^bj-j

(c) Now, we apply P to each side j times so that we have:

f(P)^0+j = f(P)^bj-j+j

(d) This gives us that:

f(P)^j = f(P)^bj

(e) Applying step #9 gives us:

f(P)⁰ = f(P)^bj

(f) We can make the same argument for the case when b is negative.

(g) Let P^-1 be the inverse permutation of P.

(h) Apply P^-1 j times to each value in step #9 gives us:

f(P)^-j = f(P)⁰

(h) Now, we assume that it is true up to b-1 so that we have:

f(P)^-j(b-1) = f(P)^-bj+jf(P)⁰

(i) Now, we apply P^-1 j times to each side to get:

f(P)^-bj = f(P)^-j

(j) Applying step #10i gives us:

f(P)^-bj = f(P)⁰

(11) Now, we know that j is a number less than p since j = r' + p - r and r is greater than r'.

(12) Since p is prime, it follows that gcd(p,j)=1 and using Bezout's Identity, we know that there exists integers a',b such that:
a'p + bj = 1

(13) Let a = -a', then we have:

-ap + bj = 1

which is the same as:

bj = ap + 1

(14) Appyling this equation to f gives us:
f(P)^bj = f(P)^ap+1

(15) From step #10 this gives us that:

f(P)⁰ = f(P)^ap+1

(16) But from step #2, this gives us that:

f(P)⁰ = f(P)^ap
(17) This means that:

f(P)^ap = f(P)^ap+1

(18) But this is only possible if P doesn't change the value of the function.

QED

Let's explore Lemma 1 in more detail. Consider our function with 2 values where:

f(x₁, x₂, x₃) = (x₁ - x₂)*(x₁ - x₃)*(x₂ - x₃)

Since n=3, the highest prime is 3. Let's see how many permutations there are with the order of 3.

P = (x₁ → x₂ → x₃ → x₁)

So, applying P once gives us:

f(P)¹ = (x₂ - x₃)*(x₂ - x₁)*(x₃ - x₁) = (x₂ - x₃)*(-1)*(x₁ - x₂)*(-1)*(x₁ - x₃) = (x₁ - x₂)*(x₁ - x₃)*(x₂ - x₃)

So, we see that Lemma 1 holds.

Now, it turns out that this lemma has a surprising corollary.

Corollary 1.1:

Let f be a function that takes n parameters.

Let p be the largest prime that divides n

Let m be the number of values that f takes on when we permute the order of f's parameters.

If m is less than p, then any permutation of order 3 will leave the value of f unchanged.

Proof:

(1) Let P₁ be a permutation of order 3 which we can define as x_i1 → x_i2 → x_i3 → x_i1

(2) I will show that it is equivalent to application of two permutations of order p.

(3) Let P₂ be the permutation of order p such that:

x_i1 → x_i2 → ... → x_ip

We can view this as (1234...p)

(4) Let P₃ be another permutation of order p such that:

x_i2 → x_i3, x_i3 → x_i1, x_i4 → x_i2, x_i5 → x_i4, x_i6 → x_i5, ..., x_i1 → x_ip

We can view this as (1p...5423)

(5) Now, if we perform the first permutation (P₂) and then the second (P₃), we get:

x_i1 → x_i2 → x_i3, x_i2 → x_i3 → x_i1, x_i3 → x_i4 → x_i2, x_i4 → x_i5 → x_i4, x_i5 → x_i6 → x_i5, ..., x_ip → x_i1 → x_ip

(6) In other words, we have the three-order permutation:

x_i1 → x_i2 → x_i3 → x_i1

(7) Since both order-p permutations of step #3 and step #4 do not change the value of the function and since P₁ = P₃(P₂), it follows P₁ does not change the value of the function.

QED

Let's see this result in action. Let's revise our example above to now have 5 parameters so that we have n=5, p=5 and the number of different values are 2:

f(x₁, x₂, x₃, x₄, x₅) = (x₁ - x₂)*(x₁ - x₃)*...*(x₂ - x₃)...*(x₄ - x₅)

Now, let's see what happens when we apply the following permutation of order 3:

P = (x₁ → x₂ → x₃ → x₁)

We get:

f(P)¹ = (x₂ - x₃)*(x₂ - x₄)*...*(x₄ - x₅)

Now, we only need to consider the cases where the the first element is greater than the second element. This occurred twice so that we now have:

(x₂ - x₁)*(x₃ - x₁)

But if it occurs only twice, then we have:

(-1)*(x₁ - x₂)*(-1)*(x₁ - x₃) = (x₁-x₂)*(x₁ - x₃)

So, we see that the corrollary holds.

Cauchy was able to take this result one step farther:

Corollary 1.2:

Let f be a function that takes n parameters.

Let p be the largest prime that divides n

Let m be the number of values that f takes on when we permute the order of f's parameters.

If m is less than p, then application of any two permutation of order 2 will leave the value of f unchanged.

Proof:

(1) Let P₁ be an order-2 permutation such that:

x_j1 → x_j2

(2) Let P₂ be an order-2 permutation with overlap with P₁

x_j2 → x_j3

(3) So, we can define an order-3 permutation that is equivalent to the application of these two permutations of order 2:

x_j1 → x_j2 → x_j3

(4) Again, we know that application of the two overlapping order-2 permutations cannot change the value. If they did, this would imply that the above order-3 permutation would also change the value which goes against Corollary 1.1 above.

(5) Let's redefine P₂ so that it does not overlap with P₁ so that:

x_j3 → x_j4

(6) But in this case, it is equivalent to application of two order-3 permutations.

(7) Let us define P₃ as:

x_j1 → x_j2→ x_j3

(8) And define P₄ as:

x_j3 → x_j1 → x_j4

(9) We can see that they are equivalent since we now have:

x_j1 → x_j2 → x_j2

x_j2 → x_j3 → x_j1

x_j3 → x_j1 → x_j4

x_j4 → x_j4 → x_j3

(10) Again, the application of two order-2 permutations cannot change the value since the application of two order-3 permutations cannot change the value.

QED

Now, we are ready for Cauchy's main theorem.

Theorem 2: For a function with n parameters, if p is the highest prime that divides n, then the function can take 1, 2, or at least p possible values from permuting the order of its parameters.

Proof:

(1) To prove this theorem, we only need to prove that if the number of values is less than p, then it is 1 or 2.

(2) Assume that the number of values that the function takes is less than p.

(3) Assume further that the number of values is at least 3.

(4) Let's label them V₁, V₂, V₃

(5) Let's define a permutation P₁ as the reordering of V₁ so that it becomes V₂ so that:

Let V₁ = f(x_i1, x_i2, ..., x_in)

Let V₂ = f(x_j1, x_j2, ..., x_jn)

Then P₁ = (x_i1 → x_j1, ..., x_in → x_jn)

(6) Now, we know that P₁ is an order 2 permutation since:

(a) We can view P₁ as sequence of order 2 permutations (see step 5 above)

(b) Each of the permutations is either changing the value or keeping the value. By Corollary 1.2 above, if one of the permutations changes the value, then any order-2 permutation applied to it must undo the change.

(c) So, clearly if the value changes, only of the sequence of order-2 permutations changes the value.

(7) Using the same logic as step #5, we can define a permutation that changes V₂ to V₃ and we can assume that this permutation consists of a sequence of order-2 permutations.

(8) But by the same logic as step #6, P₂ must also be an order-2 permutation.

(9) But now we have a contradiction since if we can apply P₁ to V₁ to change the value to V₂ and we can apply P₂ to V₂ to change the value to V₃, then we have a situation where application of two 2-order permutations results in a change of value which contradicts Corollary 1.2.

(10) Therefore, we must reject our assumption in step #3 and assume that the number of values is at most 2.

QED

References

• Peter Pesic, Abel's Proof: An Essay on the Sources and Meaning of Mathematical Unsolvability, The MIT Press, 2004.