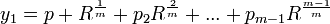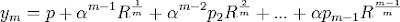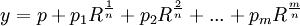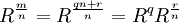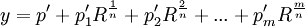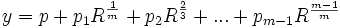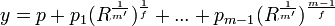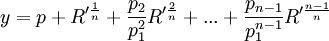Abel's Impossibility Proof: Radicals of the form R(1/m)

In today's blog, I will show an important step in the famous proof by Niels Abel that there is no general solution to the quintic equation expressible in radicals.

In today's blog, I will focus on one result:

If a solution to the general quintic is expressible in nested radicals, then for all radicals of the form R^(1/m), m = 2.

Lemma 1:

Let:

R be a symmetric function on distinct m parameters y₁, ..., y_m

If R^(1/m) is also rational function on these m parameters, then:

it takes m values when the m distinct parameters are permuted.

Proof:

(1) Let R be a symmetric function on m distinct parameters such that:

R(y₁, ..., y_m) = R(y₂, ..., y₁) = ... = R(y_m, ..., y₁)

(2) Let r be a function on y₁, ...., y_m such that r(y₁, ..., y_m) = R(y₁, ..., y_m)^(1/m) such that:

[r(y₁, ..., y_m)]^m = R(y₁, ..., y_m)

(4) By the fundamental theorem of algebra, we know that there are at most m roots that satisfy r^m - R = 0. [See here for proof of the Fundamental Theorem of Algebra]

(5) Since R is the same value for all permutations (since it is symmetric), it follows that r can only take on at most m distinct values in order r^m = R to remain true.

(6) Let α be a primitive mth root of unity.

(7) Then it follows that the possible values of r are r, αr, α²r, ..., α^m-1r.

(8) This means that there are at least m distinct return values and multiplying αⁱ to r is the same as permuting its parameters.

QED

Corollary 1.1

Let R be a rational function on distinct parameters p₁, ..., p_n that takes s distinct return values when these parameters are permuted

Then:

If R^(1/m) is also a function on those n parameters, it follows, that R^(1/m) takes exactly s*m return values when the n parameters are permuted.

Proof:

(1) Let r be a function on y₁, ...., y_m such that r(y₁, ..., y_m) = R(y₁, ..., y_m)^(1/m) such that:

[r(y₁, ..., y_m)]^m = R(y₁, ..., y_m)

(2) By the fundamental theorem of algebra, we know that there are at most m roots that satisfy r^m - R = 0. [See here for proof of the Fundamental Theorem of Algebra]

(3) And, by assumption, there are s different values of R such that we have R₁, ..., R_s

(4) So, it follows that r necessarily has s*m distinct values when its n parameters are permuted since it must satisfy the following s equations which each have m distinct values:

r^m - R₁ = 0

r^m - R₂ = 0

...

r^m - R_s = 0

QED

Lemma 2: The coefficients of a polynomial are symmetric with respect to the roots of the polynomial.

Proof:

(1) From the fundamental theorem of algebra (see here), we know that any polynomial of degree n has n roots and futher that:

a₀xⁿ + ... + a_n-1x + a_n = (x - r₁)(x - r₂)*...*(x - r_n)

where r₁, ..., r_n are the n roots.

(2) From step #1, it is clear that we can view any polynomial as a function of the n roots.

(3) But in this case, it is clear that that permuting the order of the roots will not change the value of the function and hence will not change the value of the coefficients of the polynomial.

QED

Lemma 3:

Let



where R is a function of the m parameters y₁, ..., y_m

Then:

each S, S_i, V^(1/n) are also functions of the m parameters y₁, ..., y_m

Proof:

(1) Let r(x) = S + x + S₂x² + ... + S_n-1x^n-1

(2) Now, it is clear that R = r(V^(1/n))

(3) Let α be a primitive n-th root of unity (such that αⁿ = 1 but α ≠ 1)

(4) We can also define:

R₂ = r(αV^(1/n)) =

= S + αV^(1/n) + S₂α²V^(2/n) + ... + S_n-1α^n-1V^(n-1)/n

...

R_n = r(α^n-1V^(1/n)) =

= S + α^n-1V^(1/n) + S₂α^2(n-1)V^(2/n) + ... + S_n-1α^(n-1)(n-1)V^(n-1)/n

(5) Now, we can use the reasoning in Lemma 2 (see here), Lemma 3 (see here), and Lemma 4 (see here), to conclude that:

S = (1/n)(R + R₂ + ... + R_n)

V^(1/n) = (1/n)(R + α^n-1R₂ + ... + αR_n)

S_iV^(i/n) = (1/n)(R + α^n-iR₂ + ... + αⁱR_n)

(6) Since R, R₂, ..., R_n are all functions of α and y₁, ..., y_m, and since S, V^(1/n), S_i are functions of α, R, R₂, ..., R_n, it follows that S, V^(1/n), S_i are all functions of α and y₁, ..., y_m.

QED

Corollary 3.1:

If a solution to the general mth equation is expressible in the form:



where m is a prime number and R, p₂, ..., p_m-1 are all functions of this same form finitely nested and at the deepest level each p,p_i,R is a function of the coefficients of the general mth equation.

Then:

at all levels, R is a function of the m roots of the the general mth equation

Proof:

(1) At the top level, we know that this is true from Corollary 5.1 here.

(2) Assume it is true up to level i-1 where i-1 ≥ 1 (where 1 = the top level).

(3) But, then using Lemma 3 above, it is true at the level i too.

(4) Therefore, by induction, it is true at all levels of the expression.

QED

Lemma 4:

Let r be a function on m parameters where m is prime and r^m is a symmetric function (that is, it only takes on 1 return value when the m parameters are permuted)

Then:

r can take 1, 2, or m return values when the m parameters are permuted

Proof:

(1) Now, we know that there are m! ways to permute m parameters. [See Lemma 1, here for a review of factorials if needed]

(2) Using Lagrange's Theorem, we know that the number of return values that r takes when the parameters are permuted must divide m!. [See Theorem, here]

(3) From Lemma 1 above, we know that it can take at most m distinct return values.

(4) Using Cauchy's Theorem on Permutations (see Theorem 2, here), we know that r can only take 1, 2, or m different return values when the parameters are permuted.

QED

Lemma 5:

If:

a function v on (y₁, ..., y₅), is symmetric on 4 of the parameters

and the a polynomial y⁵ - ay⁴ + by³ - cy² + dy - e is a quintic equation that takes y₁, ... , y₅ as its roots

Then:

we can assume that there exists functions p,q,r,s such that:

p+y₁ = a

q + py₁ = b

r + qy₁ = c

s + ry₁ = d

and

v is a function on p,q,r,s,y₁

Proof:

(1) Let f be a function on 5 parameters that is symmetric where 4 of the parameters are permuted such that:

f(y₁, y₂, ..., y₅) = f(y₁, y₃, ...) = f(y₁, y₅, ....)

(2) Using the Fundamental Theorem of Algebra (See here for proof of the Fundamental Theorem of Algebra), we know that there exists p,q,r,s such that:

(y - y₂)*...(y - y₅) = y⁴ - py³ + qy² -ry + s.

(3) Since this is a quartic equation and quartic equations are solvable (see Theorem, here), we know that we can define y₂, y₃, y₄, y₅ as functions of p,q,r,s.

(4) Now, from the Fundamental Theorem of Algebra, we also know that there exists a,b,c,d,e such that:

(y - y₁)*...*(y - y₅) = y⁵ - ay⁴ + by³ - cy² + dy - e.

(5) So we have:

(y - y₁)(y⁴ - py³ + qy² -ry + s) = y⁵ - ay⁴ + by³ - cy² + dy - e.

(6) So we can conclude that p,q,r,s can be expressed in terms of a,b,c,d, and y₁ since:

(a) (y - y₁)(y⁴ - py³ + qy² -ry + s)=

y⁵ - (p + y₁)y⁴ + (q + py₁)y³ - (r + qy₁)y² + (s + ry₁)y - sy₁

(b) So that we have:

p+y₁ = a

q + py₁ = b

r + qy₁ = c

s + ry₁ = d

(c) So solving for each above, we get:

p = a - y₁

q = b - py₁ = b - ay₁ + y₁²

r = c - qy₁ = c - by₁ + ay₁² - y₁³

s = d - ry₁ = d - cy₁ + by₁² - ay₁³ + y₁⁴

(7) Since f is a function of y₁, ..., y₅ and y₂, ..., y₅ are functions of p,q,r,s, then it follows that f is a function of y₁, p, q, r, s

QED

Lemma 6:

Let:

R be a rational function of the coefficients of a general quintic equation and also a rational function of the 5 roots of that quintic equation

and

m be a prime number such that R^(1/5) is not a rational function.

Then:

R^(1/5) does not return 5 values when its parameters are permuted.

Proof:

(1) Assume that R^(1/5) is a function on the 5 roots of a quintic equation that returns 5 different values when its parameters are permuted.

(2) Since it returns 5 distinct values, we know that it is not symmetric on all 5 parameters.

(3) On the other hand, it must be symmetric on at least 4, otherwise, it would return more than 5 return values (it would return at least 5*4 = 20 return values)

(4) So, we can conclude that it is symmetric on four and the parameters which can label y₂, ..., y₅ and we label the other parameter y₁.

(5) From Lemma 5 above, we know that there exists p,q,r,s which are functions of the coefficients of the quintic equation such that:

R^(1/5) is a function of p,q,r,s,y₁

(6) Therefore, there exists p, p₁, ..., p_n where each is a function of the coefficients of the quintic equation such that:

R^(1/5) = p₀ + p₁y₁ + p₂ + y₁² + ... + p_ny₁ⁿ

(7) Now, we can also assume that n ≤ 4 since:

(a) Each root is a solution to the quintic equation and we can assume that:

y₁⁵ - ay₁⁴ + by₁³ - cy₁² + dy₁ - e =0

(b) Then:

y₁⁵ = ay₁⁴ - by₁³ + cy₁² - dy₁ + e

(8) So, we have:

R^(1/5) = p₀ + p₁y₁ + p₂ y₁² + ... + p₄y₁⁴

(9) Now, we know that the 5 values that R^(1/5) can take on are:

R^(1/5), αR^(1/5), ..., α⁴R^(1/5)

(10) So, let's assume that switching y₁, y₂ results in R^(1/m) taking on the value α⁴R^(1/5)

(11) Now, this gives us that:

α⁴R^(1/5) = p₀ + p₁y₂ + p₂y₂² + ... + p₄y₂⁴

(12) So, multiplying each side by α gives us:

R^(1/5) = αp₀ + αp₁y₂ + αp₂y₂² + ... + αp₄y₂⁴

(13) But then combining step #8 with step #12, we get:

p₀ + p₁y₁ + p₂ y₁² + ... + p₄y₁⁴ = αp₀ + αp₁y₂ + αp₂y₂² + ... + αp₄y₂⁴

(14) But this is impossible unless y₁ = y₂ or α = 1.

(15) But α is a primitive 5th root of unity so α ≠ 1.

(16) Further, y₁ ≠ y₂ since we assume that swapping these two parameters resulted in a change of value from R^(1/m) to α⁴R^(1/m)

(17) So, we have a contradiction and we are forced to reject our assumption in step #1.

QED

Corollary 6.1:

Let r be a function on m parameters where m is prime and r^m is a symmetric function (that is, it only takes 1 return value when the m parameters are permuted)

Then:

m = 2

Proof:

(1) By Lemma 4 above, the function r can take 1, 2, or m return values.

(2) Since by assumption, m is prime and m divides 5! (See Lagrange Theorem, here for details] it follows that m = 2 or 5.

(4) From Lemma 6 above, we know that m cannot return 5 distinct values so m returns 1 or 2 distinct values when its parameters are permuted.

(5) Since its parameters are distinct, it follows that R^(1/m) must return 2 different values when its parameters are permuted.

(6) Assume that m = 5.

(7) Then we have a contradiction from Lemma 1 since that imples that R^(1/5) would take on 5 distinct return values which is impossible.

(8) So reject our assumption in step #6 and conclude that m = 2.

QED

References

• Peter Pesic, Abel's Proof: An Essay on the Sources and Meaning of Mathematical Unsolvability, Appendix B, The MIT Press, 2004

Abel's Proof: Step Two

In today's blog, I will cover step 2 of the original proof by Niels Abel on the quintic equation. The content in today's blog is taken from Peter Pesic's excellent book Abel's Proof.

In Step 2, Abel shows that if the general quintic equation has a solution expressible in radicals, then all irrational functions in this formula are expressible as rational functions of the roots.

This step was the gap in Paolo Ruffini's proof.

Lemma 1:

The equation:

[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁵ -a[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁴ + ... + e = 0

can be reduced to:

0 = q + q₁R^(1/m) + q₂(R^(2/m)) + ... + q_m-1R^(m-1)/m

where q, q₁, q₂, ... are rational functions based on the quantities a,b,c,d,e,p,p₂, ... and R.

Proof:

(1) We start with the following:

[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁵ -
a[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁴ + ... + e = 0

where a,b,c,d,e are rational coefficients.

(2) Since the equation does not involve any additional radicals, we can see that it can be ordered around sums of xR^(u/m) where x is a rational function of p,R,a,b,c,d,e and u is an integer.

(3) If u is greater m, then there exists q,r such that u=qm + r where r ≤ m-1.

(4) xR^(u/m) = xR^(qm+r)/m = xR^q*R^(r/m)

(5) If we set x' = x*R^q, then we have:

xR^(u/m)=x'R^(r/m) where r is less than m.

(6) So, if we number each of the x', then we are left with:

[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁵ - a[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁴ + ... + e =x'₀R^(0/m) + x'₁R^(1/m) + ... + x'_m-1R^(m-1)/m

where x_i is a rational function of a,b,c,d,e,p,p_i,R

QED

Corollary 1.1:

If R^1/m is not expressible in rationals, then q, q₁, q₂, ... all = 0.

Proof:

(1) Let z = R^(1/m)

(2) So, we have two equations:

z^m - R = 0

and

q + q₁z + ... + q_m-1z^m-1 = 0

(3) Using Abel's Lemma (see Lemma 2, here), we can conclude that z^m - R=0 is not reducible in rationals.

(4) Now, since R^(1/m) is a root for both equations, we can use Abel's Irreducibility Theorem (See Thereom 3 here) to conclude that q, q₁, ..., q_m-1 must all equal 0.

QED

Lemma 2:

If:





...



Then:

p = (1/m)(y₁ + y₂ + ... + y_m)

Proof:

(1) y₁ + y₂ + ... + y_m =

mp + (1 + α + α² + ... + α^m-1)R^(1/m) + p₂(1 + α + α² + ... + α^m-1)R^(2/m) + ... + p_m-1(1 + α + α² + ... + α^m-1)R^(m-1)/m

(2) Since (1 + α + α² + ... + α^m-1)=0 (see Lemma 2, here), we are left with:

mp = y₁ + y₂ + ... + y_m

(3) So that we have:

p = (1/m)(y₁ + y₂ + ... + y_m)

QED

Lemma 3:

If:





...



Then:

R^(1/m) = (1/m)(y₁ + α^m-1y₂ + ... + αy_m)

Proof:

(1) y₁ + α^m-1y₂ + α^m-2y₃ + ... + αy_m =

= (1 + α + α² + ... + α^m-1)p + mα^mR^(1/m) + p₂α^m(1 + α + α² + ... + α^m-1)R^(2/m) + .... + α^mp_m-1(1 + α + α² + ... + α^m-1)R^(m-1)/m

(2) Since α^m = 1 and (1 + α + α² + ... + α^m-1)=0 (see Lemma 2, here), we are left with:

mR^(1/m) = y₁ + α^m-1y₂ + α^m-2y₃ + ... + αy_m

QED

Lemma 4:

If:





...



Then:

p_iR^(i/m) = (1/m)(y₁ + α^m-iy₂ + ... + αⁱy_m)

Proof:

(1) For any i, we have:

y₁ + α^m-iy₂ + ... + αⁱy_m =

= (1 + α + α² + ... + α^m-1)p + mα^m(1 + α + α² + ... + α^m-1)R^(1/m) + ... + p_iα^mR^(i/m) + .... + α^mp_m-1(1 + α + α² + ... + α^m-1)R^(m-1)/m

(2) Since α^m = 1 and (1 + α + α² + ... + α^m-1)=0 (see Lemma 2, here), we are left with:

mp_iR^(i/m) = y₁ + α^m-iy₂ + α^m-(i+1)y₃ + ... + αⁱy_m

QED

Theorem 5:

Let :



be a solution to the general quintic equation:

y⁵ - ay⁴ + by³ - cy² + dy - e =0

where p,p₂,..., p_m-1, R are expressible in radicals, m is a prime, and R^(1/m) is irrational.

Then the m roots are:





...



Proof:

(1) We can represent the general quintic equation as follows:

y⁵ + ay⁴ + by³ + cy² + dy - e = 0

(2) If we now insert this solution into the equation at step #1, we are left with:

[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁵ -
a[p + R^(1/m) + ... + p_m-1R^(m-1)/m]⁴ + ... + e = 0

(3) Using Lemma 1 above, we can reduce the above result to get:

0 = q₀ + q₁R^(1/m) + q₂R^(2/m) + ... + q_m-1R^(m-1)/m

where q₀, q₁, q₂, ... are rational functions based on the quantities a,b,c,d,e,p,p₂, ... and R.

(4) Using Corollary 1.1 above, we know that:

q₀, q₁, ..., q_m-1 all equal 0.

(5) Now, it is also clear that R^(1/m) has m different solutions where if R^(1/m) is one solution, the solutions are:

R, αR, α²R,..., α^m-1R where α is a m-th root of unity.

(6) So, if we use our equation for y, we are left with m roots:





...



QED

Corollary 5.1:

Let :



be a solution to the general quintic equation:

y⁵ - ay⁴ + by³ - cy² + dy - e =0

where p,p₂,..., p_m-1, R are expressible in radicals, m is a prime, and R^(1/m) is irrational.

Then:

p,p₂, ..., p_m-1, R^(1/m) are rational functions of α, and the roots: y₁, y₂, ..., y₅

Proof:

(1) From Theorem 5 above, we have the m roots as:





...



(2) Now, we complete this proof using Lemma 2, Lemma 3, and Lemma 4, since now we have:

p = (1/m)(y₁ + y₂ + ... + y_m)

R^(1/m) = (1/m)(y₁ + α^m-1y₂ + ... + αy_m)

p_iR^(i/m) = (1/m)(y₁ + α^m-iy₂ + ... + αⁱy_m)

QED

Corollary 5.2:

Let :



be a solution to the general quintic equation:

y⁵ - ay⁴ + by³ - cy² + dy - e =0

where each R is itself expressible in the same form such as:



Then:

there exists t, t_1,1, ... t_5,4 such that:

v^(1/n) = t + t_1,1y₁ + ... + t_1,4y₁⁴ + ... + t_5,1y₅ + ... + t_5,4y₅⁴

where v is any nested element of the above form.

Proof:

(1) If v is at the top level, then from Corollary 5.1 above, we know that:

v^(1/m) = (1/m)(y₁ + α^m-1y₂ + ... + αy_m)

(2) Likewise, if v is at the first nested level with R at the top level, then:



(3) Using the same logic as Corollary 5.1 above, we where treat R₁ = R, R₂ = αR, ..., R₅ = α⁴R, then we have:

v^(1/n) = (1/n)(R₁ + α^n-1R₂ + ... + αR_n)

(4) Then substituting the equation in step #1 above gives us:

v^(1/n) = (1/n)({(1/m)[y₁ + ... + αy_m]}⁵ + ... + α*α⁴{(1/m)[y₁ + ... + αy_m]}⁵)

(5) We can keep doing this substitution as far as needed so that we can assume that any nested form of v^(1/n) is a function of y₁, y₂, ..., y₅

(6) Finally, we can assume that no power is greater than m-1 since each root is a solution to the quintic equation and we can assume that:

y_i⁵ - ay_i⁴ + by_i³ - cy_i² + dy_i - e =0

(7) And further that:

y_i⁵ = ay_i⁴ - by_i³ + cy_i² - dy_i + e

QED

References

• Peter Pesic, Abel's Proof: An Essay on the Sources and Meaning of Mathematical Unsolvability, Appendix B, The MIT Press, 2004

Abel's Lemmas on Irreducibility

In today's blog, I present a few lemmas that Niels Abel published on irreducibility. These lemmas are used in Abel's proof on the insolvability of the quintic equation.

The content in today's blog is taken from 100 Great Problems of Elementary Mathematics by Heinrich Dorrie.

Definition 1: expressible in rationals

"A number or equation is expressible in rationals if it is expressible using only addition, subtraction, multiplication, and division of integers."

Definition 2: rational functions

A function f(x) is rational if its coefficients are all rational numbers.

Definition 3: degree of a polynomial

The degree of a polynomial is the highest power of the polynomial that has nonzero coefficients.

Definition 4: reducible over rationals

A function f(x) with coefficients in the rational numbers is said to be reducible over rationals if it can be divided into a product of polynomials with lower degree and rational coefficients.

Definition 5: free term or constant term of a polynomial

The free term or constant term of a polynomial is the value that is not bound to an unknown.

Lemma 1: The free term is equal to the product of roots.

Proof:

(1) Let a₀xⁿ + a₁x^n-1 + ... + a_n-1x + a_n be an n degree polynomial.

(2) By the Fundamental Theorem of Algebra (see Theorem, here), we know that there are n roots such that:

a₀xⁿ + a₁x^n-1 + ... + a_n-1x + a_n = (x - r₁)*(x - r₂)*...*(x - r_n)

(3) Now, it is clear that of the products in step #2, the only term that does not include x is the product of all the roots.

QED

Lemma 2: Abel's Lemma

The equation x^p = C where p is a prime number is irreducible over rationals when C is a rational number not the pth power of a rational number

Proof:

(1) Assume that x^p = C is reducible into rational functions.

(2) Then, there exists f(x),g(x) such that x^p - C = f(x)g(x) where f(x),g(x) are rational functions of lower degree.

(3) We know that the roots to x^p - C=0 are r, rα, rα², ... rα^p-1 where r is one of the roots and α is a pth root of unity since:

(rαⁱ)^p = (r^p)(αⁱ)^p = (r^p)(α^p)ⁱ = r^p*(1)ⁱ = r^p

(4) Let A,B be the the free terms for f(x) and g(x) respectively.

(5) Since a free term is the product of a function's root (see Lemma 1 above), we know that A*B = (r)*(rα)*(rα²)*...*(rα^p-1) = ± C

(6) We can see that C = r^p since:

(a) If p=2, then α=-1 and the roots are r*(-r) = -r²

(b) If p is a prime ≥ 3, then using the summation formula (see Corollary 2.1, here), we have:

C = r^pα^{[(1/2)(p)(p-1)]}

(c) Since p-1 is even, we have:

C = r^p(α^p)^(1/2)(p-1) = r^p(1)^(1/2)(p-1) = r^p

(7) Likewise, there exists μ, M, ν, N such that:

A = r^μα^M

B = r^να^N

(8) Since there are p instances of r in the product in step #5, we know that:

μ + ν = p

(9) We further know that gcd(μ,ν) = 1 since:

(a) Assume that gcd(μ,ν) = f which is greater than 1.

(b) So μ = mf and ν = nf

(c) Then p = mf + nf = f(m+n)

(d) But p is prime so this is impossible and f=1.

(10) Using Bezout's Identity (see Lemma 1, here), we know that there exists h,k such that:

μh + νk = 1

(11) Now let's define a rational number K as K = A^h*B^k

(12) So that K= A^h*B^k = r^hμα^M*r^kνα^N = r^{(hμ + kν)}α^hM+kN = rα^hM+kN

(13) But then K^p = (rα^hM+kN)^p = r^p*(α^p)^hM+kN = r^p

(14) But this is impossible since we selected an integer C that is not a p-th power.

QED

Theorem 3: Abel's Irreducibility Theorem

Let f(x) be irreducible over rationals.

If one root of the equation f(x) is also a root of the rational equation F(x)=0

Then:

All the roots of f(x) are roots of F(x) and F(x) can be divided by f(x) without a remainder.

Proof:

(1) Using Euclid's Greatest Common Divisor Algorithm for Polynomials (see Theorem 3, here), we are left with:

V(x)F(x) + v(x)f(x) = g(x)

(2) If F(x) and f(x) have no common divisor, then g(x) is a constant. That is, g(x) = g₀ where g₀ is the free term.

(3) If f(x) is irreducible and a root r of f = 0 is also a root of F(x), then there exists a common divisor of at least the first degree (x-r)

(4) Since f(x) is irreducible, f₁(x) must equal a constant and f(x)=g(x)*f₁(x) = g(x)*f1₀.

(5) Then, F(x)=F₁(x)*g(x) = F₁(x)*f(x)*f1₀

(6) Thus, F(x) is divisible by f(x) and vanishes for every zero point of f(x).

QED

Corollary 3.1:

If a root of an equation f(x)=0 which is irreducible in rational numbers is also a root of F(x)=0 in rational numbers of lower degree than f, then all the coefficients of F are equal to zero.

Proof:

(1) Assume that at least one coefficient of F is not zero.

(2) Then F is a polynomial with a degree of at least 1.

(3) Since there is a root that divides both f(x) and F(x) and since f(x) is irreducible over rationals, we can use Theorem 3 above to conclude that every root of f(x) divides F(x).

(4) But F(x) has a lower degree than f(x) which is impossible.

(5) So we reject our assumption at step #1 and conclude that all coefficients of F must be 0.

QED

Corollary 3.2:

If f(x)=0 is an irreducible over rationals, then there is no other equation irreducible over rationals that has a common root with f(x)=0.

Proof:

(1) Let f(x) and g(x) be functions irreducible over rationals.

(2) Assume that f(x) and g(x) have a common root r.

(3) Then we can use Theorem 3 above to conclude that f(x) divides g(x) and g(x) divides f(x).

(4) But if f(x) divides g(x) and g(x) divides f(x), it is clear that f(x) = g(x).

QED

References

• 100 Great Problems of Elementary Mathematics (Dover, 1965)

Abel's Form of a General Solution by Radicals

The first step in Niel Abel's 1824 proof on the insolvability of the general quintic equation is the statement that if a general solution to the quintic exists, it can be assumed to have the following form:



where m is a prime number and R, p₂, ..., p_m-1 are all functions of this same form finitely nested and are functions of the coefficients of the general quintic equation.

Today's content is taken from Peter Pesic's Abel's Proof.

Lemma 1:

If a mathematical expression is expressible by radicals, then it is stateable in the form:

(A₁ + A₂ + ... + A_m)/(B₁ + B₂ + ... + B_n) where each A_i, B_i are expressible by radicals.

Proof:

(1) First, I show that if a mathematical expression is minimally expressible by radicals, then it is expressible by the desired form:

a + b = (a + b)/(1)

a - b = (a - b)/(1)

a * b = (a*b)/(1)

a/b = (a)/(b)

√a = (a^(1/2))/(1)

(2) By the above analysis, we know that it works to at least the minimum number of operations. Let's assume that it works only up to n operations.

(3) To complete the proof, I will show that I can add an additional operation to the above form and maintain the above form. I only need to show that this is true for addition, subtraction, multiplication, division, and radicals:

(±)a + (A₁ + ... + A_m)/(B₁ + ... + B_n) =

= (A₁ + ... + A_m + (±)a[B₁ + ... + B_n])/(B₁ + ... + B_n)

a*(A₁ + ... + A_m)/(B₁ + ... + B_n) =

= (a*A₁ + ... + a*A_m)/(B₁ + ... + B_n)

(1/a)*(A₁ + ... + A_m)/(B₁ + ... + B_n) =

= (A₁ + ... + A_m)/(a*B₁ + ... + a*B_n)

[ (A₁ + ... + A_m)/(B₁ + ... + B_n)]^(1/a) = [(A₁ + ... + A_m)]^(1/a)/[(B₁ + ... + B_n)^(1/a)]


QED

Lemma 2:

If the general quintic equation has a solution which has the form:

y = (A₁)^(c₁/d₁) + (A₂)^(c₂/d₂) + ... + (A_n)^(c_n/d_n)

where each A_i is expressible by radicals

then it can be put into the following form:



where R, p₁, ..., p_m-1 are all functions of this same form finitely nested.

Proof:

(1) By assumption, we can state the solution to the general quintic equation in the following form:

y = (A₁)^(c₁/d₁) + (A₂)^(c₂/d₂) + ... + (A_n)^(c_n/d_n)

where each A_i are expressible as radicals.

(2) Now, if we set each A'_i to (A_i^c_i), then we get:

y = (A'₁)^(1/d₁) + (A'₂)^(1/d₂) + ... + (A'_n)^(1/d_n)

(3) Since, the expression has finite complexity, it follows that there can only be a finite number of expressions of the form (A'_i)^(1/d_i)

(4) So, there exists a number k such that:

[number of radicals in y] = k.

(5) Now, we can put this expression in the desired form by setting:

R = A'₁

m = d₁

p₁ = 1

p = (A'₂)^(1/d₂) + ... + (A'_n)^(1/d_n)

p_i = 0 where i ≠ 1.

(6) This changes y into

y = p + p₁R^(1/m)

(7) Now, it is clear that:

[number of radicals in p] + [number of radicals in R] = [number of radicals in y] - 1 = k-1

(8) And since we do the same refactoring for all in radicals in p and all radicals in R and since there are only a finite amount of them, we can put all radicals into the desired form.

(9) To complete the proof, we need only show that an equation without radicals can also be put into this form.

(10) So assume y does not have radicals. That is:

[number of radicals in y] = 0

(13) Then let:

p = A₁^c₁ + A₂^c₂ + ... + A_n^c_n

with each p_i=0.

QED

Corollary 2.1:

If the general quintic equation has a solution, then it can be put into the following form:



where R, p₁, ..., p_m-1 are all functions of this same form finitely nested.

Proof:

(1) Using Lemma 1 above, if the solution to the general equation is expressible by radicals, then it follows that y is expressible as:

y = (A₁ + A₂ + ... + A_m)/(B₁ + B₂ + ... + B_n) where each A_i, B_i are expressible by radicals.

(2) Let:

T = A₁ + A₂ + ... + A_m

W = B₁ + B₂ + ... + B_n

such that we have:

y = T/W

(3) Using Lemma 2 above, we know that T,W can be put in the following forms:





(4) Let:

W(x) = w₀ + w₁x + w₂x² + ... + w_vx^v

α = an n-th root of unity. (that is, α ≠ 1 and αⁿ=1)

(5) So, we now define W₀, W₁, ..., W_n-1 with:

W₀ = W(R^(1/n)) = W

W₁ = W(αR^(1/n))

W₂ = W(α²R^(1/n))

...

W_n-1 = W(α^n-1R^(1/n))

(6) So, if we multiply (W₁*...*W_n-1)/(W₁*...*W_n-1), we get:

Y = (T*W₁*...*W_v-1)/(W*W₁*...*W_v-1)

(7) Multiplying W*W₁*...*W_n-1 out, we get:

W*W₁*W₂*...*W_n-1 =

= (w₀ + w₁R^(1/n) + w₂R^(2/n) + ... + w_vR^(v/n))*(w₀ + αw₁R^(1/n) + α²w₂R^(2/n) + ... + α^vw_vR^(v/n))*(w₀ + α²w₁R^(1/n) + α⁴w₂R^(2/n) + ... + α^2vw_vR^(v/n))*...*(w₀ + α^(n-1)w₁R^(1/n) + α^2(n-1)w₂R^(2/n) + ... + α^v(n-1)w_vR^(v/n)) =

=w₀ⁿ + αw₀^n-1w₁(1 + α + α² + ... + α^n-1) + ... α²w₀^n-2w₂R^(2/n)(1 + α + α² + ... + α^n-1) + ...

(8) Now, since (1 + α + α² + ... + α^n-1) = 0 [See Lemma 2, here], we have:

W*W₁*W₂*...*W_n-1 = v₀ⁿ

(9) If w₀ⁿ contains radicals, then we set W=w₀ⁿ and we repeat the process.

(10) Since the original W has only a finite nesting of radicals, it follows that eventually we will reach a w₀ⁿ that does not contain any radicals and we set each of the resulting t_i = t_i/(w₀ⁿ)

QED

Lemma 3:

For the following expression



We can assume that m is less than n.

Proof:

(1) Assume that m is not less than n.

(2) Then, we there exists q,r such that (see Theorem 1, here):

m = qn + r

where q ≥ 1, and 0 ≤ r ≤ n-1

(3) Then:



(4) Now, if we define p'_i so that:

p'_i = p_i*R^q, then we are left with:



where m is less than n.

QED

Lemma 4:

For any equation of the following form:



We can assume that m is prime.

Proof:

(1) Assume that m is not prime.

(2) Then m consists of a finite number of primes. [See Theorem 3, here for proof of the Fundamental Theorem of Arithmetic]

(3) Let's take out the first prime which I will call f. So that we have m = f*m'.

(4) So we can restate y as:



(5) Now, we can redefine each R such that:

R = R^(1/m')

(6) After this, we are left with an equation of the desired form.

QED

Theorem 5: Abel's General Form

If a general solution to the quintic exists, it can be assumed to have the following form:



where m is a prime number and R, p₁, ..., p_m-1 are all functions of this same form finitely nested and are functions of the coefficients of the general quintic equation.

Proof:

(1) By Corollary 2.1 above:

If the general quintic equation has a solution, then it can be put into the following form:



where R, p₁, ..., p_m-1 are all functions of this same form finitely nested.

(2) By Lemma 3 above, we can assume that m is less than n.

(3) By Lemma 4 above, we can assume that n is prime.

(4) Let R' = R/[p₁ⁿ]

(5) Then we have:


(6) Now, for all this nesting of equations of this form, at the end, each R' must be in a function of the coefficients of the general quintic equation.

(7) If not, then it does not represent a solution to the general quintic since a solution consists of determining each of the roots based on the coefficients given.

QED

References

• Peter Pesic, Abel's Proof: An Essay on the Sources and Meaning of Mathematical Unsolvability, Appendix B, The MIT Press, 2004.