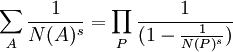
where A ranges over the set of ideal numbers, P ranges over the set of prime divisors of ideal numbers, and N(X) is the norm for these ideal numbers [for review of ideal numbers, start here] and s is greater than 1.
The content in today's blog is taken from Harold M. Edwards' Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory.
Theorem 1: For s greater than 1, ∏ (1 - N(P)-s)-1 converges absolutely
Proof:
(1) Let λ be a prime number such that αλ = 1 for any positive integer i less than λ, αi ≠ 1. [See here for review of cyclotomic integers and λ]
(2) N(P) = pf where p is a prime divisible by the prime divisor P and f is the exponent of p mod λ (or f=1 if p = λ) [See Lemma 1, here for proof N(P)=pf or here for f=1 if p=λ]
(3) N(P)-s = p-fs ≤ p-s
(4) Let e = (λ - 1)/f [See Lemma 1, here for proof that f divides λ-1] so that e ≤ λ - 1.
(5) We know from a previous result (see Lemma 1, here), that there are e prime divisors for a given prime p so that we know that:
∑ N(P) for a given P ≤ (λ - 1)∑ pf
(6) So that:
∑ N(P)-s ≤ (λ - 1) ∑ p-fs which is less than (λ - 1)∑ p-s which is less than (λ - 1)∑ n-s
(7) From a previous result (see Theorem 1, here), we know that ∑ n-s converges if s is greater than 1 so, we can conclude that ∑ N(P)-s necessarily converges.
(8) Since N(P)=pf is greater than 0, it follows that ∑ N(P)-s = ∑ abs(N(P)-s) and using Lemma 3, here, we can conclude that:
∏ (1 - abs(N(P)-s)) converges
(9) This gives us (see Definition 1, here) that ∏ (1 - N(P)-s) converges absolutely.
(10) Using the Reciprocal Law (see Lemma 6, here), we conclude that ∏ (1 - N(P)-s)-1 also converges absolutely.
QED
Lemma 2: For s greater than 1, ∑ N(A)-s ≤ ∏ (1 - N(P)-s)-1
Proof:
(1) Let A* be any set of A and S* be defined such that S* = ∑ (A ∈ A*) N(A)-s
(2) Let P* be the set of prime divisors that make up any of the A in A*. [See here for a review of prime divisors of an ideal number]
(3) For each P ∈ P*, we see that (1 - N(P)-s)-1 = 1 + N(P)-s + N(P2)-s + N(P3)-s + .... [ See Lemma 1, here]
(4) It is then clear that ∏ (1 - N(P)-s)-1 = the product of all of these geometric series which includes all A in A*.
(5) Since N(Pi) -s continues ad infinitum, there also necessarily exists N(Pi)-s that is not a divisor of any N(A) where A ∈ A* since A* is a finite set by assumption.
(6) So, any partial sum is less than the partial product.
(7) In this way, we can conclude that the infinite sum ∑ N(A) ≤ the infinite product ∏ (1 - N(P)-s)-1
QED
Corollary 2.1: ∑ N(A)-s converges absolutely.
Proof:
(1) By Lemma 2 above, ∑ N(A)-s ≤ ∏ (1 - N(P)-s)-1.
(2) Since ∏ (1 - N(P)-s)-1 converges (see Theorem 1 above), then ∑ N(A)-s necessarily converges too.
(3) Since all values N(A)-s are positive, it follows that ∑ N(A)-s converges absolutely. (see Definition 2, here)
QED
Theorem 3: ∑ N(A)-s = ∏ (1 - N(P)-s)-1
Proof:
(1) By Lemma 2 above, we have:
∑ N(A)-s ≤ ∏ (1 - N(P)-s)-1
(2) Let P* be the same set of prime divisors from Lemma 2 above.
(3) It is clear that ∏ (1 - N(P)-s)-1 includes as a sum a distinct set of ideal numbers but it does not include all ideal numbers since P* is a finite of P and there are an infinite number of primes p [See Theorem, here].
(4) Let A* be all the set of ideal numbers in the sum ∏ (1 - N(P)-s)-1 plus an ideal number A+ that is divisible by a prime divisor P that is not found in P*.
(5) It is clear that ∑ (A ∈ A*) N(A)-s) ≥ ∏ (P ∈ P*) (1 - N(P)-s)-1
(6) Combining step #5 with step #1 gives us that:
∑ N(A)-s = ∏ (1 - N(P)-s)-1
QED
References
- Harold M. Edwards, Fermat's Last Theorem: A Genetic Introduction, Springer, 2000.

No comments:
Post a Comment