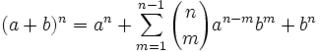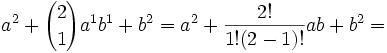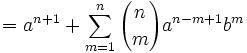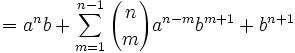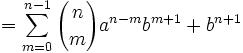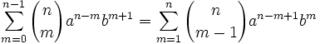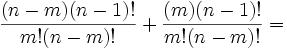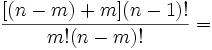Fermat's Last Theorem: n=5: 5 divides z

For those interested in the history behind this proof, you may want to start here.

For those who would like to start at the beginning of this proof, start here.

The proof presented is based on two books: Harold M. Edward's Fermat's Last Theorem: A Genetic Introduction and Paulo Ribenboim's Fermat's Last Theorem for Amateurs.

Lemma: There are no integers x,y,z such that x⁵ + y⁵ = z⁵, xyz ≠ 0, gcd(x,y,z)=1, x,y are odd, z is even, and 5 divides z.

(1) Assume that x,y,z exist.

(2) We know that there exists m,n,z' such that:
z = 2^m5ⁿz' with m ≥ 1, n ≥ 1, [Since 5 divides z and z is even]
gcd(z',2)=1, gcd(z',5)=1. [Since we can make m and n high enough to cover all 2's and 5's]
and 2^5m5⁵ⁿz'⁵ = x⁵ + y⁵ [Since z=2^m5ⁿz', z⁵ = 2^5m5⁵ⁿz'⁵]

(3) There exist two integers p,q that have the following properties:

gcd(p,q)=1
p,q have different parities (one is odd, one is even)
2^5m5⁵ⁿz'⁵ = 2p(p⁴ + 10p²q² + 5q⁴)
p,q ≠ 0

since:

(a) x,y are odd → x+y is even, x - y is even

Since odd + odd = even and odd - odd = even.

[We know that x,y are odd since gcd(x,y,z)=1 and z is even]

(b) From this, we know that there are two values p,q such that:
x + y = 2p
x - y = 2q

(c) We also know that gcd(p,q)=1 since:

x = (1/2)[x + y + x - y] = (1/2)(2x) = (1/2)[2p + 2q] = p + q
y = (1/2)[x + y - (x - y)] = (1/2)(2y) = (1/2)[2p - 2q] = p - q

If there exists a value d greater than 1 that divides both p,q then, from above, it would divide both x,y which is impossible since gcd(x,y)=1 from step (#1).

(d) From step 3(c) above, we can conclude that p,q have different parities (that is, one is odd and the other is even).

p,q can't both have even parity because then x would be even by step 3(c) above since even + even = even but x is odd by step 3(a) above.

p,q can't both have odd parity for the same reason since odd + odd = even.

Therefore, p,q must have different parities where one is odd and one is even since odd + even = odd.

(e) Applying p,q to step (#2) above gives us:

2^5m5⁵ⁿz'⁵ = x⁵ + y⁵ = (p+q)⁵ + (p-q)⁵ = 2p(p⁴ + 10p²q² + 5q⁴) [See Lemma 1, here]

(f) p,q ≠ 0 since gcd(x,y)=1. [If x+y=0 or (x-y)=0, then x=y or x=-y which is not possible.]

(4) There exists an integer r that has these properties:

p=5r
gcd(q,r)=1
q,r have different parities (one is odd, one is even)
2^5m5⁵ⁿz'⁵ = 2*5²r(q⁴ + 50q² r² + 125r⁴)
5 divides r
r ≠ 0

since:

(a) 5 divides p since:

From step (#3e) and Euclid's Generalized Lemma, 5 divides 2p or 5 divides p⁴ + 10p²q² + 5q⁴. If it divides 2p, then it divides p. Likewise, if 5 divides p⁴ + 10p²q² + 5q⁴ then it must also divide p. [Details if needed are here] Either way, it divides p.

(b) From (a), we know that there must exist r such that:
p = 5r

(c) gcd(r,q)=1 since gcd(p,q)=1 from step (#3c).

(d) We know r,q have different parities since r has the same parity as p since:

odd divided by 5 = odd
even divided by 5 = even

p,q have different parities (from step #3d)

(e) Finally, we note that applying r to step #3e gives us:
2p(p⁴ + 10p²q² + 5q⁴)=
2(5r)[(5r)⁴ + 10(5r)²q² + 5q⁴] =
2*5r*5(125r⁴ + 50r²q² + q⁴) =
2*5²r(q⁴ + 50q² r² + 125r⁴)

(f) 5 divides r since:

We know that 5⁵ⁿ divides 2 * 5²r(q⁴ + 50q²r² + 125r⁴) from step (#3e and #4e).

So that 5^5n-2 divides 2 * r(q⁴ + 50q²r² + 125r⁴)

Since n ≥ 1 (step #2 above), 5n ≥ 5 which means 5n is greater than 2 so that we know that:
5 divides 2 * r(q⁴ + 50q²r² + 125r⁴)

Now, we know that 5 doesn't divide q (since 5 divides p and gcd(p,q)=1 ) so that 5 cannot divide q⁴ + 50q²r² + 125r⁴.

By Euclid's Generalized Lemma, since 5 divides 2 * r, it must divide r.

(g) r ≠ 0 since p ≠ 0 from step #3f.

(5) We define three values a,b,t to be the following:

(a) Let t = q⁴ + 50q² r² + 125r⁴

(b) Let a = q² + 25r²

(c) Let b = 10r²

(d) And we note that t = a² - 5b². [By Lemma 2, here]

(6) Now, we note that a,b have the following properties:

(a) gcd(a,b)=1 since:

Assume gcd(a,b) is greater than 1.

Then, there is a prime f that divides both a and b.

Since f divides a, we know that f divides 10r² which by Euclid's Generalized Lemma, gives us three possible cases:

Case I: f divides 2 (in this case, f = 2)
Case II: f divides 5 (in this case, f = 5)
Case III: f divides r (since f divides r² implies f divides r or f divides r.)

Case I is false: because a is odd. a must be odd because q,r have different parities (step #4d) and since (odd)² + 25(even)² = odd + even = odd and (even)² + 25(odd)² = even + odd = odd.

Case II is false: f can't be 5 since 5 divides p and gcd(p,q)=1. This means 5 doesn't divide q and therefore 5 doesn't divide q² + 25r².

Case III is false: If f divides r and f divides a, then f would divide q (since a= q² + 25r² and see here) but this cannot be the case since gcd(r,q)=1.

Since all cases are false, no such prime can exist.

(b) 5 doesn't divide a, 5 divides b

From step #5c we know that 5 divides b. From (a), we know that gcd(a,b)=1 so 5 can't divide a.

(c) a,b have different parities

b is even from #5c so that 2 divides b. But 2 cannot divide a since gcd(a,b)=1.

(d) gcd(2*5²r,t) = 1 since:

Assume there exists a prime f that divides both 2*5²r and t.

We know that f ≠ 2 since t is odd since:

t = (q² + 25r²)² - 5(10r²)².
q,r have different parity (#4d)

Case I: q is odd, r is even
(odd² + 25(even)²)² - 5(10(even)²)² = (odd + 25(even))² - 5(even)² =
= (odd + even)² - even = odd² - even = odd
So, if q is odd, r is even, then t is odd.

Case II: q is even, r is odd
(even² + 25(odd)²)² - 5(10(odd)²)² = (even + odd)² - 5(even)² =
odd² - even = odd.
So, if q is even, r is odd, then t is odd.

Either way, t is odd.

We know that f ≠ 5 since t is not divisible by 5 since 5 doesn't divide q (#6a) [Additional details if needed are here]

Finally, f cannot divide r since gcd(r,t)=1 since:

Assume there exists a prime p' that divides both t,r
p' would then divide q [Additional details if needed are here]
But this is impossible since gcd(q,r)=1 from (#4c).

Therefore, the prime p' doesn't exist and we can conclude that f does not divide r.

(e) t=a - 5b² is a fifth power since:

Since z⁵ = (2*5²r)*(t) from step (#4e) above and since (2*5²r) and (t) are relatively prime from step (# 6d) above, we can conclude that:
t is a fifth power and (2*5²r) is a fifth power [From Relatively Prime Divisors of n-powers]

(f) a,b are positive integers

We know this since q,r are nonzero integers (#3f,#4g) and #5 (since the square of a nonzero integer is a positive integer).

(7) With the properties in step #6, we can use a lemma (see Lemma 1, here):

There exists two integers c,d such that:

a = c(c⁴ + 50c²d² + 125d⁴)
b = 5d(c⁴ + 10c²d² + 5d⁴)
gcd(c,d)=1
c,d have different parities
5 doesn't divide c
5 divides d
c,d are nonzero

(8) Let u' = c + 5d², v' = 2d²

(9) We note that u', v' have the following properties:

(a) gcd(u',v')=1

Assume there is a prime f that divides both c + 5d², 2d².

There are three cases that we need to consider:
Case I: f = 2
Case II: f = 5
Case III: f divides both c,d

Case I isn't true because u' = c + 5d² is odd since c,d have different parities (#8) and in both cases, u' is odd:

(odd) + 5(even)² = odd + even = odd
(even) + 5(odd)² = even + odd = odd

Case II isn't true 5 doesn't divide c (#8)

Finally Case III isn't true since gcd(c,d)=1 (#8)

(b) 5 doesn't divide u', 5 divides v'

We know that 5 divides d (#8b) so 5 divides v'=2d². 5 doesn't divide u' since gcd(u',v')=1 (#8)

(c) u',v' have different parities

v' is even by definition. We showed already that u' is odd (#10a)

(d) u' - 5v'² is a fifth power since:

c⁴ + 10c²d² + 5d⁴ can be put into the form (c² + 5d²)² - 5(2d²)² since:

(c² + 5d²)² = c⁴ + 10c²d² + 25d⁴ [From the Binomial Theorem]

5(2d²)² = -20d⁴

Now, (2*5²r) is a fifth power (#7e) so (2*5²r)² is a fifth power [since (x⁵)² = (x²)⁵]

(2*5²r)² = 2*5³*10r² = (2*5³)*v = (2*5³)[5d(c⁴ + 10c²d² + 5d⁴)] =
(2*5⁴d)(c⁴ + 10c²d² + 5d⁴)

So, we next show that gcd( 2*5⁴d ,c⁴ + 10c²d² + 5d⁴ ) = 1

Assume that there is a prime f that divides both. We need handle three cases:

Case I: f = 2
Case II: f=5
Case III: f divides both c,d

Case I is impossible since c⁴ + 10c²d² + 5d⁴ is odd since c,d have different parities (#8) and:
(odd)⁴ + 10(odd)²(even)² + 5(even)⁴ = odd + even + even = odd
(even)⁴ + 10(even)²(odd)² + 5(odd)⁴ = even + even + odd = odd

Case II is impossible since 5 doesn't divide c (#8)

Case III is impossible since gcd(c,d)=1 (#8)

OK, combining these results with Relatively Prime Divisors of n-powers, we can conclude that:
2*5⁴d and c⁴ + 10c²d² + 5d⁴ are 5th powers.

(10) With the properties in step #9, we can use a lemma which I will prove later to show:

c + 5d² = c'(c'⁴ + 50c'²d'² + 125d'⁴)

2d² = 5d'(c'⁴ + 10c'²d'² + 5d'⁴)

gcd(c',d')=1

c',d' have different parities

5 doesn't divide c'

5 divides d'

c' , d' ≠ 0

(11) (2*5⁸)(2d²) = 2²*5⁸d² = (2*5⁴d)²

(12) We know that 2*5⁴d is a fifth power from step (#9d) so (2*5⁴d)² is also a fifth power [Because (x⁵)² = (x²)⁵]

(13) So 2*5⁹d'(c'⁴ + 10c'²d'² + 5d'⁴) is a fifth power by the argument below:

First, we note that (2*5⁸)(2d²) is a fifth power since:
(2*5⁸)(2d²) = (2*5⁴d)² (from step #11) and (2*5⁴d)² is a fifth power (from step #12)

But this shows that 2*5⁹d'(c'⁴ + 10c'²d'² + 5d'⁴) is a fifth power since:
2*5⁹d'(c'⁴ + 10c'²d'² + 5d'⁴) = (2*5⁸) * 5d'(c'⁴ + 10c'²d'² + 5d'⁴) = (2*5⁸)(2d²) [from step #10.]

(14) gcd(2*5⁹d' , c'⁴ + 10c'²d'² + 5d'⁴)=1 since:

(a) Assume there is a prime f that divides both 2*5⁹d' and c'⁴ + 10c'²d'² + 5d'⁴.

(b) There are three cases that we need to consider by Euclid's Generalized Lemma:

Case I: f = 2
Case II: f = 5
Case III: f divides d' and c'⁴ + 10c'²d'² + 5d'⁴

(c) We can eliminate Case I since is c'⁴ + 10c'²d'² + 5d'⁴ odd.

c',d' have opposite parity (#10) which means that the value is odd

(even)⁴ + 10(even)²(odd)² + 5(odd)⁴ = even + even + odd = odd

(odd)⁴ + 10(odd)²(even)² + 5(even)⁴ = odd + even + even = odd

(d) We can eliminate Case II since 5 doesn't divide c' which 5 cannot divide c'⁴ + 10c'²d'² + 5d'4. [Detail if needed is here]

(e) We can eliminate Case III since gcd(c',d') = 1. [From step (#10)]

(15) So 2*5⁹d' and c'⁴ + 10c'²d'² + 5d'⁴ are also fifth powers. [By (#14) and Relatively Prime Divisors of n-powers]

(16) Step (#15) puts us in the exact same position as Step (#9). This means that using the same argument, we can apply the lemma (see Lemma 1, here) as many times as we would like.

(17) Moreover, d' is greater than 0 and d' is less than d since:

25d'⁵ ≤ 5d'(c'⁴ + 10c'²d'² + 5d'⁴) = 2d² [From steps (#10) since c',d' are nonzero and therefore c'² and d'² ≥ 1]

We note that 5d'(c'⁴ + 10c'²d'² + 5d'⁴) = 25d'⁵ + 5d'(c'⁴ + 10c'²d'²)

Also:

25d'⁵ ≤ 2d² → d'⁵ ≤ (2d²)/25 → d' ≤ ⁵√(2d*2d)/25

So:

d' is less than d [Since ⁵√(2d*2d)/25 is less than d as shown below]

⁵√(2d*2d)/25 is less than d since

(i) Putting both sides to the power of 5 gives us:
(2d²)/25 is less than d⁵

(ii) Multiplying both sides by 25 gives us:
2d² is less than 25d⁵

(iii) Since d ≥ 1 (#7), we know that d² is less than d⁵.

(18) If this procedure continued, we eventually get an integer d'' which is less than 1 which is absurd [We only need to repeat this procedure d more times]

QED

Fermat's Last Theorem: Proof for n=5

For those interested in the history behind this proof, you may want to start here.

The proof presented is based on two books: Harold M. Edward's Fermat's Last Theorem: A Genetic Introduction and Paulo Ribenboim's Fermat's Last Theorem for Amateurs.

Theorem: Proof for FLT: n=5

x⁵ + y⁵ = z⁵ → xyz = 0 if x,y,z are integers.

(1) Assume there is a solution where xyz ≠ 0

(2) From previous results, we know that we can assume that gcd(x,y,z)= 1 (see here).

(3) We can also assume that x,y are odd and z is even since:

(a) We know that at least two of the values are odd since gcd(x,y,z)=1 tells that only 1 at most can be even.

(b) If two are odd, then the third is even since odd + odd = even and odd - odd = even.

(c) If z is even we are good so let's assume that x is even.

We know that there exists z', x' such that z' = -z and x' = -x so x' is even:

(-1)⁵(x')⁵ + y⁵ = (-1)⁵(z')⁵

First, we add (z')⁵ to both sides to give us:

(-1)⁵(x')⁵ + y⁵ + (z')⁵ = 0.

Then, we add (x')⁵ to both sides to give us:

y⁵ + (z')⁵ = (x')⁵

Even in this case, we have derived a form z⁵ = x⁵ + y⁵ where z is even.

(4) We can assume that 5 divides xyz from Sophie's proof.

(5) Now, it can be shown that if 5 divides z, then there is no integer solution (see here for proof) and likewise, it can be show if 5 doesn't divide z, then there is no integer solution (see here for proof).

(6) So we have a contradiction and can reject our initial assumption.

QED

Johann Dirichlet

Johann Peter Gustav Lejeune Dirichlet was born on February 13, 1805 in Duren which at the time was part of Napoleon's empire. His family had originally come from Richelet, Belgium which is why his family name was Dirichlet which means 'from Richelet.'

From an early age, he showed a fascination with mathematics. By the age of 12 when he started at the Gymnasium in Bonn, he would routinely spend his pocket money on math books. At school, he was a model student and after two years, transfered to the Jesuit College in Cologne. By the time he graduated, he decided to seek an education in Paris. There, he was able to attend lectures by some of most famous mathematicians of the time including Fourier, Laplace, Legendre, and Poisson.

In 1823, he began to work for the family of General Maximilien Sébastien Foy. Dirichlet taught German to Foy's wife and children. Dirichlet chose at this time to work on his first paper which concerned Fermat's Last Theorem for n=5. At this time, case for n=3 and n=4 had already been solved. In 1825, Dirichlet succeeded in proving it true for the case where one of the numbers x,y,z is divisible by 10. The paper attracted a lot of attention and one of his reviewers was Adrien Legendre. Shortly after the presentation Legendre was able to complete the proof for n=5. Dirichlet also came up with a complete proof but did so only after Legendre had published his complete solution for n=5. In addition, he wrote a very important paper on biquadratic reciprocity which extended a result by Gauss.

Around this time, General Foy died and Dirichlet returned to Germany. He sought employment but was denied because of the requirement that he needed to have completed a doctoral thesis. This problem was solved when he was given an honorary doctorate from the University of Cologne. He then acquired a post at the University of Breslau. Despite his fame from his result with Fermat's Last Theorem, his appointment at the University of Breslau created a great controversy among the German math professors.

Dirichlet found the standards at the university were disappointingly low and in 1828, he transferred to the University of Berlin. He remained there until 1855. Later, he would help to greatly raise the mathematical standards in Germany.

In 1831, he was appointed to the Berlin Academy. By this time, he was paid enough to consider marriage. He married Rebecca Mendelsohn who was a sister to the composer Felix Mendelsohn. At this time, he also corresponded with the mathematician Jacobi. Together, their correspondences exerted a tremendous influence on number theory.

In 1837, he proved a conjecture by Gauss on the arithmetic progression of primes that clarified a result done earlier by Legendre. His work would later form the foundation of analytic number theory and algebraic number theory. That same year he proposed what is today the modern definition of a function. Other work included potential theory, integration of hydrodynamic equations, convergence of trigonometric series, and fourier series.

In 1855, after Gauss's death, Dirichlet took over Gauss's post in Gottingen. He was very happy in Gottingen but unfortunately, his stay there did not last long. In 1858 while lecturing at a conference in Montreux, he suffered a near fatal heart attack. When he returned to Gottingen, he learned that his wife had just died of a stroke. He died shortly afterwards in May of 1859.

References

• Biography of Dirichlet, MacTutor
  

Adrien-Marie Legendre

Adrien-Marie Legendre did not like to talk about his personal life. His colleague Simeon Poisson wrote:

Our colleague has often expressed the desire that, in speaking of him, it would only be the matter of his works, which are, in fact, his entire life. (From MacTutor Biography)

He was born September 15, 1752 in France. He may have been born in Toulouse but from a very early time, his family lived in Paris. His family was wealthy and he attended the College Mazarin in Paris. His area of focus was mathematics and physics.

In 1775, he became a lecturer at the Ecole Militaire based on the recommendation of the well known mathematician Jean D'Alembert. One of his fellow lecturers at the Ecole Militaire was Pierre-Simon Laplace who would later become very well known himself.

Legendre's reputation was made when he was able to win the Berlin Academy Prize in 1782. The Berlin Academy had proposed a very difficult problem that involved calculating the projectory path of a cannon ball undergoing air resistance. He later wrote an influential paper on the force of attraction between two confocal ellipsoids. In January of 1783, he was appointed as an associate to the French Academy of Sciences.

Legendre proceeded to do influential investigations of celestrial mechanics, number theory, and elliptic functions. In number theory, his work includes an important result on the quadratic reciprocity of residues and arithmetic progressions of prime numbers. Both of these results were later superceded by Carl Friedrich Gauss's work on quadratic reciprocity of residues and Johann Dirichlet's work on arithmetic progressions of primes. In 1787, he was elected to the Royal Society of London.

After the French Revolution of 1793, Legendre lost most of his fortune. In 1794, he published his Elements of Geometry which became the leading elementary text on geometry at the time. In this work, he attempted to make the proofs behind Euclid's Elements clearer and better organized.

In 1801, Gauss criticized Legendre's results on quadratic reciprocity and claimed that he himself had invented the correct method. It is clear that Legendre was not happy with Gauss's words but in 1808, when Legendre came out with the next version of his textbook on number theory, he included Gauss's proof instead of his own.

In 1824, Legendre refused to support the government's candidate for the National Institute. As a result of his refusal, he lost his pension and lived his remaining years close to poverty.

In 1830, he offered his proof for Fermat's Last Theorem n = 5 which was based on the work done by Dirichlet and also the proof by Sophie Germain.

Legendre was fascinated by Euclid's parallel postulate and for many years attempted to provide a proof. He refused to believe in the existence of non-Euclidean geometries which were first proposed by Nikolai Ivanovich Lobechevsky in 1829.

Legendre died on January 10, 1833. He had made significant achievements in geometry, differential equations, calculus, function theory, number theory, and statistics.

References

• Biography of Legendre, MacTutor
• Legendre, Wikipedia
  

Continued Fractions

The proof for Fermat's Last Theorem n = 5 depends on Continued Fractions. A Continued Fraction is an expression of the following form:


where a₀, a₁, etc. are all integers. To simplify this characterization, the Continued Fraction is represented using the following notation:
[ a₀, a₁, a₂, ... ]

To understand the power of continued fractions, let's look at how they can be used to represent the square root of 2. Being an irrational number, the digits that make up the real number do not repeat (if they repeated, then it would not be an irrational number, see here). The digits we get are: 1.4142135...

Using continued fractions, we can represent this same value as [1,2,2,2...] where 2 repeats for ever (see below).

Continued Fractions as an idea have their origin withEuclid's Algorithm for finding the greatest common denominator of two integers. Popular study of Continued Fractions began with the work of John Wallis who was the first to use the term "continued fractions."

Later, Leonhard Euler established the foundations of continued fractions. He demonstrated, for example, that every rational number can be expressed as a terminating, simple continued fraction, established a formula for the constant e in continued fraction form, and used this to prove that e is irrational (more on this in a future blog)

Other important work was done by Joseph Louis Lagrange. He used continued fractions to show the value of irrational roots and proved that the real root of a quadratic irrational is a periodic continued fraction (more on this result in a future blog).

The story of continued fractions goes greatly beyond this short outline. For those interested in understanding the larger story, please check out the references at the bottom of this blog.

First, it should be clear that all real numbers can be represented as continued fractions.

Lemma 1: We can generated a continued fractions of the form [ a₀, a₁, a₂, ... ] for any real number.

(1) Let α be any real number.
(2) Let's define a function floor() such that the floor() of any real number is the highest integer that is lower than the real number. For example floor(π) = 3.
(3) Now, here are the rules for constructing the continued fraction:
(i) Let α₀ = α
(ii)Let a_n = floor(α_n)
(iii) Let α_n+1 = 1/(α_n - a_n)
(4) For any integer, the continued fraction is [a₀] since floor(any integer) = the integer.
(5) If it is not an integer, then we use (iii) to get α₁ and use (ii) to determine a₁.
(6) In this way, we can generate a continued fraction for any real value.

QED

As an example, let's use the algorithm above to generate the continued fraction for √2:

Corrolary: √2 = [ 1,2,2,2...]

(1) a₀ = floor(√2) = 1.

(2) α₁ = 1/(√2 - 1) =√2 + 1 [By multiplying both sides by √2 + 1 ]

(3) a₁ = floor(√2 + 1) = floor(√2) + 1 = 2

(4) α₂ = 1/(√2 + 1 - 2) = 1/(√2 - 1) = √2 + 1.

(5) This means that we are at the same value as step (2) which means that the value 2 goes on ad infinitum.

QED

References

• Continued Fractions, Wikipedia
• Continued Fractions, Mathworld
• An Introduction to Continued Fractions
  
• Continued Fractions, Cut-the-knot
  

Joseph-Louis Lagrange

Joseph-Louis Lagrange was born in Turin, Italy on January 25, 1736. His original name was Giuseppe Luigi Lagrangia. He would later change his name as he made Prussia and France his home.

His father was a well-to-do mechant who worked for the King of Sardinia. Unfortunately, due to speculations, his father lost much of his wealth. Lagrange went to the college of Turin. He became interested in mathematics when he was 17 and he discovered a paper by Edmund Halley. Within one year, he had impressed the college with his skills in mathematics and became a lecturer at the artillery school.

When Lagrange was 19, he sent a letter to the famous mathematician Leonhard Euler describing a solution to the isoperimetrical problem. Euler was very impressed with Lagrange's method and conceded that it was superior to his own. Euler had been planning to publish his solution to the problem but after viewing Lagrange's solution, he withdrew his paper and let Lagrange publish the first solution to the problem. This paper helped to establish Lagrange as one of the top mathematicians of his time. The solution would serve as the foundation for what became known as the calculus of variations.

In 1758, Lagrange organized the Turin Academy which was a mathematical society that focused on mathematics. This group would go on to publish 5 volumes of mathematics. These volumes presented very high quality mathematics including topics such as a theory of the propagation of sound, a general differential equation for motion, a complete solution to an equation for a string vibrating traversely, recurring series, probabilities, more details on the calculus of variations, the principle of least action, integral calculus, number theory, and general differential equations for the motion of three bodies. By 1761, Lagrange had established himself as one of the greatest mathematician living. In 1764, he began his study of the libations of the moon and published his mathematical explanation for why the moon only displays the same face to the earth.

In 1766, Euler left Berlin. Frederick the Great invited Lagrange to come fill his post. Frederick wrote that the "greatest king in Europe" would like to have the "greatest mathematician of Europe" as resident in his royal court. Lagrange accepted his invitation and would stay in Prussia for the next 20 years.

While in Prussia, he wrote his famous Mecanique Analytique. His productivity at this point was amazing. He was producing a very high quality mathematical paper at the rate of one per month. He would spend his time thinking through each of his ideas and only when he had thought his ideas through did he write his papers. It is said that he was able to write out his papers complete without a single correction required. Topics included astronomical observations, pressure exerted by fluids in motion, integration by infinite series, a paper on the Jovian system, an essay on the problem of three bodies, secular equations of the moon, and cometary pertubations. In the course of these papers, he won many of the prizes (1772, 1774, and 1780) that were offered by the French Academy. Between 1772 and 1788, he worked to simplify Newton's equations. He reformulated Newtonian mechanics creating what is today known as Lagrangian mechanics.

In 1787, Frederick died and Lagrange accepted the offer of Louis XVI to move to Paris. He turned down invitations from Spain and Naples. He set up in residence in one of the special apartments of the Louvre. In 1792, he married for the second time.

The Reign of Terror began in 1793. In September 1793, an order was placed requiring all foreigners to leave France. He was able to get an exemption to this order based on the help of Antoine Lavoisier. Later, in 1798, his friend Lavoisier, after a trial that lasted only a day, was put to death by guillotine.

Lagrange wrote of his friend:

It took only a moment to cause this head to fall and a hundred years will not suffice to produce its like.

In 1797, he became a professor of the Polytechnique Ecole in Paris. His lectures at the Polytechnique became very important and influential mathematical papers. It was here that he did his work on Continued Fractions and his mentorship of Sophie Germain.

Lagrange was still working on a revision of his Mecanique Analytique when he died in 1813. His achievements are astounding. He is one of the most prolific and important mathematicians of all time.

References

• Joseph-Louis Langrange, Wikipedia
• Biography of Lagrange, MacTutor
  

Binomial Theorem

The Binomial Theorem was first presented by Sir Isaac Newton. He came up with this principle based on the work done by Blaise Pascal (Pascal's Triangle) and Pierre de Fermat. Newton's result is actually deeper than the one presented in today's blog. He was able to generalize the Binomial Theorem to include exponents that could be any real number. When the Binomial Theorem is presented in this context, it is often refered to as the Binomial Series.

The proof presented here relies on the Principle of Mathematical Induction. If you are not familiar with Mathematical Induction, then you may wish to start here.

The proof is based on factorials. Importantly, it relies on the following definition:



With this definition in mind, let's take a look at the proof for the Binomial Theorem:

Theorem: Binomial Theorem


(1) The assumption here is that n ≥ 2. For n=1, we know that (a+b)¹ = a¹ + b¹ = a + b.

(2) Let S be the set of all numbers n ≥ 2 that supports the binomial theorem. If there are no such numbers, then S would be empty.

(3) We know that 2 is an element of S since:

(a) (a + b)² = a² + 2ab + b² (See here for details if needed)

(b)


= a² + 2ab + b²

(4) So, let us suppose that there is a value n such that 2 thru n, the binomial theorem holds. If the binomial theorem, for example, didn't hold for 3, then n would equal 2.

(5) Now, we note that:
(a + b)ⁿ⁺¹ = (a + b)ⁿ(a + b) = a(a + b)ⁿ + b(a + b)ⁿ

(6) Now, by (4), we have:






and







(7) The trick comes down to realizing that:



(a) We notice that m=0 thru n-1 and m=1 thru n contains the same number of elements.

(b) At each point, m as a value of the factorial expression is the same. In the case of m = 0, the first element is 0, the second element is 1, and so on until we get to n-1. In the case of m=1, the first element is 0, the second element is 1, and so on until we get to n.

(c) At each point, the exponent for a is the same. In the case of m=0, the first exponent is n-m = n, the second coefficient has a power of n-1, followed by n-2, and so on until we get to n-(n-1) = 1. In the case of m=1, the first exponent is n-m+1=n, the second coefficient has a power of n-1 and so on until we get to the last one which is n-n+1 which is equal to 1.

(d) Finally, at each point, the exponent for b is the same. In the case of m=0, the first power of b is 1, followed by 2, and so on until we get to n-1+1 which = n. In the case of m=1, the first power of b is 1, followed by 2, and so until we get to the end which b to the power of n.

(8) Applying our results from (6) and (7) and applying Pascal's Rule, we note that:



Which gives us that:



(9) And putting this all together, gives us:



QED

Pascal's Triangle and Pascal's Rule

Before we can proceed to the Binomial Theorem, we need to review a lemma that was introduced in the west by Blaise Pascal and which is today known as Pascal's Rule. The rule itself stems from an analysis of Pascal's Triangle.

Pascal's rule requires a basic understanding of the mathematics of permutations which concerns the problem of counting the number of different selections that can be made from a given set. For those who would like a review of the basic ideas of permutations and factorials, please start here. Some examples are below.

If we have only 1 element, then there is only 1 way of selecting 1 element. But if we have 2 elements, we have 2 different ways to select 1 element. If we have 15 elements, then there are 15 different ways to select 1 element and, it turns out, (15*14)/2 ways to select 2 elements. In other words, if we have n total elements and we want to select m of them, there are exactly n!/[m!(n-m)!] ways to select them where order doesn't matter. (See here for further explanation)

The formula for counting the number of ways to select m elements from a set of n total elements can be characterized by this shorthand notation:


In the case of selecting 2 items out of 15, we get the following:


Which gives us: 15!/(2!)(13)! = (15*14)/2.

With these ideas in mind, we can proceed to look at Pascal's Triangle. Pascal's Triangle is a way to characterize exponents such as (a + b)ⁿ

For example, the Triangle starts out as follows:

(n=0) 1
(n=1) 1 1
(n=2) 1 2 1
(n=3) 1 3 3 1
(n=4) 1 4 6 4 1
...

In each case, the number in the next row is equal to the sum of the two numbers above it (and if only one number is above it, then it is equal to this one number). We can keep on going as long as we like.

Let's see how this maps into the equation (a+b)ⁿ

(a + b)⁰ = (1)1
(a + b)¹ = (1)a +(1) b
(a + b)² = (1)a² + (2)ab + (1)b²
(a + b)³ = (1)a³ + (3)a²b + (3)ab² + (1)b³
(a + b)⁴ = (1)a⁴ + (4)a³b + (6)a²b² + (4)ab³ + (1)b⁴

It turns out that each element of Pascal's Triangle can be built from an equation using the above equation. If we remember that 0! = 1, then we get the following

For n = 0, the single element is equal to:


For n = 1, each element can be described by the notation below:


For n = 2, each element can be described by:




For n = 3, each element can be described by:


And so on.

This is useful because it allows to pick any exponent n and generate the list of coefficients that make up its values.

For example, we know that the coefficients for n=7 will be:


So far so good. But wait a minute. When we were creating the triangle from step 1, we were adding each coefficient from the previous values. Is there a relationship here that can be captured in terms of the equation?

This is Pascal's Rule which is presented below.

Lemma: Pascal's Rule:




(1)







(2)



(3) Now, the trick is to be able to add both of these values as fractions. This can be done based on the following equalities:

m! = (m)(m-1)!
(n-m)! = (n-m)(n-m-1)!

(4) Applying (3) to (1) and (2) gives us:








QED