(45)x - (3,795)x3 + (95,634)x5 - (1,138,500)x7 + (7,811,375)x9 - (34,512,075)x11 + (105,306,075)x13 - (232,676,280)x15 + (384,942,375)x17 - (488,494,125)x19 + (483,841,800)x21 - (378,658,800)x23 + (236,030,652)x25 - (117,679,100)x27 + (46,955,700)x29 - (14,945,040)x31 + (3,764,565)x33 - (740,259)x35 + (111,150)x37 - (12,300)x39 + (945)x41 - (45)x43 + x45 =
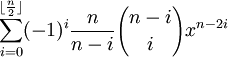
where n = 45.
In today's blog, I will show how a recurrence relation can be introduced to simplify the problem further.
The key insight comes to generalizing the above summation formula. For example, let's define:
Fn(x) =
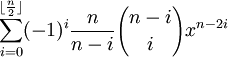
It turns out that it is possible to show that for any n ≥ 1:
2cos(nα) = Fn(2cosα)
For any odd n ≥ 1:
2 sin(nα) = (-1)(n-1)/2*Fn(2sinα)
François Viète knew both of these identities and he would use them to find his solutions to Van Roomen's problem. In today's blog, I will show the proof for the recurrent relation and in my next blog, I will show how this recurrence relation leads to the trigonometric identities above.
Theorem 1: Recurrence Formula
If:
Fn(x) =
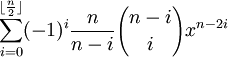
Then:
Fn(x) = x*Fn-1(x) + Fn-2(x)
Proof:
(1) F1(x) = (-1)0*(1/1)*[(1!)/(0!1!)]x1-0 = x
(2) F2(x) = (-1)0*(2/2)*[(2!)/(0!2!)]x2-0 + (-1)1*(2/1)*[(1!)/(1!0!)]x2-2 = x2 - 2
(3) F3(x) = (-1)0*(3/3)*[(3!)/(0!3!)]x3-0 + (-1)1*(3/2)*[(2!)/(1!1!)]x3-2 = x3 - 3x
(4) We can see that x*F2(x) - F1(x) = x*(x2 - 2) - x = x3 - 3x.
(5) So, we can assume that the recurrence formula is true up to some integer n-1 where n ≥ 4, that is:
Fn-1(x) = x*Fn-2(x) - Fn-3(x)
(6) Now, x*Fn-1(x) =

=

(7) Likewise, Fn-2(x) =

=

=

(8) So, we see that: x*Fn-1(x) - Fn-2(x) =


where if n is odd,
C = 0
and if n is even,
C =
-(-1)(n/2 - 1)[(n-2)/(n-1-n/2)][(n-1-n/2)!/(n/2-1)!(n-1-n/2-(n/2-1))!]xn-2(n/2) =
= (-1)(n/2)[(n-2)/(n/2-1)][(n/2-1)!/(n/2 -1)!(0!)]x0 =
= (-1)(n/2)[(n-2)]/[(n/2-1)](1)(1) = (-1)(n/2)(n-2)*(2)/(n-2) =
= (-1)(n/2)*2
(9) So, x*Fn-1(x) - Fn-2(x) - C - xn =

(10) Focusing solely on the middle part, we see that:







(11) If n is odd:
Fn(x) =

(12) If n is even:
Fn(x) =

(13) So, either way we have:
Fn(x) = x*Fn-1(x) - Fn-2(x).
QED

No comments:
Post a Comment