(45)x - (3,795)x3 + (95,634)x5 - (1,138,500)x7 + (7,811,375)x9 - (34,512,075)x11 + (105,306,075)x13 - (232,676,280)x15 + (384,942,375)x17 - (488,494,125)x19 + (483,841,800)x21 - (378,658,800)x23 + (236,030,652)x25 - (117,679,100)x27 + (46,955,700)x29 - (14,945,040)x31 + (3,764,565)x33 - (740,259)x35 + (111,150)x37 - (12,300)x39 + (945)x41 - (45)x43 + x45 = A
where:
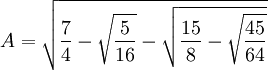
Each of the coefficients is large and none of them are prime. Nineteen of them, for example, are divisible by 5. 95,634 is divisible by 7. 236,030,652 is divisible by 12. 740,259 is divisible by 3.
In addition, if we examine the coefficients in series from x1 thru x45, we can see that they are smallest at the edges and progressively larger toward the middle. This is a pattern also exhibited by binomials such as (x + y)n.
François Viète was able to reformulate's Adriaan van Roomen's equation into a summation equation. Using modern notation, he reduced the problem to:
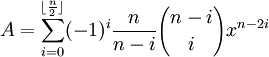
where:
n = 45
 = the largest integer ≤ n/2
= the largest integer ≤ n/2
[See here for review of factorial (!) if needed]
The floor(n/2) function is used because we only want to generate 22 different terms. Van Roomen's equation consists solely of odd powers.
If you want to see that it works, you can work it out for each term. Here are some examples of how the summation formula works:
At i=0:
(-1)0*(45/45)*[(45)!/(0!45!)]x45 = x45
At i=1:
(-1)1*(45/44)[(44)!/(1!43!)]x43 = -45x43
Let's skip to i=11:
(-1)11*(45/34)*[(34)!/(11!23!)]x23 = -(45*33!)/(11!23!)x23 = -(378,658,800)x23
and so on up to i=22:
(-1)22*(45/23)*[(23)!/(22!1!)]x1 = 45x
In my next blog, I will show how a recurrence relation can further simplify the problem.
References
- Jean-Pierre Tignol, Galois' Theory of Algebraic Equations
, World Scientific, 2001

No comments:
Post a Comment