In today's blog, I will show how de Moivre derived his formula based on Francois Viete's solution of Van Roomen's Problem.
Theorem 1: De Moivre's Formula

Proof:
(1) Let x = 2 cos(α)
(2) Let l = cos(nα)
(3) We can define z such that:

(4) So that:
zn = l + √l2 - 1
So that:
zn - l = √l2 - 1
and:
(zn - l)2 = l2 - 1
(5) Working through the equation in step #4, we get:
(zn - l)2 = z2n - 2lzn + l2 = l2 - 1
Subtracting l2 - 1 from both sides gives us:
z2n - 2lzn + 1 = 0
(6) Now, from a Viete's famous solution to Van Roomen's problem (see Corollary 1.1, here), we have:
2 cos(nα) = fn(2 cos α)
where:
fn(x) =

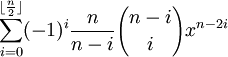
(7) Putting step #6 in step #5 gives us:
z2n - 2*(1/2)fn(x)zn + 1 = z2n - fn(x)zn + 1 =0
(8) For n=1, we have:
z2(1) - f1(x)z1 + 1 = 0
(9) Now using the definition for fn(x) in step #6 above, we can see that:
f1(x) = (-1)0(1/[1-0])([1-0]!/0![1 - 2*0]!)x1 - 2*0 =
= 1*(1/1)(1!/[0!1!])x1 =
= x
(10) This then gives us:
z2 - xz + 1 = 0
(11) Now using the quadratic equation to solve for z (see Theorem, here) gives us:
z = (x ± √x2 - 4)/2 =
= x/2 ± √(x/2)2 - 1
(12) Since x = 2cos(α), this gives us:
z = [2 cos(α)]/2 ± √[2 cos(α)/2]2 - 1 =
= cos(α) ± √cos2(α) - 1
(13) Since cos2(x) + sin2(x) = 1 [See Corollary 2, here], we have:
z = cos(α) ± √cos2(α) - 1 =
= cos(α) ± √(-1)[1 - cos2(α)] =
= cos(α) ± √(-1)sin2(α) =
= cos(α) ± [√(-1)]sin(α)
(14) Since l = cos(nα), from step #2 above, we have:





(15) Putting step #13 and step #14 together gives us:

QED
You might notice that De Moivre's result is ambiguous. Since there are n roots, it is impossible that its result could only be two possible values. This problem was not evident until after there was deeper understanding of the fundamental theorem of algebra. Interestingly, this fundamental theorem was not well understood until after De Moivre's discovery of the roots of unity which I will talk about in my next blog.
The corrected version of de Moivre's formula is:
cos(nα) + isin(nα) = [cos(α) + isin(α)]n
References
- Jean-Pierre Tignol, Galois' Theory of Algebraic Equations
, World Scientific, 2001

1 comment:
That is really cool! It took me a while to understand a little bit, but you did a great job explaining it.
Post a Comment