Today's blog continues the proof for Fermat's Last Theorem: n= 5. If you are interested in the history behind the proof, start here. If you are interested in the mathematical details behind the proof, start here.
Today's blog rests on the proof offered by Paulo Ribenboim in Fermat's Last Theorem for Amateurs.
Lemma 1: Given a,b,x such that:
(a) a,b,x are integers
(b) a,b have different parities
(c) gcd(a,b)=1
(d) a,b are nonzero
(e) 5 doesn't divide a
(f) 5 divides b
(g) a2 - 5b2 = x5
(h) there exist integers h,k such that: a + b√5 = ([h + k√5]/2)5
(i) h,k have the same parity
Then h,k are even.
(1) 25b = 5k(h4 + 10h2k2 + 5k4) since:
(a) (h + k√5)5 = h5 + 5h4k√5 + 50h3k2 + 50h2k3√5 + 125hk4 + 25k5√5.
(b) From (a) and from (h) above: 25b = 5h4k + 50h2k3 + 25k5 [25 is necessary since a + b√5 = [h + k√5] divided by 25
(c) From (b), 25b = 5k(h4 + 10h2k2 + 5k4)
(2) Assume that h,k are odd
(3) From (c), we know that 32 must divide (h4 + 10h2k2 + 5k4) since 2 doesn't divide 5 and since 2 doesn't divide k (since we are assuming in #2 that k is odd)
(4) h4 or k4 ≡ 1 or 17 (mod 32) since (the argument for h below applies equally to k):
(a) h is odd so h ≡ 1 (mod 2) which means that h modulo 32 could be any odd number including ±1, ± 3, ± 5, and so on until ± 15.
(b) h2 modulo 32 can only be congruent to 1, 9, 17, or 25 (see here for a review of modular arithmetic)
(±1)2 ≡ 1 (mod 32)
(±3)2 ≡ 9 (mod 32)
(±5)2 ≡ 25 (mod 32)
(±7)2 ≡ 49 ≡ 17 (mod 32)
(±9)2 ≡ 81 ≡ 17 (mod 32)
(±11)2 ≡ 121 ≡ 25 (mod 32)
(±13)2 ≡ 169 ≡ 9 (mod 32)
(±15)2 ≡ 225 ≡ 1 (mod 32)
(c) h4 modulo 32 can only be congruent 1 or 17.
(1)2 ≡ 1 (mod 32)
(9)2 ≡ 17 (mod 32)
(17)2 ≡ 289 ≡ 1 (mod 32)
(25)2 ≡ 625 ≡ 17 (mod 32)
(5) For h4 ≡ 1 (mod 32), we know that h2 ≡ 1 or 17 (mod 32)
(6) For h4 ≡ 17 (mod 32), we know that h2 ≡ 9 or 25.
(7) But from our assumption in #2, we find that 32 cannot divide (h4 + 10h2k2 + 5k4) since modulo 32 it is congruent to 16 (see below)
Case h4 ≡ 1, k4 ≡ 1:
(1) + 10(1)(1) + 5(1) ≡ 1 + 10 + 5 ≡ 16 (mod 32)
(1) + 10(17)(1) + 5(1) ≡ 1 + 170 + 5 ≡ 1 + 10 + 5 ≡ 16 (mod 32)
(1) + 10(1)(17) + 5(1) ≡ 1 + 170 + 5 ≡ 1 + 10 + 5 ≡ 16 (mod 32)
(1) + 10(17)(17) + 5(1) ≡ 1 + 2890 + 5 ≡ 1 + 10 + 5 ≡ 16 (mod 32)
Case h4 ≡ 17, k4 ≡ 1:
(17) + 10(9)(1) + 5(1) ≡ 17 + 90 + 5 ≡ 17 + 26 + 5 ≡ 16 (mod 32)
(17) + 10(25)(1) + 5(1) ≡ 17 + 250 + 5 &eqiuv; 17 + 26 + 5 ≡ 16 (mod 32)
(17) + 10(9)(17) + 5(1) ≡ 17 + 1530 + 5 ≡ 17 + 26 + 5 ≡ 16 (mod 32)
(17) + 10(25)(17) + 5(1) ≡ 17 + 4250 + 5 ≡ 17 + 26 + 5 ≡ 16 (mod 32)
Case h4 ≡ 1, k4 ≡ 17:
(1) + 10(1)(9) + 5(17) ≡ 1 + 90 + 85 ≡ 1 + 26 + 21 & equiv; 16 (mod 32)
(1) + 10(17)(9) + 5(17) ≡ 1 + 1530 + 85 ≡ 1 + 26 + 21 & equiv; 16 (mod 32)
(1) + 10(1)(25) + 5(17) ≡ 1 + 250 + 85 &eqiuv; 1 + 26 + 21 ≡ 16 (mod 32)
(1) + 10(17)(25) + 5(17) ≡ 1 + 4250 + 85 ≡ 1 + 26 + 21 & equiv; 16 (mod 32)
Case h4 ≡ 17, k4 equiv; 17
(17) + 10(9)(9) + 5(17) ≡ 17 + 810 + 85 ≡ 17 + 10 + 21 ≡ 16 (mod 32)
(17) + 10(25)(9) + 5(17) ≡ 17 + 2250 + 85 ≡ 17 + 10 + 21 ≡ 16 (mod 32)
(17) + 10(9)(25) + 5(17) ≡ 17 + 2250 + 85 ≡ 17 + 10 + 21 ≡ 16 (mod 32)
(17) + 10(25)(25) + 5(17) ≡ 17 + 6250 + 85 ≡ 17 + 10 + 21 ≡ 16 (mod 32)
(8) So we have a contradiction and we reject our assumption.
QED
Lemma 2: Given a,b such that:
(a) gcd(a,b)=1
(b) a,b have different parities (one is odd, one is even)
(c) a,b are nonzero
(d) 5 doesn't divide a
(e) 5 divides b
(f) a + b√5 = [(m + n√5)/2]5([t+u√5]/2) where u = 0.
Then:
(a) a = c(c4 + 50c2d2 + 125d4)
(b) b = 5d(c4 + 10c2d2 + 5d4)
(c) gcd(c,d)=1
(d) c,d have different parities
(e) 5 doesn't divide c
(f) c,d are nonzero
Proof:
(1) We know that there exists m',n' such that:
(m' + n'√5)/2 = [(m+n√5)/2]5= (m5 + 5m4n√5 + 50m3n2 + 50m2n3√5 + 125mn4 + 25n5√5)/25
(2) So, m' = (m5 + 50m3n2 + 125mn4)/24
(3) This means that 16m' ≡ m5 (mod 5)
(4) So, n' = (5m4n + 50m2n3 + 25n5)/24
(5) This means that 16n' ≡ 0 (mod 5) and 5 divides n'.
(6) a + b√5 = [(m' + n'√5)/2][(t + u√5)/2] = (m't + m'u√5 + n't√5 + 5n'u)/4
(7) So:
4a = m't + 5n'u
4b = m'u + n't
(8) From this we can conclude that 5 doesn't divide m' (otherwise from #7, 5 would divide a which it does not)
(9) We can also conclude that 5 doesn't divide m (otherwise from #3, 5 woud divide m' which from #8 it does not)
(10) From #7, we know that 5 divides u (since it divides 4b, n't but doesn't divide m')
(11) We also know that t = ± 2 since u = 0 and (t + u√5)/2 is a unit.
(12) From #11, we know that a + b√5 = ± [(m + n√5)/2]5
(13) From #12 and Lemma 1 above and the fact that m ≡ n (mod 2), we can conclude that m,n are even.
(14) Let:
c = ±m/2
d = ±n/2
(15) a + b√5 = ±(c + d√5)5 = c5 + 5c4d√5 + 50c3d2 + 50c2d3√5 + 125cd4 + 25d5√5.
(16) So:
a = c5 + 50c3c2 + 125cd4 = c(c4 + 50c2d2 + 125d4)
b = 5c4d + 50c2d3 + 25d5 = 5d(c4 + 10c2d2 + 5d4)
(17) gcd(c,d) = 1 since c divides a, d divides b. If gcd(c,d) ≠ 1 then it would mean a,b have a common factor which they don't.
(18) c,d have different parities
(a) c,d cannot both be even since gcd(c,d)=1 from #17
(b) c,d cannot both be odd since from #16:
a = odd(odd + even + odd) = odd(even) = even
b = odd(odd + even + odd) = odd(even) = even
Which is impossible since a,b have different parities.
(c) Therefore c,d have different parities too.
(19) 5 doesn't divide c since 5 doesn't divide m from #9.
(20) Finally, we know that c,d are nonzero since:
(a) c is nonzero from #16 since a is nonzero
(b) d is nonzero from #16 since b is nonzero
QED
Lemma 3: Given a,b such that:
(a) gcd(a,b)=1
(b) a,b have different parities (one is odd, one is even)
(c) a,b are nonzero
(d) 5 doesn't divide a
(e) 5 divides b
(f) a + b√5 = [(m + n√5)/2]5([t+u√5]/2) where u ≠ 0.
Then:
(a) a = c(c4 + 50c2d2 + 125d4)
(b) b = 5d(c4 + 10c2d2 + 5d4)
(c) gcd(c,d)=1
(d) c,d have different parities
(e) 5 doesn't divide c
(f) c,d are nonzero
Proof:
(1) Since [t+u√5]/2 is a unit, we know that there exists an integer e (see here) such that:
[t+u√5]/2 = ±([1 + √5]/2)e
(2) By our assumption that u ≠ 0, we know that e ≠ 0
(3) We can assume that e is positive, since we make e positive by replacing [1 + √5]/2 with its inverse -(1 - √5)/2 since:
(a) [(1 + √5)/2]-1 = 2/(1 + √5) = 2(1 - √5)/(1 - 5) = (2 - 2√5)/(-4) = (1 - √5)/(-2) = -(1 - √5)/2
(b) [(1 + √5)/2]-e = ([(1 + √5)/2]-1)e = [-(1 - √5)/2 ]e
(4) We know that e is ≥ 2 since:
(a) Since 5 divides b, it must divide u (see the reasoning in lemma 2)
(b) But if e = 1, then u = ±1 which is not divisible by 5.
(5) So, we can assume that (t + u√5)/2 = [±(1 √5)e]/(2e)
(6) Which implies that:
±(2e-1)(t + u√5) = (1 ± √5)e
(7) Using the binomial theorem (see here), we see that 2e-1u ≡ ±e (mod 5) since:
(1 ± √5)e = 1 + e√5 + [e*(e-1)]5 + [e*(e-1)(e-2)](5)√5 + ... + (√5)e
Since e ≥ 2, we know that all other value but the second one are divisible by 5.
(8) Since 5 divides u (from #4a), we know that e ≡ 0 (mod 5) so that 5 divides e.
(9) Then there must exist f such that e = 5f.
(10) We can assume that there exist c',d' such that:
(c' + d'√5)/2 = [(m + n√5)/2][(1 ± √5)/2]f
(11) From this we know that:
a + b√5 = [(c' + d'√5)/2]
(12) We further know that c', d' have the same parity (because of the nature of Z[(1 + √5)/2]) so that we can assume that they are even from Lemma 1 above.
(13) This allows us to suppose there c,d such that:
c = ±c'/2, d = ±d'/2
(14) We now have the equation:
a + b√5 = ±(c + d√5)5
(15) This allows to follow the same logic from Lemma 2, starting at step #15.
QED
Sunday, January 15, 2006
Saturday, January 14, 2006
Discriminants and Reduced Equations
In today's blog, I will go over some lemmas that are needed to complete the solution to Pell's Equation using purely periodic continued fractions.
The lemmas in today's proof is taken from Heinrich Dorrie's 100 Great Problems of Elementary Mathematics.
Lemma 1: Let D = 4n and let g = floor(√n). The coefficients for a reduced quadratic equation are: a = 1, b = -2g, c = g2 - n.
(1) The discriminant D = b2 - 4ac (see here for review)
(2) We know that r + b is less than 2a which is less than r - b since:
(a) 2√n - 2g is less than 2 [since we defined g as the floor of √n, we know that this value - g is less than 1.
(b) We also know that 2 is less than 2√n + 2g since √n + g is greater than 1.
(c) Since r = 2√n and since we are assuming that b = -2g, r + b = 2√n - 2g and likewise r - b = 2√n + 2g
(3) This proves tht we have a reduced fraction since:
-(r + b)/2a is a negative proper fraction
r - b/2a is a positive improper fraction.
QED
Lemma 2: Let D = 4n + 1. Let g be the largest integer for which g2 + g will be smaller than n [so that, (g + 1)2 + (g+1) is greater than n]. In this case, setting a = 1, b = -(2g + 1), c = g2 + g - n gives us a reduced quadratic equation.
(1) First, we note that √D - (2g + 1) is less than 2.
(a) From our assumption about g2 + g, we know that (g + 1)2 + (g+1) is greater than n and that:
(g+1)2 + g + 1 = g2 + 2g + 1 + g + 1 = g2 + 3g + 2
(b) Multiplying the above by 4 and adding 1 to each side gives us:
4g2 + 12g + 9 is greater than 4n + 1.
(c) So that we have:
(2g + 3)2 is greater than D.
(d) From this, it follows that 2g + 3 is greater than √D
(e) Rearranging this gives us:
√D - (2g + 1) is less than 2.
(2) 2 is less than √D + 2g + 1 since:
D ≥ 1 and g≥ 1.
(3) We then have r + b is less than 2a since:
r = √D and b = -(2g + 1)
(4) We also have 2a is less than r - b.
(5) So using the same reasoning in Lemma 1 we are done.
QED
The lemmas in today's proof is taken from Heinrich Dorrie's 100 Great Problems of Elementary Mathematics.
Lemma 1: Let D = 4n and let g = floor(√n). The coefficients for a reduced quadratic equation are: a = 1, b = -2g, c = g2 - n.
(1) The discriminant D = b2 - 4ac (see here for review)
(2) We know that r + b is less than 2a which is less than r - b since:
(a) 2√n - 2g is less than 2 [since we defined g as the floor of √n, we know that this value - g is less than 1.
(b) We also know that 2 is less than 2√n + 2g since √n + g is greater than 1.
(c) Since r = 2√n and since we are assuming that b = -2g, r + b = 2√n - 2g and likewise r - b = 2√n + 2g
(3) This proves tht we have a reduced fraction since:
-(r + b)/2a is a negative proper fraction
r - b/2a is a positive improper fraction.
QED
Lemma 2: Let D = 4n + 1. Let g be the largest integer for which g2 + g will be smaller than n [so that, (g + 1)2 + (g+1) is greater than n]. In this case, setting a = 1, b = -(2g + 1), c = g2 + g - n gives us a reduced quadratic equation.
(1) First, we note that √D - (2g + 1) is less than 2.
(a) From our assumption about g2 + g, we know that (g + 1)2 + (g+1) is greater than n and that:
(g+1)2 + g + 1 = g2 + 2g + 1 + g + 1 = g2 + 3g + 2
(b) Multiplying the above by 4 and adding 1 to each side gives us:
4g2 + 12g + 9 is greater than 4n + 1.
(c) So that we have:
(2g + 3)2 is greater than D.
(d) From this, it follows that 2g + 3 is greater than √D
(e) Rearranging this gives us:
√D - (2g + 1) is less than 2.
(2) 2 is less than √D + 2g + 1 since:
D ≥ 1 and g≥ 1.
(3) We then have r + b is less than 2a since:
r = √D and b = -(2g + 1)
(4) We also have 2a is less than r - b.
(5) So using the same reasoning in Lemma 1 we are done.
QED
Tuesday, January 10, 2006
Pell's Equation: The Solution with Reduced Quadratic Equations
In a previous blog, I showed how combining 2x2 matrices with continued fractions can lead to a solution to Pell's Equation (see here).
In today's blog, I will show a solution that uses purely periodic continued fractions. Most of today's proof is based on Heinrich Dorrie's: 100 Great Problems of Elementary Mathematics.
The important idea in today's solution is the two concepts purely periodic continued fractions and reduced quadratic equations.
A purely periodic continued fraction is a continued fraction where the entire continued fraction is repeated. In other words, the continued fraction has this form: [a0, a1, ..., an-1 ].
A periodic continued fraction is not purely periodic if not all the elements repeat. For example, the following periodic continued fraction is not purely periodic: [ a0, a1, a2, ..., an-1 ].
A reduced quadratic equation is a quadratic equation that has relatively prime, integer coefficients, a squarefree discriminant, a first root which is a positive, improper fraction, and a second root which is a negative, proper fraction. (See here for details)
We start with a lemma that will be needed in the solution.
Lemma 1: if there exists two different quadratic equations with the same solution such that we have:
(a) au2 + bu + c = 0, gcd(a,b,c)=1, a,b,c are integers
(b) a'u2 + b'u + c' = 0, a' ≠ a, b' ≠ b, c' ≠ c, and a', b', c' integers
Then, there exists an integer y such that y = a'/a = b'/b = c'/c.
(1) Let y = c'/c so that c' = cy
(2) From (a), we know that -c/u = au + b since:
-c = au2 + bu = u(au + b)
(3) From (b), we know that -c'/u = a'u + b' for the same reason.
(4) From (1) and (3), we have -cy/u = a'u + b' which gives us:
-c/u = (a'u + b')/y = a'u/y + b'/y
(5) Applying (4) with (2) gives us:
au + b = -c/u = a'u/y + b'/y
(6) One possible solution to (5) is to assume:
au = a'u/y
b = b'/y
(7) Combining (6) with (1) gives us:
c'/c = a'/a = b'/b = y
(8) Now, we need to show that y is an integer.
(9) Assume that y is not an integer.
(10) Then there exist integers u,v such that gcd(u,v)=1 and y=u/v
We can assume that gcd(u,v)=1 since if it is not, we can factor out any common primes.
(11) From (9), we can assume that v ≠ 1.
(12) So u/v = c'/c = a'/a = b'/b
(13) So c'v = cu which implies that v divides c (since gcd(u,v)=1).
(14) And b'v = bu implies that v divides b
(15) But gcd(b,c)=1 (from our assumption) so we have a contradiction and we can reject #9.
QED
Theorem 1: A reduced quadratic equation can be used to solve x2 - dy2 = 4
(1) Let [ a1, a2, ... an, a1, ... an ] be the representation of a reduced quadratic equation au2 + bu + c = 0 where n is the period and whose discriminant D = d. [See here for proof that a reduced quadratic equation results in a purely periodic continued fraction]
(2) Let N is be an even multiple of n. For purposes of this proof, we can assume that N = 2n.
(3) Let P/Q = [ a1, ... an ... aN ]
(4) Let p/q = [ a1, ... an ... aN-1 ]
(5) From a previous result and (1) we know that;
u = (Pu + p)/(Qu + q) [see here]
So that:
Qu2 + qu - Pu - p = 0
(6) Let H = P - q
(7) We then have the following form for (5)
Qu2 - Hu - p = 0
(8) From the lemma above, we know that there exists y such that:
y = Q/a = P-q/-b = p/-c
(9) We can also define a value x such that x = P + q
(10) From (8), -by = P-q
(11) Combining (9) and (10) gives us:
x2 - b2y2 = (P + q)2 - (P-q)2
(12) From (8):
4acy2 = 4ac(Q/a)(p/-c) = -4Qp
(13) Since D = b2 - 4ac, we have:
x2 - dy2 = x2 - Dy2 =
= x2 - (b2 - 4ac)y2 =
= x2 - b2y2 + 4acy2
(14) Combining (13) with (11) and (12) gives us:
x2 - dy2 = (P + q)2 - (P - q)2 - 4Qp =
= 4Pq - 4Qp = 4(Pq - Qp)
(15) We know that Pq - Qp = 1 (see Step #4 in Theorem 2 below), so that we have now proven that using a reduced equation of D = d gives us:
x2 - dy2 = 4(Pq - Qp) = 4(1) = 4
QED
Corrolary 1.1: This equation can be used to solve Pell's Equation
(1) Pell's equation refers to the equation: x2 - dy2 = 1.
(2) Let x' = 2x, d' = 4d.
(3) Use the above theorem to solve:
(x')2 - (d')y2 = 4
This means that:
(2x)2 - (4d)y2 =4x2 - 4dy2 = 4
Which dividing all sides by 4 implies:
x2 - dy2 = 1.
QED
Theorem 2: Every solution to the equation x2 - dy2 = 4 is solved by the method in Thereom 1.
(1) Let x, y be a solution to x2 - dy2 = 4.
(2) We know that there exists a reduced quadratic equation that has a discriminant = D (see here for proof) such that:
au2 + bu + c = 0.
(3) We can define four values: P,Q,p,q such that:
P = (x - by)/2
Q = ay
p = -cy
q = (x + by)/2
(4) We note that Pq - Qp = 1 since
(x-by)/2 * (x+by)/2 - (ay)(-cy) = [x2 - b2y2]/4 + acy2 =
= [x2 - b2y2 + 4acy2]/4 =
= [x2 - (b2 - 4ac)y2]/4 =
= [x2 - dy2]/4
(5) Now applying #1 to #4 gives us:
Pq - Qp = [x2 - dy2]/4 = 4/4 = 1
(6) From #3, we have:
a = Q/y [from Q=ay]
b = -(P-q)/y [from q-P = (x + by)/2 - (x-by)/2 = 2by/2 = by --> b = -(P-q)/y]
c = -p/y [from p=-cy]
(7) Applying this to #2 gives us:
(Q/y)u2 + [-(P-q)/y]u + -p/y = 0
(8) Multiplying all sides by y gives us:
Qu2 -Pu + qu -p = 0
(9) Which implies:
Qu2 + qu = Pu + p
(10) And then:
u = (Pu + p)/(Qu + q)
(11) Finally we, prove that Q ≥ q
(a) From #3, we know that
2(Q - q) = 2(ay - [x + by]/2) = 2ay - x -by = [2a - b]y - x
(b) Since the second root of #2 is a negative proper fraction (see here for definition of reduced quadratic equation), we have:
-(-r -b) is less than 2a which implies that r + b is less than 2a and that 2a - b is greater than r.
(c) Since r2 = d (see here for definition of discriminant) and using #1, we get:
r2y2 - x2 = -1(x2 - dy2) = -4
(d) So:
2(Q -q) is greater than ry - x = (r2y2 - x2)/(ry+x) = -4/(ry + x) which simplifies to: (Q - q) is greater than -2/(ry + x)
(e) We know that D is a squarefree, positive integer so D ≥ 2 so r is greater than 1.
(f) We know that y is at least 1 (since we are ignoring the trivial solution: x=2,y=0). We know that x is at least 3 since it must be greater than √2*1 + 4 which means that x ≥ 3.
(g) This gives us Q - q is greater than -2/(2+3) = -2/(5) = -0.4. That is Q ≥ q (since Q is an integer and q is an improper fraction over 2).
(12) Since P/Q is a rational number, we can represent it as a finite continued fraction (see here) and we can assume that n is even (see Lemma 3 here)
Let's say P/Q = [ a1, a2, ..., an ]
(13) Let p'/q' be the approximation that comes just before P/Q.
(14) Then Pq' - Qp' = 1. [See here for details]
(15) If we subtract #5 from #14, we get:
Pq' - Qp' - (Pq - Qp) = P(q' - q) - Q(p' - p) = 1 - 1 = 0
(16) This implies that:
P(q' - q) = Q(p' - p).
(17) Since gcd(P,Q)=1 (see Lemma 6 here), since q ≤ Q (see #11) and q' is less than Q (see here), then:
q' = q (since Q ≥ q' and Q divides q' - q) and since Q ≠ 0, p' = p.
(18) From all this we can conclude that:
[ a1, ..., an, u ] = (Pu + p)/(Qu + q) [ See here for proof ]
(19) Apply #10 gives us;
u = [ a1, ..., an, u ]
(20) Hence, as we can see each value x,y can in this way be gotten from the expansion of the reduced number u.
QED
Finally, I present an example that shows this method in action.
Example: Find the smallest solution for x2 - 112y2 = 4.
(1) We first find a reduced quadratic equation where the discriminant = 112. Let's use:
3u2 - 10u - 1 = 0.
D = b2 - 4ac = (-10)2 - 4(3)(-1) = 100 + 12 = 112
(2) We generate the continued fraction for this equation (see here for method):
u = [ 3, 2, 3, 10, ... ]
(3) In this case the period length is 4 so we take the first four approximate fractions (see here for method):
p1 = 3
p2 = 7
p3 = 24
p4 = 247
q1 = 1
q2 = 2
q3 = 7
q4 = 72
x = P + q = 247 + 7 = 254
y = Q/a = 72/3 = 24.
(254)2 - 112(24)2 = 64,516 - 112(576) = 64,516 - 64,512 = 4.
QED
In today's blog, I will show a solution that uses purely periodic continued fractions. Most of today's proof is based on Heinrich Dorrie's: 100 Great Problems of Elementary Mathematics.
The important idea in today's solution is the two concepts purely periodic continued fractions and reduced quadratic equations.
A purely periodic continued fraction is a continued fraction where the entire continued fraction is repeated. In other words, the continued fraction has this form: [a0, a1, ..., an-1 ].
A periodic continued fraction is not purely periodic if not all the elements repeat. For example, the following periodic continued fraction is not purely periodic: [ a0, a1, a2, ..., an-1 ].
A reduced quadratic equation is a quadratic equation that has relatively prime, integer coefficients, a squarefree discriminant, a first root which is a positive, improper fraction, and a second root which is a negative, proper fraction. (See here for details)
We start with a lemma that will be needed in the solution.
Lemma 1: if there exists two different quadratic equations with the same solution such that we have:
(a) au2 + bu + c = 0, gcd(a,b,c)=1, a,b,c are integers
(b) a'u2 + b'u + c' = 0, a' ≠ a, b' ≠ b, c' ≠ c, and a', b', c' integers
Then, there exists an integer y such that y = a'/a = b'/b = c'/c.
(1) Let y = c'/c so that c' = cy
(2) From (a), we know that -c/u = au + b since:
-c = au2 + bu = u(au + b)
(3) From (b), we know that -c'/u = a'u + b' for the same reason.
(4) From (1) and (3), we have -cy/u = a'u + b' which gives us:
-c/u = (a'u + b')/y = a'u/y + b'/y
(5) Applying (4) with (2) gives us:
au + b = -c/u = a'u/y + b'/y
(6) One possible solution to (5) is to assume:
au = a'u/y
b = b'/y
(7) Combining (6) with (1) gives us:
c'/c = a'/a = b'/b = y
(8) Now, we need to show that y is an integer.
(9) Assume that y is not an integer.
(10) Then there exist integers u,v such that gcd(u,v)=1 and y=u/v
We can assume that gcd(u,v)=1 since if it is not, we can factor out any common primes.
(11) From (9), we can assume that v ≠ 1.
(12) So u/v = c'/c = a'/a = b'/b
(13) So c'v = cu which implies that v divides c (since gcd(u,v)=1).
(14) And b'v = bu implies that v divides b
(15) But gcd(b,c)=1 (from our assumption) so we have a contradiction and we can reject #9.
QED
Theorem 1: A reduced quadratic equation can be used to solve x2 - dy2 = 4
(1) Let [ a1, a2, ... an, a1, ... an ] be the representation of a reduced quadratic equation au2 + bu + c = 0 where n is the period and whose discriminant D = d. [See here for proof that a reduced quadratic equation results in a purely periodic continued fraction]
(2) Let N is be an even multiple of n. For purposes of this proof, we can assume that N = 2n.
(3) Let P/Q = [ a1, ... an ... aN ]
(4) Let p/q = [ a1, ... an ... aN-1 ]
(5) From a previous result and (1) we know that;
u = (Pu + p)/(Qu + q) [see here]
So that:
Qu2 + qu - Pu - p = 0
(6) Let H = P - q
(7) We then have the following form for (5)
Qu2 - Hu - p = 0
(8) From the lemma above, we know that there exists y such that:
y = Q/a = P-q/-b = p/-c
(9) We can also define a value x such that x = P + q
(10) From (8), -by = P-q
(11) Combining (9) and (10) gives us:
x2 - b2y2 = (P + q)2 - (P-q)2
(12) From (8):
4acy2 = 4ac(Q/a)(p/-c) = -4Qp
(13) Since D = b2 - 4ac, we have:
x2 - dy2 = x2 - Dy2 =
= x2 - (b2 - 4ac)y2 =
= x2 - b2y2 + 4acy2
(14) Combining (13) with (11) and (12) gives us:
x2 - dy2 = (P + q)2 - (P - q)2 - 4Qp =
= 4Pq - 4Qp = 4(Pq - Qp)
(15) We know that Pq - Qp = 1 (see Step #4 in Theorem 2 below), so that we have now proven that using a reduced equation of D = d gives us:
x2 - dy2 = 4(Pq - Qp) = 4(1) = 4
QED
Corrolary 1.1: This equation can be used to solve Pell's Equation
(1) Pell's equation refers to the equation: x2 - dy2 = 1.
(2) Let x' = 2x, d' = 4d.
(3) Use the above theorem to solve:
(x')2 - (d')y2 = 4
This means that:
(2x)2 - (4d)y2 =4x2 - 4dy2 = 4
Which dividing all sides by 4 implies:
x2 - dy2 = 1.
QED
Theorem 2: Every solution to the equation x2 - dy2 = 4 is solved by the method in Thereom 1.
(1) Let x, y be a solution to x2 - dy2 = 4.
(2) We know that there exists a reduced quadratic equation that has a discriminant = D (see here for proof) such that:
au2 + bu + c = 0.
(3) We can define four values: P,Q,p,q such that:
P = (x - by)/2
Q = ay
p = -cy
q = (x + by)/2
(4) We note that Pq - Qp = 1 since
(x-by)/2 * (x+by)/2 - (ay)(-cy) = [x2 - b2y2]/4 + acy2 =
= [x2 - b2y2 + 4acy2]/4 =
= [x2 - (b2 - 4ac)y2]/4 =
= [x2 - dy2]/4
(5) Now applying #1 to #4 gives us:
Pq - Qp = [x2 - dy2]/4 = 4/4 = 1
(6) From #3, we have:
a = Q/y [from Q=ay]
b = -(P-q)/y [from q-P = (x + by)/2 - (x-by)/2 = 2by/2 = by --> b = -(P-q)/y]
c = -p/y [from p=-cy]
(7) Applying this to #2 gives us:
(Q/y)u2 + [-(P-q)/y]u + -p/y = 0
(8) Multiplying all sides by y gives us:
Qu2 -Pu + qu -p = 0
(9) Which implies:
Qu2 + qu = Pu + p
(10) And then:
u = (Pu + p)/(Qu + q)
(11) Finally we, prove that Q ≥ q
(a) From #3, we know that
2(Q - q) = 2(ay - [x + by]/2) = 2ay - x -by = [2a - b]y - x
(b) Since the second root of #2 is a negative proper fraction (see here for definition of reduced quadratic equation), we have:
-(-r -b) is less than 2a which implies that r + b is less than 2a and that 2a - b is greater than r.
(c) Since r2 = d (see here for definition of discriminant) and using #1, we get:
r2y2 - x2 = -1(x2 - dy2) = -4
(d) So:
2(Q -q) is greater than ry - x = (r2y2 - x2)/(ry+x) = -4/(ry + x) which simplifies to: (Q - q) is greater than -2/(ry + x)
(e) We know that D is a squarefree, positive integer so D ≥ 2 so r is greater than 1.
(f) We know that y is at least 1 (since we are ignoring the trivial solution: x=2,y=0). We know that x is at least 3 since it must be greater than √2*1 + 4 which means that x ≥ 3.
(g) This gives us Q - q is greater than -2/(2+3) = -2/(5) = -0.4. That is Q ≥ q (since Q is an integer and q is an improper fraction over 2).
(12) Since P/Q is a rational number, we can represent it as a finite continued fraction (see here) and we can assume that n is even (see Lemma 3 here)
Let's say P/Q = [ a1, a2, ..., an ]
(13) Let p'/q' be the approximation that comes just before P/Q.
(14) Then Pq' - Qp' = 1. [See here for details]
(15) If we subtract #5 from #14, we get:
Pq' - Qp' - (Pq - Qp) = P(q' - q) - Q(p' - p) = 1 - 1 = 0
(16) This implies that:
P(q' - q) = Q(p' - p).
(17) Since gcd(P,Q)=1 (see Lemma 6 here), since q ≤ Q (see #11) and q' is less than Q (see here), then:
q' = q (since Q ≥ q' and Q divides q' - q) and since Q ≠ 0, p' = p.
(18) From all this we can conclude that:
[ a1, ..., an, u ] = (Pu + p)/(Qu + q) [ See here for proof ]
(19) Apply #10 gives us;
u = [ a1, ..., an, u ]
(20) Hence, as we can see each value x,y can in this way be gotten from the expansion of the reduced number u.
QED
Finally, I present an example that shows this method in action.
Example: Find the smallest solution for x2 - 112y2 = 4.
(1) We first find a reduced quadratic equation where the discriminant = 112. Let's use:
3u2 - 10u - 1 = 0.
D = b2 - 4ac = (-10)2 - 4(3)(-1) = 100 + 12 = 112
(2) We generate the continued fraction for this equation (see here for method):
u = [ 3, 2, 3, 10, ... ]
(3) In this case the period length is 4 so we take the first four approximate fractions (see here for method):
p1 = 3
p2 = 7
p3 = 24
p4 = 247
q1 = 1
q2 = 2
q3 = 7
q4 = 72
x = P + q = 247 + 7 = 254
y = Q/a = 72/3 = 24.
(254)2 - 112(24)2 = 64,516 - 112(576) = 64,516 - 64,512 = 4.
QED
Sunday, January 08, 2006
Continued Fractions: Purely Periodic Continued Fractions
In a previous blog, I showed a solution to Pell's Equation using continued fractions and matrices. One might reasonably ask if there is a simpler solution. It turns out that if we use the concept of purely periodic continued fractions, we can solve Pell's Equation using continued fractions but without needing to use matrix theory.
For those not familiar with continued fractions, start here. For those who are not familiar with Pell's Equation, start here. For those not familiar with how Pell's Equation fits into Fermat's Last Theorem, see here.
Today's blog is based on Heinrich Dorrie's 100 Great Problems of Elementary Mathematics.
In a previous blog, I showed that a continued fraction is periodic if and only if it represents the root of a quadratic equation (see here).
A purely periodic continued fraction is a continued fraction where the entire fraction a0 through an repeats. Here are some examples:
(a) This continued fraction is periodic but not purely periodic.
√6 = [ 2, 2, 4 ] (see here)
(b) This continued fraction is purely periodic.
√112 + 10/ 6 = [ 3, 2, 3, 10 ]
Just as periodic continued fractions correspond to quadratic equations, it turns out that purely periodic continued fractions correspond to what we will call "reduced" quadratic equations.
Definition: A reduced quadratic equation is any quadratic equation where the first root is a positive irrational greater than 1, its second root is a negative irrational that is greater than -1 and less than 0, and the discriminant is a nonsquare integer.
The discriminant refers to D in the following equation (see here):
x = (-b ± √d)/2a =(-b ± √b2 - 4ac)/2a
So the discriminant D is always equal to: b2 - 4ac.
In other words, the first root is a positive improper fraction (a fraction whose numerator is larger than or equal to its denominator such as 11/4 or 3/3) and the second root is a negative proper fraction (a fraction whose numerator is less than its denominator such as 1/2 or 1/3).
In my next blog, I will show how purely periodic continued fractions can be used to solve Pell's Equation.
Lemma 1: Every purely periodic continued fraction is a representation of a reduced quadratic equation.
(1) Let α be the purely periodic continued fraction with period n:
α = [ a1, a2, ...., an, a1, ... ]
(2) Let N be an even multiple of n such that we have:
α = [ a1, a2,, ..., aN, α ]
(3) We can assume that a1, a2, ... are integers greater than 0. [See here]
(4) Let P/Q be the Nth approximation of this continued fraction such that:
P/Q = [ a1, a2, ..., aN ]
(5) Let p/q be the (N-1)th approximation of this continued fraction such that:
p/q = [ a1, a2, ..., aN-1 ]
(6) According to previous results:
(a) Pq - Qp = 1 (see Lemma 2 here)
(b) α = (Pα + p)/(Qα + q) (see Lemma 1 here)
(c) α lies in between P/Q and p/q. It is greater than one and less than the other. (see Corollary 5.2 here )
(7) Rearranging (6b) gives us:
Qα2 + qα - Pα - p = 0.
(8) If we set H = P - q, we get:
Qα2 - Hα - p = 0.
(9) Solving for α gives us two roots such that:
α = H ± √H2 + 4Qp/(2Q)
(10) The discriminant D = H2 + 4Qp (see definition above) which means:
D = H2 + 4Pq - 4 = (P + q)2 - 4.
This shows that D is not a square (see here for proof )
(11) Let r = √D
(12) If we set α as the first root and α as the second root, we see that:
α = (H + r)/2Q
α = (H - r)/2Q
(13) We also note that r is greater than H since r = H2 + 4Qp and 4Qp ≥ 4 (see here)
(14) So we know that α is positive and that α is negative (since r,Q are ≥ 1; Q is greater than 1 by above)
(15) We know that α is an improper fraction since in order for it to repeat, it needs to be equal to the reciprocal of a proper fraction (that is, 1/[α - floor(α)] ) so that all we have left is to prove that α is a proper fraction.
(16) α * α = (H+r)(H-r)/[(2Q)(2Q)] = H2 - r2/4Q2 =
=( H2 - [H2 + 4Qp])/4Q2 =
-4Qp/4Q2 = -p/Q
(17) So α = (p/Q)/α
(18) Since P is greater than p (see Corollary 4.2, here), Q is greater than q (see Lemma 4 here), we have:
- α is less than (P/Q)/α and less than (p/q)/α
(19) But since α lies between P/Q and p/q (see #6c above), we know that one value is greater than α and one value is less than α.
(20) A value less over α is a proper fraction and we have shown that - α lies between 0 and a proper fraction. So, therefore, it must be a proper fraction.
(21) We have thus proven that α is a reduced number -- that is, it is the root a reduced equation (see definition above)
QED
Lemma 2: All irrational numbers that result from the continued fraction expansion of a reduced number are themselves solutions to a quadratic equation.
(1) Let α be a reduced number.
That is, it is an improper fraction solution to:
ax2 + bx + c = 0
Where: a,b,c are relatively prime integers and α is a negative proper fraction.
(2) For the start of the expansion, we note that:
α' = 1/(α - g)
That is: g is the largest whole number less than α and α' is the first derivative from α. In this case, g corresponds to a0 of the continued fraction.
(3) Let's also define a', b', c' such that:
a' = -ag2 - bg - c
b' = -2ag - b
c' = -a
We see in each of these cases that a',b', and c' are integers.
(4) Let D = the discriminant = b2 - 4ac
(5) Let r = √D so that:
α = (-b + r)/2a
α = (-b - r)/2a
(6) From #2 and #3, we have:
α' = 1/(α - g) = 1/[(r-b)/2a - g] = 1/[(r - b - 2ag)/2a] = 2a/(r - b - 2ag) = 2a/(r + b')
(7) We can continue working with 2a/(r + b') to get:
2a/(r + b') = [2a(r - b')]/(r2 - b'2)
(8) r2 - b'2 = b2 - 4ac - (-2ag - b)2 =
= b2 - 4ac - 4a2g2 - 4abg - b2 =
= 2a(-2c - 2ag2 -2bg) =
= (2a)(2)(-c + -ag2 - bg) = (2a)(2a')
(9) Combining #7 and #8 gives us:
α' = 2a/(r + b') = (r - b')/(2a')
(10) Further, we note that:
b'2 - 4a'c' = (-2ag - b)2 - 4(-ag2 - bg - c)(-a) =
= 4a2g2 + 4abg + b2 -4a2g2 - 4abg - 4ac = b2 - 4ac
(11) So that r = √b2 - 4ac = √b'2 - 4a'c'
(12) Putting together #9 and #11, gives us:
α' = [-b' + √b'2 - 4a'c']/(2a')
(13) And this is a solution to a quadratic equation (see here) which gives us:
a'α2 + b'α' + c' = 0.
(14) We know that α' is a positive, improper fraction since:
α' = 1/(α - g) and α - g is less than 1.
(15) Further, we can use the same reasoning to establish that:
α' = 1/(α - g) is the second solution to the same equation since:
α = (-b-r)/2a
1/(α - g) = 1/[(-b-r-2ag)/2a] = 2a/(-b -r -2ag) = 2a/(-r + b') = 2a(-r -b')/(r2 - b'2)
Combining the above with #8 gives:
α' = (-r -b')/2a'
(16) By the equation in #15, we can also see that:
α' is a negative proper fraction since g is an integer greater than 1.
QED
Lemma 3: If α is a reduced number, then its continued fraction representation is purely periodic.
(1) Let α be a reduced number. That is:
(a) α is a positive, improper fraction of an integral quadratic equation such that:
aα2 + bα + c = 0.
(b) α is the second root for the above equation and is a negative, proper fraction.
(c) The discriminant: D = b2 - 4ac and is not a square.
(2) α * α =
(b2 - b2 + 4ac)/4a2 = c/a
(3) α + α =
= -2b/2a = -b/a
(4) From #2 and #3, we can assume that c,b are negative and a is positive.
We know that product is negative and we know that the addition is positive since α is greater than α
(5) For a continued fraction, we know that:
α = g + 1/α'
We know that g is the greatest integer less than α.
We also know that α' is itself a reduced number.
(6) From lemma 2, we also know that:
α' = 1/(α - g)
1/α' = α - g
-1/α' = g - α
(7) As shown in Lemma 2, each reduced number in the continued fraction representation corresponds to the same discriminant D (see Lemma 2 above)
(8) The number of different reduced numbers that correspond to a given discriminant D is finite since:
(a) -ac is greater than 0 since a is positive and c is negative.
(b) We know that b is negative so that b can only take value -1, -2, ... -r since b2 - 4ac must equal D.
(c) Additionally since D is nonsquare, we know that ac ≥ 1 and we know that b2 must then be divisible by 4.
(d) From (c), we know that -ac = (D - b2)/4 which in turn gives us a finite amount of numbers a,c since for each (D - b2)/4 value there are only so many integers than when multiplied are equal to this result: a can take value from 1 thru (D - b2)/4 and c can take a value from -1 thru -(D - b2)/4 value.
(9) From #8, we know that there are a finite number of derived values (α') that can come up so eventually the continued fraction will repeat.
(10) So, let's assume that we have a pattern that repeats:
U = (K, L, u)
u = (h,k,l,u)
In the above case, u is the irrational number that repeats. K,L,h,k,l are integers.
(11) We know that the solution u is associated with a second root u
(12) Now, according to #6, we know that for the same second root, there must be the same previous floor value. So, we can conclude that L=l and K=k.
(13) In other words, all previous values of the continued fraction must match.
(14) The only way that this can work is if we are dealing with a purely periodic continued fraction.
Since, #13 is not true of a repeating continued fraction that is not a purely periodic continued fraction:
Consider √6 above, sometimes the value preceding the 2 is a 2 and sometimes it is a 4. In other words, it violates the assumption in #13.
On the other hand, this is true of a purely periodic continued fraction.
Consider √112 + 10/ 6 above, all integers will always have the same value beforehand the same value. It does not violate the assumption in #13.
QED
Theorem 1: An irrational number results in a purely periodic continued fraction if and only if it is a reduced number.
(1) All purely periodic continued fractions represent reduced numbers (Lemma 1)
(2) All reduced numbers result in purely periodic continued fractions (Lemma 3)
QED
For those not familiar with continued fractions, start here. For those who are not familiar with Pell's Equation, start here. For those not familiar with how Pell's Equation fits into Fermat's Last Theorem, see here.
Today's blog is based on Heinrich Dorrie's 100 Great Problems of Elementary Mathematics.
In a previous blog, I showed that a continued fraction is periodic if and only if it represents the root of a quadratic equation (see here).
A purely periodic continued fraction is a continued fraction where the entire fraction a0 through an repeats. Here are some examples:
(a) This continued fraction is periodic but not purely periodic.
√6 = [ 2, 2, 4 ] (see here)
(b) This continued fraction is purely periodic.
√112 + 10/ 6 = [ 3, 2, 3, 10 ]
Just as periodic continued fractions correspond to quadratic equations, it turns out that purely periodic continued fractions correspond to what we will call "reduced" quadratic equations.
Definition: A reduced quadratic equation is any quadratic equation where the first root is a positive irrational greater than 1, its second root is a negative irrational that is greater than -1 and less than 0, and the discriminant is a nonsquare integer.
The discriminant refers to D in the following equation (see here):
x = (-b ± √d)/2a =(-b ± √b2 - 4ac)/2a
So the discriminant D is always equal to: b2 - 4ac.
In other words, the first root is a positive improper fraction (a fraction whose numerator is larger than or equal to its denominator such as 11/4 or 3/3) and the second root is a negative proper fraction (a fraction whose numerator is less than its denominator such as 1/2 or 1/3).
In my next blog, I will show how purely periodic continued fractions can be used to solve Pell's Equation.
Lemma 1: Every purely periodic continued fraction is a representation of a reduced quadratic equation.
(1) Let α be the purely periodic continued fraction with period n:
α = [ a1, a2, ...., an, a1, ... ]
(2) Let N be an even multiple of n such that we have:
α = [ a1, a2,, ..., aN, α ]
(3) We can assume that a1, a2, ... are integers greater than 0. [See here]
(4) Let P/Q be the Nth approximation of this continued fraction such that:
P/Q = [ a1, a2, ..., aN ]
(5) Let p/q be the (N-1)th approximation of this continued fraction such that:
p/q = [ a1, a2, ..., aN-1 ]
(6) According to previous results:
(a) Pq - Qp = 1 (see Lemma 2 here)
(b) α = (Pα + p)/(Qα + q) (see Lemma 1 here)
(c) α lies in between P/Q and p/q. It is greater than one and less than the other. (see Corollary 5.2 here )
(7) Rearranging (6b) gives us:
Qα2 + qα - Pα - p = 0.
(8) If we set H = P - q, we get:
Qα2 - Hα - p = 0.
(9) Solving for α gives us two roots such that:
α = H ± √H2 + 4Qp/(2Q)
(10) The discriminant D = H2 + 4Qp (see definition above) which means:
D = H2 + 4Pq - 4 = (P + q)2 - 4.
This shows that D is not a square (see here for proof )
(11) Let r = √D
(12) If we set α as the first root and α as the second root, we see that:
α = (H + r)/2Q
α = (H - r)/2Q
(13) We also note that r is greater than H since r = H2 + 4Qp and 4Qp ≥ 4 (see here)
(14) So we know that α is positive and that α is negative (since r,Q are ≥ 1; Q is greater than 1 by above)
(15) We know that α is an improper fraction since in order for it to repeat, it needs to be equal to the reciprocal of a proper fraction (that is, 1/[α - floor(α)] ) so that all we have left is to prove that α is a proper fraction.
(16) α * α = (H+r)(H-r)/[(2Q)(2Q)] = H2 - r2/4Q2 =
=( H2 - [H2 + 4Qp])/4Q2 =
-4Qp/4Q2 = -p/Q
(17) So α = (p/Q)/α
(18) Since P is greater than p (see Corollary 4.2, here), Q is greater than q (see Lemma 4 here), we have:
- α is less than (P/Q)/α and less than (p/q)/α
(19) But since α lies between P/Q and p/q (see #6c above), we know that one value is greater than α and one value is less than α.
(20) A value less over α is a proper fraction and we have shown that - α lies between 0 and a proper fraction. So, therefore, it must be a proper fraction.
(21) We have thus proven that α is a reduced number -- that is, it is the root a reduced equation (see definition above)
QED
Lemma 2: All irrational numbers that result from the continued fraction expansion of a reduced number are themselves solutions to a quadratic equation.
(1) Let α be a reduced number.
That is, it is an improper fraction solution to:
ax2 + bx + c = 0
Where: a,b,c are relatively prime integers and α is a negative proper fraction.
(2) For the start of the expansion, we note that:
α' = 1/(α - g)
That is: g is the largest whole number less than α and α' is the first derivative from α. In this case, g corresponds to a0 of the continued fraction.
(3) Let's also define a', b', c' such that:
a' = -ag2 - bg - c
b' = -2ag - b
c' = -a
We see in each of these cases that a',b', and c' are integers.
(4) Let D = the discriminant = b2 - 4ac
(5) Let r = √D so that:
α = (-b + r)/2a
α = (-b - r)/2a
(6) From #2 and #3, we have:
α' = 1/(α - g) = 1/[(r-b)/2a - g] = 1/[(r - b - 2ag)/2a] = 2a/(r - b - 2ag) = 2a/(r + b')
(7) We can continue working with 2a/(r + b') to get:
2a/(r + b') = [2a(r - b')]/(r2 - b'2)
(8) r2 - b'2 = b2 - 4ac - (-2ag - b)2 =
= b2 - 4ac - 4a2g2 - 4abg - b2 =
= 2a(-2c - 2ag2 -2bg) =
= (2a)(2)(-c + -ag2 - bg) = (2a)(2a')
(9) Combining #7 and #8 gives us:
α' = 2a/(r + b') = (r - b')/(2a')
(10) Further, we note that:
b'2 - 4a'c' = (-2ag - b)2 - 4(-ag2 - bg - c)(-a) =
= 4a2g2 + 4abg + b2 -4a2g2 - 4abg - 4ac = b2 - 4ac
(11) So that r = √b2 - 4ac = √b'2 - 4a'c'
(12) Putting together #9 and #11, gives us:
α' = [-b' + √b'2 - 4a'c']/(2a')
(13) And this is a solution to a quadratic equation (see here) which gives us:
a'α2 + b'α' + c' = 0.
(14) We know that α' is a positive, improper fraction since:
α' = 1/(α - g) and α - g is less than 1.
(15) Further, we can use the same reasoning to establish that:
α' = 1/(α - g) is the second solution to the same equation since:
α = (-b-r)/2a
1/(α - g) = 1/[(-b-r-2ag)/2a] = 2a/(-b -r -2ag) = 2a/(-r + b') = 2a(-r -b')/(r2 - b'2)
Combining the above with #8 gives:
α' = (-r -b')/2a'
(16) By the equation in #15, we can also see that:
α' is a negative proper fraction since g is an integer greater than 1.
QED
Lemma 3: If α is a reduced number, then its continued fraction representation is purely periodic.
(1) Let α be a reduced number. That is:
(a) α is a positive, improper fraction of an integral quadratic equation such that:
aα2 + bα + c = 0.
(b) α is the second root for the above equation and is a negative, proper fraction.
(c) The discriminant: D = b2 - 4ac and is not a square.
(2) α * α =
(b2 - b2 + 4ac)/4a2 = c/a
(3) α + α =
= -2b/2a = -b/a
(4) From #2 and #3, we can assume that c,b are negative and a is positive.
We know that product is negative and we know that the addition is positive since α is greater than α
(5) For a continued fraction, we know that:
α = g + 1/α'
We know that g is the greatest integer less than α.
We also know that α' is itself a reduced number.
(6) From lemma 2, we also know that:
α' = 1/(α - g)
1/α' = α - g
-1/α' = g - α
(7) As shown in Lemma 2, each reduced number in the continued fraction representation corresponds to the same discriminant D (see Lemma 2 above)
(8) The number of different reduced numbers that correspond to a given discriminant D is finite since:
(a) -ac is greater than 0 since a is positive and c is negative.
(b) We know that b is negative so that b can only take value -1, -2, ... -r since b2 - 4ac must equal D.
(c) Additionally since D is nonsquare, we know that ac ≥ 1 and we know that b2 must then be divisible by 4.
(d) From (c), we know that -ac = (D - b2)/4 which in turn gives us a finite amount of numbers a,c since for each (D - b2)/4 value there are only so many integers than when multiplied are equal to this result: a can take value from 1 thru (D - b2)/4 and c can take a value from -1 thru -(D - b2)/4 value.
(9) From #8, we know that there are a finite number of derived values (α') that can come up so eventually the continued fraction will repeat.
(10) So, let's assume that we have a pattern that repeats:
U = (K, L, u)
u = (h,k,l,u)
In the above case, u is the irrational number that repeats. K,L,h,k,l are integers.
(11) We know that the solution u is associated with a second root u
(12) Now, according to #6, we know that for the same second root, there must be the same previous floor value. So, we can conclude that L=l and K=k.
(13) In other words, all previous values of the continued fraction must match.
(14) The only way that this can work is if we are dealing with a purely periodic continued fraction.
Since, #13 is not true of a repeating continued fraction that is not a purely periodic continued fraction:
Consider √6 above, sometimes the value preceding the 2 is a 2 and sometimes it is a 4. In other words, it violates the assumption in #13.
On the other hand, this is true of a purely periodic continued fraction.
Consider √112 + 10/ 6 above, all integers will always have the same value beforehand the same value. It does not violate the assumption in #13.
QED
Theorem 1: An irrational number results in a purely periodic continued fraction if and only if it is a reduced number.
(1) All purely periodic continued fractions represent reduced numbers (Lemma 1)
(2) All reduced numbers result in purely periodic continued fractions (Lemma 3)
QED
Wednesday, January 04, 2006
Continued Fractions and Matrices: More Lemmas
Today's blog continues exploring properties of continued fractions and matrices which are used in the solution for Pell's Equation. This blog assumes that you have already read the previous blog.
The details of today's blog is based on Harold M. Stark's An Introduction to Number Theory.
Lemma 1: if δ(1,√d) = (1,√d)Mn-1Mn+kj, then there exists rk, sk, tk, uk such that:
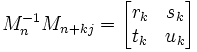
and
(dtk - sk) + (rk - uk)√d = 0.
(1) By assumption, we let:
δ(1,√d) = (1,√d)Mn-1Mn+kj [See here for an example where this assumption is true]
(2) Further, since we know that Mn-1 is a 2 x 2 matrix (see here), we know that the product with Mn+kj is a 2x2 matrix (see here) and we can assume that there exists rk, sk, tk, uk such that:
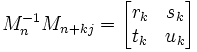
(3) Now, we know that:
δ(1,α) = (δ,δα) [See here for review of matrix math]
(4) From a previous result, we know that:
δ(1,α) = (1,α)Mn-1Mn+j [See here]
(5) Combining #4 and #5 with #2 gives us:
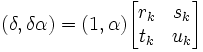
(6) From #6 (see here for review of matrix math), we can conclude that:
(δ, δα) = (rk+tkα, sk+ukα)
(7) This means that:
δ = rk + tkα
δα = sk + ukα
(8) Combining these two equations gives:
(rk + tkα)α = sk + ukα
(9) Which means that:
rkα + tkα2 = sk + ukα
(10) And subtracting the left-side value from both sides give us:
tkα2 + rkα - ukα - sk = 0
which is:
tkα2 + α(rk - uk) - sk = 0
(11) Since we know that α = √d (see here for review of α)
tkα2 + α(rk - uk) - sk = tkd +√d (rk - uk) - sk
(12) So, this gives us finally:
(dtk - sk) + (rk - uk)√d= 0.
QED
Lemma 2: Mn = Mm → n = m.
(1) Assume that Mn = Mm but n ≠ m
(2) Mn =
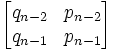
(3) Mm =
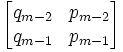
(4) Since Mn = Mm, we have:
qn-2 = qm-2
qn-1 = qm-1
(5) Now q1 is less than q2 and so on (see here for proof). So, m-2, n-2, n-1, m-1 must all be less than 1. (Otherwise, they cannot be equal)
(6) q0 and q-2 = 1 while q-1 = 0.
(7) So, m-2, n-2, n-1, m-1 cannot equal -1. [Since by #6 no other value = 0]
(8) On the other, it is possible for q-2 = q0 = q1 since all could = 1. (See here and here)
(9) So n-2, m-2, n-1, m-1 must equal -2,0, or 1.
(10) So n must = 2 (so that n-1 = 1, n-2 = 0). [Note: n=0 doesn't work since n-1 = -1; n=1 doesn't work since n-2=-1; and n=3 doesn't work since n-1 = 2]
(11) But then m must also = 2 (so that m-1=1, m-2=0) but this goes against our assumption.
(12) So we have a contradiction. There is no way that Mn = Mm without n = m.
QED
The details of today's blog is based on Harold M. Stark's An Introduction to Number Theory.
Lemma 1: if δ(1,√d) = (1,√d)Mn-1Mn+kj, then there exists rk, sk, tk, uk such that:
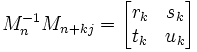
and
(dtk - sk) + (rk - uk)√d = 0.
(1) By assumption, we let:
δ(1,√d) = (1,√d)Mn-1Mn+kj [See here for an example where this assumption is true]
(2) Further, since we know that Mn-1 is a 2 x 2 matrix (see here), we know that the product with Mn+kj is a 2x2 matrix (see here) and we can assume that there exists rk, sk, tk, uk such that:
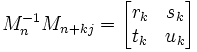
(3) Now, we know that:
δ(1,α) = (δ,δα) [See here for review of matrix math]
(4) From a previous result, we know that:
δ(1,α) = (1,α)Mn-1Mn+j [See here]
(5) Combining #4 and #5 with #2 gives us:
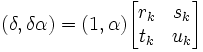
(6) From #6 (see here for review of matrix math), we can conclude that:
(δ, δα) = (rk+tkα, sk+ukα)
(7) This means that:
δ = rk + tkα
δα = sk + ukα
(8) Combining these two equations gives:
(rk + tkα)α = sk + ukα
(9) Which means that:
rkα + tkα2 = sk + ukα
(10) And subtracting the left-side value from both sides give us:
tkα2 + rkα - ukα - sk = 0
which is:
tkα2 + α(rk - uk) - sk = 0
(11) Since we know that α = √d (see here for review of α)
tkα2 + α(rk - uk) - sk = tkd +√d (rk - uk) - sk
(12) So, this gives us finally:
(dtk - sk) + (rk - uk)√d= 0.
QED
Lemma 2: Mn = Mm → n = m.
(1) Assume that Mn = Mm but n ≠ m
(2) Mn =
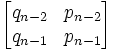
(3) Mm =
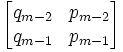
(4) Since Mn = Mm, we have:
qn-2 = qm-2
qn-1 = qm-1
(5) Now q1 is less than q2 and so on (see here for proof). So, m-2, n-2, n-1, m-1 must all be less than 1. (Otherwise, they cannot be equal)
(6) q0 and q-2 = 1 while q-1 = 0.
(7) So, m-2, n-2, n-1, m-1 cannot equal -1. [Since by #6 no other value = 0]
(8) On the other, it is possible for q-2 = q0 = q1 since all could = 1. (See here and here)
(9) So n-2, m-2, n-1, m-1 must equal -2,0, or 1.
(10) So n must = 2 (so that n-1 = 1, n-2 = 0). [Note: n=0 doesn't work since n-1 = -1; n=1 doesn't work since n-2=-1; and n=3 doesn't work since n-1 = 2]
(11) But then m must also = 2 (so that m-1=1, m-2=0) but this goes against our assumption.
(12) So we have a contradiction. There is no way that Mn = Mm without n = m.
QED
Continued Fractions and Matrices Continued
Today's blog continues a previous blog on how 2x2 matrices can be used to represent continued fractions. The lemmas presented in today's blog are used in the solution to Pell's Equation. For those interested in the background to Pell's Equation, start here. For those who would like to proceed to its solution using continued fractions and matrices, go here. The solution to Pell's Equation is used as part of the proof for Fermat's Last Theorem, n=5.
The content in today's blog is based on Harold M. Stark's An Introduction to Number Theory.
For Lemma 1, αn, qn are defined here. For Lemma 2, Mn is defined here.
Lemma 1: αnqn-1 + qn-2 ≠ 0
(1) Assume that αnqn-1 + qn-2 = 0.
(2) Then, qn-1 = 0 and qn-2 = 0. [See here for proof]
(3) But qn ≥ 1 for n ≥ 1. [See here]
(4) Futher, there are no successive 0's in a row since (see here for details on how these values are derived):
q-2 = 1
q-1=0
q0=1
(5) Therefore #2 is impossible and we reject our assumption.
QED
Lemma 2: if γn = αnqn-1 + qn-2, then γn(1,α) = (1,αn)Mn
(1) From the definition of Mn (see here), we know that:
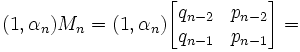
= (qn-2+αnqn-1, pn-2+αnpn-1) [See here for review on matrix products]
(2) By applying the equation α = (pn-2 + αnpn-1)/(qn-2 + αnqn-1) [See here], we get:
(qn-2+αnqn-1 , pn-2+αnpn-1) = (qn-2 + αnqn-1)(1,α)
(3) Adding back γn, this gives us:
(qn-2 + αnqn-1)(1,α) = γn(1,α)
QED
Lemma 3: if δ = γn+j/γn, then δ(1,√d) = (1,√d)Mn-1Mn+kj
(1) From Lemma 2, we know that;
γn(1 , α) = (1, αn)Mn
and
γn+j(1, α) = (1, αn+j)Mn+j
(2) By the definition of matrix inverses (see here), we know that:
(1,αn)MnMn-1 = (1,αn)
(3) From #1, then we have:
[(1,αn)Mn)] = γn(1,α)
(4) So, from #2, we have:
(1,αn) = γn(1,α)Mn-1
(5) Likewise since αn = αn+j (see here), we get:
(1,αn+j)Mn+j = (1,αn)Mn+j
(6) Applying #4, this gives us:
(1,αn+j)Mn+j = γn(1,α)Mn-1Mn+j
(7) Combining #1 with #6, gives us:
γn+j(1,α) = γn(1,α)Mn-1Mn+j
(8) Now, δ = γn+j/γn [We can do this since γn ≠ 0 (see Lemma 1 above) ]
(9) δ(1,α) = [(γn+j)(1 , α)]/γn
(10) Applying #7 gives us;
δ(1,α) = [γn(1,α)Mn-1Mn+j]/γn =
= (1,α)Mn-1Mn+j
QED
The content in today's blog is based on Harold M. Stark's An Introduction to Number Theory.
For Lemma 1, αn, qn are defined here. For Lemma 2, Mn is defined here.
Lemma 1: αnqn-1 + qn-2 ≠ 0
(1) Assume that αnqn-1 + qn-2 = 0.
(2) Then, qn-1 = 0 and qn-2 = 0. [See here for proof]
(3) But qn ≥ 1 for n ≥ 1. [See here]
(4) Futher, there are no successive 0's in a row since (see here for details on how these values are derived):
q-2 = 1
q-1=0
q0=1
(5) Therefore #2 is impossible and we reject our assumption.
QED
Lemma 2: if γn = αnqn-1 + qn-2, then γn(1,α) = (1,αn)Mn
(1) From the definition of Mn (see here), we know that:
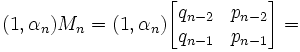
= (qn-2+αnqn-1, pn-2+αnpn-1) [See here for review on matrix products]
(2) By applying the equation α = (pn-2 + αnpn-1)/(qn-2 + αnqn-1) [See here], we get:
(qn-2+αnqn-1 , pn-2+αnpn-1) = (q
(3) Adding back γn, this gives us:
(q
QED
Lemma 3: if δ = γn+j/γn, then δ(1,√d) = (1,√d)Mn-1Mn+kj
(1) From Lemma 2, we know that;
γn(1 , α) = (1, αn)Mn
and
γn+j(1, α) = (1, αn+j)Mn+j
(2) By the definition of matrix inverses (see here), we know that:
(1,αn)MnMn-1 = (1,αn)
(3) From #1, then we have:
[(1,αn)Mn)] = γn(1,α)
(4) So, from #2, we have:
(1,αn) = γn(1,α)Mn-1
(5) Likewise since αn = αn+j (see here), we get:
(1,αn+j)Mn+j = (1,αn)Mn+j
(6) Applying #4, this gives us:
(1,αn+j)Mn+j = γn(1,α)Mn-1Mn+j
(7) Combining #1 with #6, gives us:
γn+j(1,α) = γn(1,α)Mn-1Mn+j
(8) Now, δ = γn+j/γn [We can do this since γn ≠ 0 (see Lemma 1 above) ]
(9) δ(1,α) = [(γn+j)(1 , α)]/γn
(10) Applying #7 gives us;
δ(1,α) = [γn(1,α)Mn-1Mn+j]/γn =
= (1,α)Mn-1Mn+j
QED
Saturday, December 31, 2005
Continued Fractions: Method for determining [ a0, a1, ... ]
Today's blog continues the discussion on Pell's Equation. For those interested in the background of this problem, start here. For those interested in understanding how this relates to Fermat's Last Theorem, start here.
In a previous blog, I explained how continued fractions can be used to solve Pell's Equation. In today's blog, I will go into more detail about a method for determining the representation of a continued fraction. This method is assumed in the solution to Pell's Equation which is found here.
Today's blog is based on the Jody Esmonde and M. Ram Murty's Problems in Algebraic Number Theory.
Theorem: For any irrational number α, it is possible to represent it in the form
[ a0, a1, ... ] where all values ai are integers and where we use the following equations:
(a) α0 = α
(b) ak = floor(αk)
(c) αk+1 = 1 / (αk - ak)
(1) First, I show this is true for the case k = 0.
α = α0 = floor(α0) + [α0 - floor(α0)] =
= a0 + 1/α1
(2) Assume it is true up to [a0, ..., αk]
(3) We see that:
αk = floor(αk) + [αk - floor(αk] =
= ak + 1/αk+1 =
[ a0, ..., ak, αk+1]
(4) By the Principle of Induction (see here), we are done.
QED
To show how this method can be used, let's apply it some examples:
Example 1: √6
a0 = floor(√6) = 2.
α1 = 1 / (√6 - 2) =
= (√6 + 2)/(6 - 4) =
= (√6 + 2)/2
a1 = floor([√6 + 2]/2) = 2
α2 = 1/[(√6 + 2)/2 - 2] =
= 1/[(√6 + 2 - 4)/2] =
= 1/[(√6 - 2)/2] =
= 2/(√6 - 2) =
= 2(√6 + 2)/(6 - 4) = 2(√6 + 2)/2 =
= √6 + 2
a2 = floor(√6 + 2) = 4.
α3 = 1/(√6 + 2 - 4) =
= 1/(√6 - 2) =
= (√6 + 2)/2
Since, this is the same as α1 so we have reached a repetition and we are done.
√6 = [ 2, 2, 4 ]
We note that:
n = 1 [Position where repetition begins is a1]
p = 2 [Size of period. The representation repeats every two items]
Example 2: √23
a0 = floor(√23) = 4.
α1 = 1/(√23 - 4) =
= (√23 + 4)/(23 - 16) =
= (√23 + 4)/7
a1 = floor([√23 + 4]/7) = 1
α2 = 1/[ (√23 + 4)/7 - 1] =
= 1/[(√23 + 4 - 7)/7] = 1/[(√23 -3)/7] = 7/(√23 -3) =
= 7(√23 +3)/(23 - 9) = 7(√23 +3)/14 = (√23 +3)/2
a2 = floor([√23 +3]/2 ) = 3.
α3 = 1/[(√23 +3)/2 - 3] = 1/[(√23 +3 - 6)/2 ] = 1/[(√23 - 3)/2 ] =
= 2/(√23 - 3) = 2(√23 + 3)/(23 - 9) =
= (√23 + 3)/7
a3 = floor([√23 + 3]/7) = 1.
α4 = 1/[(√23 + 3)/7 - 1] = 1/[(√23 + 3 - 7)/7 ] =
= 1/[(√23 - 4)/7 ] = 7/(√23 - 4) = 7(√23 + 4)/(23-16) =
= √23 + 4
a4 = floor(√23 + 4) = 8.
α5 = 1/(√23 + 4 - 8) = 1/(√23 - 4)
This turns out to be the same value as α1 so we are done.
√23 = [ 4, 1, 3, 1, 8 ]
We note that:
n = 1 [Position where repetition begins is a1]
p = 4 [Size of period. The representation repeats every four items]
In a previous blog, I explained how continued fractions can be used to solve Pell's Equation. In today's blog, I will go into more detail about a method for determining the representation of a continued fraction. This method is assumed in the solution to Pell's Equation which is found here.
Today's blog is based on the Jody Esmonde and M. Ram Murty's Problems in Algebraic Number Theory.
Theorem: For any irrational number α, it is possible to represent it in the form
[ a0, a1, ... ] where all values ai are integers and where we use the following equations:
(a) α0 = α
(b) ak = floor(αk)
(c) αk+1 = 1 / (αk - ak)
(1) First, I show this is true for the case k = 0.
α = α0 = floor(α0) + [α0 - floor(α0)] =
= a0 + 1/α1
(2) Assume it is true up to [a0, ..., αk]
(3) We see that:
αk = floor(αk) + [αk - floor(αk] =
= ak + 1/αk+1 =
[ a0, ..., ak, αk+1]
(4) By the Principle of Induction (see here), we are done.
QED
To show how this method can be used, let's apply it some examples:
Example 1: √6
a0 = floor(√6) = 2.
α1 = 1 / (√6 - 2) =
= (√6 + 2)/(6 - 4) =
= (√6 + 2)/2
a1 = floor([√6 + 2]/2) = 2
α2 = 1/[(√6 + 2)/2 - 2] =
= 1/[(√6 + 2 - 4)/2] =
= 1/[(√6 - 2)/2] =
= 2/(√6 - 2) =
= 2(√6 + 2)/(6 - 4) = 2(√6 + 2)/2 =
= √6 + 2
a2 = floor(√6 + 2) = 4.
α3 = 1/(√6 + 2 - 4) =
= 1/(√6 - 2) =
= (√6 + 2)/2
Since, this is the same as α1 so we have reached a repetition and we are done.
√6 = [ 2, 2, 4 ]
We note that:
n = 1 [Position where repetition begins is a1]
p = 2 [Size of period. The representation repeats every two items]
Example 2: √23
a0 = floor(√23) = 4.
α1 = 1/(√23 - 4) =
= (√23 + 4)/(23 - 16) =
= (√23 + 4)/7
a1 = floor([√23 + 4]/7) = 1
α2 = 1/[ (√23 + 4)/7 - 1] =
= 1/[(√23 + 4 - 7)/7] = 1/[(√23 -3)/7] = 7/(√23 -3) =
= 7(√23 +3)/(23 - 9) = 7(√23 +3)/14 = (√23 +3)/2
a2 = floor([√23 +3]/2 ) = 3.
α3 = 1/[(√23 +3)/2 - 3] = 1/[(√23 +3 - 6)/2 ] = 1/[(√23 - 3)/2 ] =
= 2/(√23 - 3) = 2(√23 + 3)/(23 - 9) =
= (√23 + 3)/7
a3 = floor([√23 + 3]/7) = 1.
α4 = 1/[(√23 + 3)/7 - 1] = 1/[(√23 + 3 - 7)/7 ] =
= 1/[(√23 - 4)/7 ] = 7/(√23 - 4) = 7(√23 + 4)/(23-16) =
= √23 + 4
a4 = floor(√23 + 4) = 8.
α5 = 1/(√23 + 4 - 8) = 1/(√23 - 4)
This turns out to be the same value as α1 so we are done.
√23 = [ 4, 1, 3, 1, 8 ]
We note that:
n = 1 [Position where repetition begins is a1]
p = 4 [Size of period. The representation repeats every four items]
Subscribe to:
Posts (Atom)
