Today's blog is based on H. M. Stark's An Introduction to Number Theory. If you are not familiar with Continued Fractions, start here. If you are not familiar with the Continued Fraction approximation algorithm, start here.
A continued fraction breaks a real number into a series of integers such as a0, a1, ... an. It makes sense that we can use matrices to reason about them.
In today's blog, I will focus on the simplest properties of matrices. For example, I will only deal with two types of matrices:
1 x 2 matrices such as (5,6)
2 x 2 matrices
For those who would need a review of simple matrices, matrix products, determinants, inverses, or some basic lemmas, start here.
To represent, continued fractions as matrices, we define the following:
(a) An
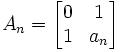
NOTE: an is taken directly from the continued fraction. See here for details on how this is generated.
(b) Mn
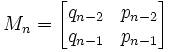
NOTE: pn, qn are generated based on the continued fraction approximation function. See here for details on how these two values are generated.
(c) γn
γn = qn-2 + αnqn-1
NOTE: αn is generated based on the continued fraction for α (see here). qn is generated based on the continued fraction approximation algorithm (see here).
Using these definitions, I will go through some lemmas that will be useful in solving Pell's equation.
Lemma 1: Mn+1 = AnMn
(1) AnMn =
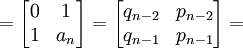
NOTE: By the definitions above.
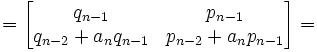
NOTE: By carrying out the matrix product [see here for review if needed]
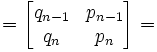
NOTE: By applying the definitions of pn and qn [see here for details]
= Mn+1 [By the definition above]
QED
Lemma 2: γn(1,α) = (1,αn)Mn
(1) (1,αn)Mn =
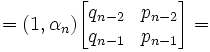
= (qn-2 + αnqn-1 , pn-2 + αnpn-1) [See here to review matrix products]
= (qn-2 + αnqn-1)(1,α) [Since α * (qn-2 + αnqn-1) = pn-2 + αnpn-1; see here]
= γn(1,α)
QED
Lemma 3: α is irrational → γn ≠ 0
(1) Since α is irrational, αn is irrational. (See here for proof; only rational numbers give way to rational αn)
(2) Assume γn = 0.
(3) Then, qn-2 + αnqn-1 = 0.
(4) Then qn-2=0 and qn-1 = 0. [See here for proof]
(5) q-1 = q1 - q0a1 = a1 - a1(1) = 0
q-2 = q0 - q-1a0 = 1 - 0*a0 = 1
NOTE: See here for review of qn
(6) We also know for all values n ≥ 1, that qn ≥ 1 (see here).
(7) So (#4) is impossible and we reject our assumption.
QED
Lemma 4: det(Mn) = (-1)n
(1) det(Mn) = pn-1qn-2 - pn-2qn-1 (See here for a review of determinants)
(2) So, det(Mn) = (-1)n by a previous result. (See here)
QED
Lemma 5: Mn+1 = AnAn-1...A1A0
(1) Mn+1 = AnMn (From Lemma 1 above)
(2) Applying Lemma 1 again gives us:
Mn+1 = AnAn-1Mn-1
(3) Since n is an integer greater than 0, we can keep on doing this until eventually we get:
Mn+1 = AnAn-1...A1A0
NOTE:
(a) p-1 = p1 - p0a1 = a0a1 + 1 - a0a1 = 1.
(b) q-1 = 0 (see Lemma 3 above)
(c)
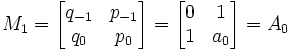
QED
Lemma 6: Mn-1 is a 2 x 2 matrix of integers.
Mn-1 =
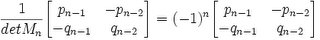
NOTE: det(Mn) = (-1)n from Lemma 4 above.
QED

3 comments:
This site is terrific. Thanks for putting in all the effort.
There are some minor typos on this page. Near the top is a line that reads:
1 x 2 matrics such as (5,6)
The word "matrics" is misspelled. Also, the first 2x2 matrix under Lemma 1 has p_n-2 in the lower right entry, when it should be p_n-1.
Hi Bob,
Thanks very much for your feedback on the site! :-)
I also appreciate you pointing out the typos. I just fixed them.
Cheers,
-Larry
In the first image of Lemma 1:
There is an equals sign between the two matrices instead of a multiplication sign.
Rob
Post a Comment