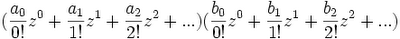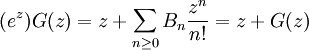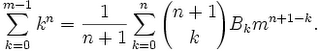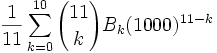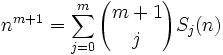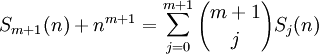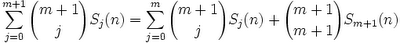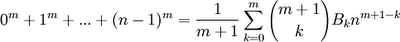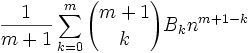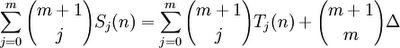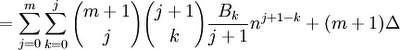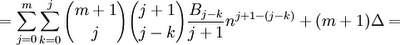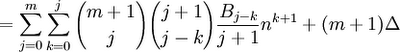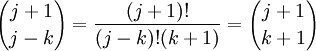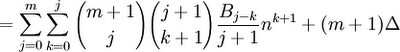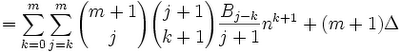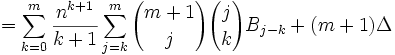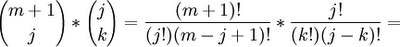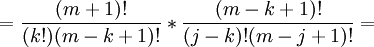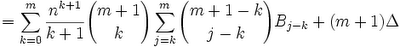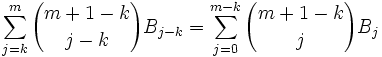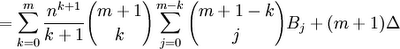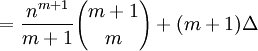Bernoulli Polynomials

In today's blog, I introduce Bernoulli polynomials and show how they can be used to present an even shorter version of the summation formula we found for Bernoulli numbers.

The content in today's blog is taken from Concrete Mathematics (Graham, Knuth, and Patashnik, 1989).

Definition 1: Bernoulli Polynomial



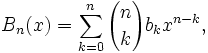
where n ≥ 0 and b_k is the Bernoulli number (see Definition 1, here)

I will now show how Bernoulli Polynomials can be used to create a concise summation formula.

Lemma 1: ∑ (k=0,n) e^kz = [e^nz - 1]/[e^z - 1]

Proof:

(1) Let S_n = ∑ (k=0,n-1) e^kz = ∑ (k=0, n) (e^z)^k = e⁰ + e^z + e^2z + ... + e^(n-1)z

(2) S_n + (e^z)ⁿ = (e^z)⁰ + ∑ (k=0,n-1) (e^z)^k+1

(3) (e^z)S_n = (e^z)∑ (k=0,n-1) (e^z)^k = ∑ (k=0,n) (e^z)^k+1

(4) Putting #2 and #3 together gives us:

S_n + (e^z)ⁿ = (e^z)S_n + 1

(5) So, solving for S_n gives us:

S_n - (e^z)S_n = 1 - (e^z)ⁿ = S_n(1 - e^z)

(6) Dividing both sides by (1 - e^z) gives us:

S_n = [1 - (e^z)ⁿ]/[1 - e^z] *(-1)/(-1) = [e^nz - 1]/[e^z - 1]

QED

NOTE: If you are not familiar with the idea of generating functions, start here.

Corollary 1.1: Generating Function for Bernoulli Polynomials

∑ (m ≥ 0) B_m(n)z^m/m! = (ze^xz)/(e^z - 1)

Proof:

(1) Let T(z,n) be the generating function for Bernoulli polynomials B_m(n) so that we have:

T(z,n) = B₀(n)z⁰/0! + B₁(n)z¹/1! + .... = ∑ (m=0,∞) B_m(n)z^m/m!

(2) Inserting the definition for Bernoulli polynomials (see Definition1 above), we have:

T(z,n) = ∑ (m=0,∞) ∑(k=0; m) [(m!/[k!][m-k]!)*B_kx^n-k] z^m/m!

(3) Using a previous result on binomial convolution (see Lemma 1, here), we can reverse this to get:
∑(m=0; ∞) ∑(k=0;m) [(m!/[k!][m-k]!)*B_kx^n-k] z^m/m! = [∑(m=0; ∞) B_mz^m/m!]*[∑(m=0, ∞) x^mz^m/m!]

(4) From a previous result (see Theorem, here), we have:

∑ (m ≥ 0) (B_m)z^m/m! = z/[e^z - 1]

(5) Further, using the power series for e (see Lemma 2, here), we have:

e^xz = ∑ (m ≥ 0) x^mzm/m!

(6) Inserting these results gives us:

T(z,n) = ∑(m=0; ∞) ∑(k=0;m) [(m!/[k!][m-k]!)*B_kx^n-k] z^m/m! = [∑(m=0; ∞) B_mz^m/m!]*[∑(m=0, ∞) x^mz^m/m!] =

= (z/[e^z - 1])*(e^xz) = (ze^xz)/(e^z - 1)

QED

Theorem: S_m-1(n) = (1/m)(B_m(n) - B_n(0))

Proof:

(1) S_m(n) = 0^m + 1^m + ... + (n-1)^m = ∑ (k=0,n) k^m [See Definition2, here for definition of S_m(n)]

(2) Let S(z) = ∑ (m ≥ 0) S_m(n) z^m = S₀(n) + S₁(n)z + S₂(n)z² + ... = ∑ (m ≥ 0) ∑ (k=0,n) k^mz^m

(3) Using the power series for e^z (see Lemma 2, here), we know that:

e^z = ∑ (n ≥ 0) zⁿ/n! = z⁰/0! + z¹/1! + ... + zⁿ/n!

(4) We can see that:

e^kz = ∑ (m ≥ 0) (kz)^m/m! = ∑(m ≥ 0)k^mz^m/m!

(5) Let G(z,n) be the generating function for S(z) so that we have:

G(z,n) = S₀(n)x⁰/0! + S₁(n)z¹/1! + S₂(n)/z²/2! + ... = ∑ (m ≥ 0) S_m(n)z^m/m!

(6) Using step #2, then we have:

G(z,n) = ∑ (m ≥ 0) ∑ (k=0, n) k^mz^m/m! = ∑ (k=0,n) e^kz

(7) Using the Lemma 1 above, we have:

G(z,n) = [e^nz - 1]/[e^z - 1]

(8) Let T(z,n) be the generating function for the Bernoulli Polynomial

(9) Using Corollary 1.1 above, we have:

T(z,n) = ∑ (m ≥ 0) B_m(n)z^m/m! = (ze^xz)/(e^z - 1)

(10) This then gives us that:

T(z,n) - T(z,0) = (ze^nz)/(e^z - 1) - (ze^0z)/(e^z - 1) = z[e^nz - 1]/[e^z-1]

(11) This shows that z*G(z,n) = [T(z,n) - T(z,0)]

(12) So that we have:

S₀(n)z¹/0! + S₁(n)z²/1! + S₂(n)/z³/2! + ... = [(B₀(n)z⁰/0! + B₁(n)z¹/1! + ....) - (B₀(0)z⁰/0! + B₁(0)z¹/1! + ....)]

(13) Lining up, equal powers of zⁱ gives us:

S_m-1(n)/(m-1)! = B_m(n)/m!] - B_m(0) /m!

(14) Multiplying both sides by (m-1)! gives us:

S_m-1(n) = (1/m)[B_m(n) - B_m(0)]

<sub>QED

References</sub>

• "Bernoulli Polynomials", Wikipedia.com
• Ronald L. Graham, Donald E. Knuth, Oren Patashnik, Concrete Mathematics, Addison-Wesley, 1989

A Generating Function for the Bernoulli Numbers

In my previous blog, I defined the Bernoulli numbers using a recurrence relation:

In today's blog, I will show how the Bernoulli numbers can be used with a generating function. A generating function is a power series, that is, a compact expression that defines an infinite sum. For background on generating functions, I recommend the wikipedia article (see reference) or Graham et al's Concrete Mathematics (see reference).

The content in today's blog is taken from Concrete Mathematics. The term "binomial convolution" is taken from this work. A "convolution" is the multiplication of two generating functions. This lemma is called a "binomial convolution" by Graham et al because the result involves binomial coefficients (see binomial theorem, here, for more details).

Lemma 1: Binomial Convolution

Let:





h(z) = f(z)*g(z)

Then there exists d_n such that:



with:



Proof:

(1) Multiplying f(z) with g(z) gives us:



(2) Grouping the result by zⁱ gives us:



(3) If we set c_i to each coefficient. For example, if we set c₀ to (a₀b₀)/(0!0!), then we have the following formula:



(4) Now, let's define a value d_i such that:



(5) This then gives us that:
d_i/(i!) = c_i


(6) Combining step #5 with step #2 and step #3 gives us:



QED

Thereom: Generating Function for the Bernoulli Numbers

z/(e^z - 1) is the generating function for the Bernoulli numbers

Proof:

(1) Let G(z) = ∑ (n ≥ 0) B_nzⁿ/n! where B_i is the Bernoulli number for i.

(2) We know from a previous result (see Lemma 2, here) that:

e^z = ∑ (n ≥ 0) zⁿ/n!

(3) So we can use Lemma 1 above to show that:



(4) Now, the definition for Bernoulli numbers (see Definition 1, here) is:



for all cases except for B₀ where B₀ = 1.

(5) If we let n=m+1 and add B_n to both sides, then we have:



or B_n + 1 in the case where n=m+1=1.

(6) This enables us to simplify the result in step #3 to get:



Note: the z at the bottom comes from the fact that at n=1, our result is (B₁+1)z¹/1! = B₁z¹/1! + z.

(7) If we subtract G(z) from both sides, we get:

(e^z)G(z) - G(z) = z =

G(z)(e^z - 1) = z

(8) Dividing both sides by e^z - 1 gives us:

G(z) = z/(e^z - 1)

QED

Corollary: B_2i+1=0 if i ≥ 1.

Proof:

(1) z/(e^z - 1) = ∑ (n ≥ 0) B_nzⁿ/n! [This follows from the theorem above]

(2) Now, B₁ = -(1/2) [See Definition 1, here]

(3) So,

z/(e^z - 1) + (z/2) = ∑ (n ≥ 0 and n ≠ 1) B_nzⁿ/n!

We subtract (-z/2) instead of -1/2 because we are removing this item from a generating function where each value in the sum z/(e^z-1) pairs up with a unique term of the sum.

In this case, B₁ matches up with the term B₁(z¹)/1! which equals -z/2.

(4) z/(e^z - 1) + (z/2) = (2z + z[e^z - 1])/(2[e^z-1]) = (2z -z + z[e^z])/(2[e^z-1]) =

= (z/2)(e^z+1)/(e^{z - 1})

(5) (z/2)(e^z + 1)/(e^z-1) = [e^-(z/2)/e^-(z/2)]* (z/2)(e^z + 1)/(e^z-1) =

= (z/2)[(e^z/2 + e^-z/2)/(e^z/2 - e^-z/2)]

(6) So, we see in step #5, that if we replace z with (-z), the identity remains unchanged.

(-z/2)[(e^-z/2 + e^-(-z/2)]/(e^-z/2 - e^-(-z)/2) =

= -z/2[e^-z/2 + e^z/2]/(e^-z/2 - e^z/2) =

= z/2[e^z/2 + e-z/2]/(e^z/2 - e^-z/2)

In the language of mathematics, a function is called even if f(-x)=f(x) and we call a function odd if f(-x) = -f(x). [See here for more details]

Example: cos(x) is an even function while sin(x) is an odd function. [See here for review of sin and cos]

(7) But this means that the same must hold true for ∑ (n ≥ 0 and n ≠ 1) B_nzⁿ/n!

Since by Step #3, we showed that they are equal functions.

So that we have:

∑ (n ≥ 0 and n ≠ 1) B_nzⁿ/n! = ∑ (n ≥ 0 and n ≠ 1) B_n(-z)ⁿ/n! = ∑ (n ≥ 0 and n ≠ 1) (-1)ⁿ(B_nzⁿ/n!)

(8) Matching up each of the terms according to powers of zⁿ, this gives us that:

B_n = (-1)ⁿB_n

(9) But this can only be true if B_n = 0 when n is odd.

QED

References

• "Generating Function," Wikipedia.com
• Ronald L. Graham, Donald E. Knuth, Oren Patashnik, Concrete Mathematics, Addison-Wesley, 1989
• "Odd Bernoulli Numbers are 0", PlanetMath.org
• "Even and Odd Functions", Wikipedia.com
  

Bernoulli Numbers

The Bernoulli numbers were first identified by Jakob Bernoulli in Ars Conjectandi, a work that was published after his death. The Bernoulli numbers turn up again and again in the history of mathematics. In today's blog, I will focus on the original problem that Jakob Bernoulli was attempting to solve. In a future blog, I will show how they were used by Ernst Kummer as a criteria for determining if a prime is regular.

Interestingly, Bernoulli numbers may have been discovered earlier by Seki Kowa and were rediscovered independently by a 17-year-old Srinivasa Ramanujan.

Bernoulli was analyzing formulas for the sums of powers, that have the following form:

S_m(n) = ∑ (i=1, n) i^m

He looked at, for example:

S₀(n) = n

S₁(n) = (1/2)n² - (1/2)n

S₂(n) = (1/3)n³ - (1/2)n² + (1/6)n

S₃(n) = (1/4)n⁴ - (1/2)n³ + (1/4)n²

S₄(n) = (1/5)n⁵ - (1/2)n⁴ + (1/3)n³ - (1/30)n

S₅(n) = (1/6)n⁶ - (1/2)n⁵ + (5/12)n⁴ - (1/12)n²

S₆(n) = (1/7)n⁷ - (1/2)n⁶ + (1/2)n⁵ - (1/6)n³ + (1/42)n.

S₇(n) = (1/8)n⁸ - (1/2)n⁷ + (7/12)n⁶ - (7/24)n⁴ + (1/2)n²

S₈(n) = (1/9)n⁹ - (1/2)n⁸ + (2/3)n⁷ - (7/15)n⁵ + (2/9)n³ - (1/30)n

S₉(n) = (1/10)n¹⁰ - (1/2)n⁹ + (3/4)n⁸ - (7/10)n⁶ + (1/2)n⁴ - (3/20)n²

S₁₀(n) = (1/11)n¹¹ - (1/2)n¹⁰ + (5/6)n⁹ - n⁷ + n⁵ - (1/2)n³ + (5/66)n.

By looking at these formulas, he noticed a pattern and in analyzing this pattern, he came up with what were termed Bernoulli numbers by Abraham de Moivre.

Well, for each S_m(n), we can see that:

1) the first term is 1/(m+1)*n^m+1

2) the second term, when it exists, is (-1/2)n^m

3) the third term, when it exists, is (m/12)*n^m-1

4) the fourth term, when it exists, is (-m)(m-1)(m-2)/720*n^m-3

Bernoulli had discovered that if he defined a sequence of the numbers, he got a simple formula for defining the sum of powers.

The formula he discovered was the following:



In the above formula, B_k refers to the sequence of Bernoulli numbers where Bernoulli numbers are defined in the following way:

Definition 1: Bernoulli Numbers



with B₀ = 1.

As a convention, I will refer to Bernoulli numbers as B_i.

So, to figure out, B₁, we have:



This gives us:

2*B₀ + 2*B₁ = 0

B₁ = (1/2)[-2*B₀] = (-1/2)(1) = (-1/2)

We determine B₂ based on solving:



In this way, we find that:

B₀ = 1
B₁ = -(1/2)
B₂ = (1/6)
B₃ = 0
B₄ = -(1/30)
B₅ = 0
B₆ = (1/42)
B₇ = 0
B₈ = -(1/30)
B₉ = 0
B₁₀ = (5/66)
B₁₁ = 0
B₁₂ = -(691/2730)

Bernoulli wrote that he was able to use his formula to compute S₁₀(1000) in less than 10 minutes (see Smith, A Source Book in Mathematics, below).

Using his formula, this comes down to:





Evaluating this gives us:

91,409,924,241,424,243,424,241,924,242,500

I will now show a proof for Bernoulli's formula for sums. This is taken straight from Graham et al. Concrete Mathematics.

Definition 2: S_m(n)

Let S_m(n) = 0^m + 1^m + ... + (n-1)^m

I will use this shorthand in the lemma and theorem below.

Postulate 1: 0⁰ = 1

(This is taken from Graham et al.)

Graham et al argue in Concrete Mathematics that if we let 0⁰ = 1, it provides a more elegant notation for the Binomial Theorem. Their argument is that the Binomial Theorem is very important while 0⁰ is almost irrelevant. (see Concrete Mathematics, page 162).

Lemma 1:



Proof:

(1) S_m+1(n) + n^m+1 =

= ∑(k=0,n-1) k^m+1 + n^m+1 =

= ∑(k=0,n) k^m+1 =

= 0^m+1 + ∑(k=1,n) k^m+1 = ∑(k=1,n) k^m+1 =

= ∑ (k=0,n-1) (k+1)^m+1

(2) Using the Binomial Theorem, we get:



(3) Putting this together with step #1 gives us:



This gives us:



(4) Since S_j(n) = o^j + 1^j + ... + (n-1)^j, we have shown that:



(5) Now, since



The conclusion follows from simple subtraction since [(m+1)!]/[(m+1)!(0)!] = 1.

QED

Theorem:



Proof:

(1) We can see that this is true for m=0 since:

S₀ = n = (1/[1+1])∑ (k=0,0) ([0+1]!/k![1-k]!)B_kn^0+1-k =

= (1)*(1!/[0!][1!])B₀n¹ = (1)*(1)*(1)*n = n [Since B₀ = 1, see above]

(2) Let's assume that this is true up to m-1.

(3) Let T_m(n) =



(4) Let Δ = S_m(n) - T_m(n)

(5) Using Lemma 1 above, we know that:



(6) Using our definition of Δ, we can also see that:



(7) The goal in this proof will be to show that Δ = 0.

(8) Adding the definition of T_j(n) [see step#3] gives us:



I also simplified [(m+1)!/(m!)(1!)] to (m+1).

(9) We can move all values that are independent of k before the ∑ (k=0,j):



(10) Since we can change the order of the terms of a finite sum and still get the same result, we can switch each value of k with (j-k) to get:






(11) Now, since (j+1) - (j-k) = k+1, we have:



(12) Putting this result in step #11 gives us:



(13) We can see that in step #12, 0 ≤ k ≤ j ≤ m. The sum is in fact all combinations of j,k where this is the case. This means that we can rearrange the sum to the following:



(14) Since n^k+1 is independent of j, we can move it over to get the following:



(15) Since,



we can also rearrange the result in step #14 to give us:



(16) Since:











We can rearrange terms to get:



(17) Since:



We can rearrange terms to get:



(18) Now, we know from the definition of Bernoulli numbers (see Definition 1 above) that



in all cases except where m = 0. This occurs only when k = m.

This allows us to simplify the result in step #17 to the following:



(19) Now since [(m+1)!/(m!)(1!)] = m+1, we get:

= n^m+1 + (m+1)Δ

(20) But in step #5, we started out with n^m+1 so we are left with:

n^m+1 = n^m+1 + (m+1)Δ.

(21) The only way that this is true is if Δ = 0.

QED

In another blog, I show how z/[e^z - 1] can be used as a generating function for the Bernoulli numbers.

References

• Ronald L. Graham, Donald E. Knuth, Oren Patashnik, Concrete Mathematics, Addison-Wesley, 1989
• David Eugene Smith, A Source Book in Mathematics, Dover, 1959
• "Bernoulli Numbers", Wikipedia.Com
  

Johann Bernoulli

Johann Bernoulli was born July 27, 1667 in Basel Switzerland. He was the tenth born child of a wealthy, prominent Swiss family. His father tried to interest him in the thriving family spice business but it did not work out. When Johann was 15, he began working for his father's company but this only lasted a year.

Johann started at the University of Basel in 1683. His father encouraged him to study medicine. His older brother Jacob had already begun to make a name for himself in mathematics and physics. Johann soon took an interest to math and studied under his brother's guidance. For two years, the brothers studied the new methods of Gottfriend von Leibniz which had recently been published. Johann showed a tremendous ability for the new mathematics and after these two years, in many ways became the mathematical equal of his more experienced, older brother.

In 1690, Johann published his first scientific paper on the process of fermentation. Later, in 1691, he went to Geneva to lecture on the new differential calculus. He traveled to France, like his brother had, and met with the followers of Rene Descartes who were led by Nicolas Malebranche. In France, Johann met Gillaume Francois Antoine Marquis de L'Hopital who was considered one of the finest of the Paris mathematicians. Johann taught L'Hopital about the calculus and Leibniz's methods. L'Hopital paid Johann well for the lessons and Johann continued the lessons via correspondence after he returned to the University of Basel.

Even while Johann studied medicine, he was continually publishing mathematical papers. He even began a very substantial correspondence with Leibniz on the ideas of calculus. In 1694, when Johann submitted his paper on medicine, the content of the paper was the mathematics of muscular movement.

He continued to generate significant mathematical papers and in 1695, he was offered the chair of mathematics at Groningen. This was offered based on the recommendation of Christiaan Huygens. Johann was glad to accept even though the move to Groningen was difficult.

While in Groningen, he got involved in many controversies. One of his medical lectures was criticized as casting doubt on the possibility of ressurection. One of his students accused him of abandoning Calvinism in order to embrace the philosophy of Descartes. Johann and his brother Jacob also began a fierce rivalry as each brother tried to outdo the other.

L'Hopital would later publish the first book on calculus. This book contained the famous L'Hopital's Rule which may have come from Johann Bernoulli.

Johann became a bit bothered by L'Hopital's book because he did not feel that it paid him proper acknowledgment. L'Hopital wrote in the book (quoted on the MacTutor web site):

And then I am obliged to the gentlemen Bernoulli for their many bright ideas; particularly to the younger Mr Bernoulli who is now a professor in Groningen.

When L'Hopital died in 1704, Johann insisted that most of the content of the book had been taken from him. At the time, few believed him. In 1922 (according to the MacTutor web site), evidence surfaced which substantiated Johann's claims which included mathematical proofs that were virtually identical to the proofs included L'Hopital's book.

Johann had married shortly before moving to Gottigen and in 1705, he learned that his father-in-law was very sick and not expected to live much longer. Johann and his family moved back to Basel. Once there, he learned that his father-in-law had made a recovery but his brother Jacob had died of tuberculosis. Johann decided to stay in Basel and took over after his brother as the Chair of Mathematics at the University of Basel.

In 1713 when Leibniz and Sir Isaac Newton quarrelled about who came first with regard to calculus. Johann weighed in on the size of Leibniz. Johann argued that Leibniz's methods were more powerful than Newton's (a position that is generally supported today) and that Descarte's theory of vortex was superior to Newton's theory of gravitation. This controversy has been documented in a new book that came out this year.

Three of Johann's sons would go on to become famous mathematicians. In 1734, his son Daniel published what would become one of his most important books. Johann proceeded to publish his own version of the same topic and claimed to have finished it in 1732. It is interesting that such a giant in mathematics would feel the need to compete with his own son.

Johann died on January 1, 1748 in Basel, Switzerland. At this time, his fame was giant. His contributions had been recognized by the scientific academies of Paris, Berlin, London, St. Petersburg, and Bologna.

References

• Biography of Johann Bernoulli, MacTutor
  

Jacob Bernoulli

Jacob Bernoulli was the oldest of the famous Bernoulli mathematicians. His younger brother Johann and his nephew Daniel all went on to become very famous and important mathematicians.

Jacob was born on December 27, 1654 to a prominent and wealthy family of merchants in Basel, Switzerland. His grandfather had started a prosperous spice business in Amsterdam but then had immigrated to Switzerland when Spain began a crackdown on protestants in 1567.

Jacob's father, Nicholas, was a member of the town council and a magistrate. His mother was the daughter of an important Basel banker. When the time came for Jacob to enter the university, he was strongly encouraged by his parents to study philosphy and theology. This apparently was the pathway to becoming a minister. He graduated from the University of Basel in 1676 with a licentiate in theology and a master's degree in philosophy. This same year, he moved to Geneva where he worked as a tutor.

All throughout his coursework, Jacob had also been studying astronomy and mathematics. Despite his parents discouragement of these pursuits, Jacob later traveled to France to study with the followers of Descartes who were led by Nicholas Malenbranche. In 1681, Jacob traveled to the Netherlands where he met with numerous mathematicians including Johanne Hudde. After this, he traveled to England where he met with Robert Boyle, Robert Hooke, and many others. In these travels, Bernoulli made numerous contacts and developed an extensive correspondence with many of the most influential mathematicians and scientists of his day. He would be offered a position with the church in Switzerland, to the great joy of his parents, but he turned it down.

He returned to the University of Basel in 1683 to teach courses in mathematics and theoretical physics. Bernoulli became fascinated with infinitesimal geometry as well as the works of Franz van Schooten, John Wallis, Isaac Barrow, and of course, the Geometrie by Rene Descartes. Jacob published many of his ideas in the math journal Acta Eruditorium which was founded in Leipzig in 1682.

Around this time, Jacob married Judith Stupanis and had two children. Neither of whom became interested in mathematics or physics. This is interesting considering the large number of Bernoullis who would become famous scientists. The New Dictionary of Scientific Biography, for example, lists 13 Bernoullis in its biographies.

Jacob's younger brother Johann was encouraged by the family to study medicine. While pursuing a medical degree, Johann was taught mathematics by Jacob. Both brothers became especially interested in Gottfried Wilhelm von Leibniz's paper on differential calculus which had just been published in Acta Eruditorum in 1684. At that time, Leibniz's paper had not yet made the impact that it would later make so the Bernoulli's interest in it represented a deeper understanding of the ideas involved. As Johann's mathematical abilities began to shine bright, there arose a falling out between the two brothers which would later become an out-and-out rivalry. The MacTutor Biography of Jacob Bernoulli says:

"...both made contributions to mathematics of the very greatest importance. Whether the rivalry spurred them on to greater things or whether they might have achieved more had they continued their initial collaboration, it is impossible to say."

Jacob Bernoulli went on to make a very significant mark on the mathematical world. He wrote on a wide range of topics including the parallels between logic and algebra, probability, infinite series, geometry, and calculus. In his geometry, he offered a method for dividing a triangle into four equals parts with two parallel lines; in probability, he offered a mathematical interpretation of relative frequency; on infinite series, he wrote about ∑ 1/n² which later became known as the Basel Problem (and would later be solved by Leonhard Euler) and wrote about exponential series that would later lead Euler to his creation of the constant e. In calculus, he wrote about the isochrone (a curve of constant descent that had been studied by Christiaan Huygens and Lebiniz) and showed how its path can be characterized by a first order nonlinear differential equation (this paper is also historically the first time that the term "integral" is used in the modern sense).

Jacob's other contributions include his analysis of what is today known as the Bernoulli equation: y'= p(x)y + q(x)yⁿ, a general method for determining the evolutes of a curve, did important work with parabolas, logarithmic spirals, epicycloids, what is today known as the lemniscate of Bernoulli, and the Drawbridge Problem (a problem regarding the keeping of a weight and draw bridge balanced).

Jacob Bernoulli became the chair of mathematics and the University of Basel and held this post until his death in 1705. Eight years after his death, his greatest work Ars Conjectandi was published. It was unfinished but would have a great impact on the theory of probability and introduced the idea of what would later be called Bernoulli Numbers.

The Dictionary of Scientific Biography (as quoted from the MacTutor web site) wrote this about Jacob Bernoulli's contribution:

Bernoulli greatly advanced algebra, the infinitesimal calculus, the calculus of variations, mechanics, the theory of series, and the theory of probability. He was self-willed, obstinate, aggressive, vindictive, beset by feelings of inferiority, and yet firmly convinced of his own abilities. With these characteristics, he necessarily had to collide with his similarly disposed brother. He nevertheless exerted the most lasting influence on the latter.

Bernoulli was one of the most significant promoters of the formal methods of higher analysis. Astuteness and elegance are seldom found in his method of presentation and expression, but there is a maximum of integrity.

After his death, his brother Johann became the chair of mathematics at the University of Basel.

References

• Biography of Jacob Bernoulli, MacTutor Web Site