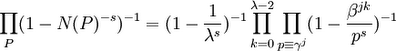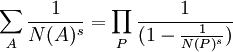Lodovico Ferrari

Lodovico Ferrari was born on February 2, 1522. His father died when he was very young so he lived with his uncle Vincent Ferrari. The mathematician Gerolamo Cardano was looking for a servant. Vincent's son Luke took the job but decided he didn't like it and left. Cardano then brought the matter up with Vincent. Vincent sent Lodovico to Cardarno in Luke's place.

On November 30, 1536, fourteen-year old Ferrari became Cardano's servant. Over time, Cardano was very impressed by Ferrari's intelligence and soon began to teach him mathematics. Ferrari began to collaborate with Cardano on his manuscripts and by the time that Ferrari was 18, he began to lecture on mathematics.

In 1540, Ferrari came up with the general solution for the quartic equation. Cardano would later publish this method in his famous book Ars Magna. In 1541, when Cardano resigned his post in mathematics in Milan, Ferrari, then 20, was able to succeed him.

Cardano had earlier solved the general cubic equation which extended a method he had learned from Nicolo Tartaglia. Cardano had promised Tartaglia that he would not publish the method until after Tartaglia published. It was this agreement that held up the publishing of Ars Magna. Cardano was very anxious to publish the work and when he found that Tartaglia's method was based on the method of Scipione del Ferro, he decided in 1545 to publish the work despite his promise to Tartaglia.

Ferrari supported Cardano in the resulting controversy and challenged Tartaglia to a public debate. Ferrari was not yet a well known mathematician so Tartaglia refused to debate him and insisted on challenging Cardano. Nothing happened for three years. Then, in 1548, Tartaglia was offered an important position in mathematics on the condition that he publicly debated Ferrari. By this time, the controversy between the two had become very public and there was a strong popular interest in this mathematical challenge.

The open debate occurred on August 10, 1548 in Milan. It occurred in front of a large crowd. By this time, Ferrari had mastered both the cubic and quartic equations. In the course of the discussion, it was clear that Ferrari was the master of the two and before the contest ended, Tartaglia decided to withdraw. In this way, Ferrari's reputation was greatly established as one of Italy's top mathematicians.

From this point on, Ferrari accepted a series of well paid positions and in 1565, he moved to Bologna where he stayed with his recently widowed half-sister and worked as a professor to the University of Bologna. Within one year, he died very suddenly. It was rumored that he had been poisoned by his half sister who sought to inherit his great wealth. Indeed, after his death, she received all of his estate. Then, she remarried and her husband absconded with all her money.

References

• "Lodovico Ferrari", MacTutor Biography
• "Tartaglia-Cardano Dispute", MacTutor Biography
  

Girolamo Cardano

Girolamo Cardano's father Fazio Cardano, a lawyer by profession, had a deep interest in mathematics. He had developed a reputation as an expert and lectured on geometry at the University of Pavia. It was said that Leonardo da Vinci once consulted with him on mathematics.

Chiara Cardano, Girolamo's mother, was a widow with three children when Fazio met her. This was a time of the plague and when Chiara was close to giving birth, she traveled to Pavia to avoid the plague which had hit Milan where she lived. She would later learn that her three children had caught the plague and died. When Cardano was born, his parents were not married.

Cardano was born on September 24, 1501. He was a sickly child. As he grew older, he worked as an assistant to his father where he learned mathematics. Despite his interest in mathematics, when he entered the University of Pavia, he decided to study medicine.

This was a time of instability and war in Italy and when the University of Pavia was temporarily shut down, Cardano transferred to the University of Padua.

It was at this same time that his father died. Cardano received a small inheritance which he quickly spent. He began to rely on gambling as a source of income.

In 1525, Cardano graduated from the university and sought to become a member of Milan's College of Physicians. His application was rejected because of his illegitimate birth.

Cardano tried to set up a medical practice in a small town. There, he met his wife, Lucia but was unable to succeed as a physician. He applied again to the College of Physicians in Milan and again was rejected. By 1533, gambling was taking up his time and money. He pawned his wife's jewelry at this time and found himself in the poorhouse.

Cardano's fortune changed when he managed to get his father's old position as lecturer in mathematics. At the same time, his medical practice began to take off even though he had not been accepted by the College of Physicians. In 1536, he wrote a book critical of the College of Physicians. Despite this, his reputation and influence grew. Using his growing social connections, he was able to become a member of College of Physicians in 1538.

In 1539, he heard about the mathematician Tartaglia who had discovered a method to solve certain forms of cubic equations. He convinced Tartaglia to reveal the details of his method which Tartaglia did on the condition that Cardano wouldn't publish the method unless Tartaglia published it first.

Over the next six years, Cardano began to study cubic and quartic equations. It was at this time that he was able to come up with a general solution for the cubic equations using radicals. This was a significant advance over the method of Tartaglia.

Later, Cardano's assistant, Lodovico Ferrari came up with a general solution of quartic equations using radicals. In 1545, Cardano published his very important book Ars Magna in which he discussed the general solution for the cubic equation and the quartic equation. The book was a best seller and established Cardano's reputation as a great mathematician. There is much that has been written about the dispute between Cardano and Tartaglia so I will not write about it here. (See the references for more details.)

In 1546, his wife Lucia died. By this time, he had become rector of the College of Physicians in Milan. He once traveled to Scotland in order to provide a cure for Archbishop of St. Andrews. The archbishop made a complete recovery. Cardano was now helping a very rich set of clients. He was a wealthy man and he became professor of medicine at Pavia University.

Cardano's eldest son was in an unhappy marriage. After years of unhappiness, he poisoned his wife and confessed to the murder. The judge ruled that his son's life could be spared if Cardano could settle with the wife's parents. Such a settlement did not occur and Cardano's son was executed on April 13, 1560.

Cardano now moved to Bologna where he became a professor of medicine. His other son had a terrible gambling problem and once, when in need of money, took large amounts of money from his father. The son was later banished from Bologna for the crime.

In 1570, Cardano was accused of being a heretic for providing a horoscope and for writing a book that praised the emperor Nero. It is believed that his son helped to raise the charges. Cardano was now imprisoned for several months. On his release, he traveled to Rome where he met with the Pope. Somehow, despite everything that had occurred, the pope granted him a pension.

Cardano predicted the date of his death and sure enough, he died on that day. It is said that he committed suicide. Although, he later made peace with his son, in his will, he left all of his belongings to his grandson.

References

• "Girolamo Cardano", MacTutor Biography
  

Abu Ja'far Muhammad ibn Musa Al-Khwarizmi

Unfortunately, there are many details missing from our knowledge about Abu Ja'far Muhammad ibn Musa Al-Khwarizmi. He was born around 780 AD. It is unclear where he was born. His name Al-Khwarizmi may imply that he was from Khwarizm (Khiva) in Central Asia. Again, this may imply that his family is from Khwarizm but he himself was from Baghdad.

We do know that Al-Kwarizmi became a scholar at the House of Wisdom in Baghdad. His role was to translate books from Greek as well as write original works on mathematics, astronomy, and other topics. The House of Wisdom was an academy that had been set up by Al-Mamun who became caliph of the Arab Empire in 813 AD after defeating his brother. In addition to the House of Wisdom, Al-Mamun set up a great library and and several astronomy observatories. The library at this time was perhaps the most important collection of Greek and Byzantine books since the great library of Alexandria.

We know that Al-Khwarizmi dedicated two of his books to Caliph Al-Mamun. One of these books was on astronomy and the other book was the very famous text on algebra called Hisab al-jabr w'al-muqabala. It is from this book that we get the English work algebra (the Latin translation of the book was Liber algebrae et almucabala). This second book launched the rise of algebra in its ascendency over the geometry of the Greeks. Another of his books on arithmetic popularized what became known as Arabic numerals.

The long title of the book on algebra refers to two important operations. al-jabr ("completion") and al-muqabala ("balancing"). The book systematizes linear and quadratic equations and focuses on numbers (as opposed to geometric shapes) which include units (a number), roots (x), and squares (x²).

The book is written almost completely in words. Even numbers are written as words. Although Al-Khwarizmi popularized the Arabic numerals in another of his books, he does not use them here. He categorizes quadratic equations into six types:

• "squares" equal "roots" (ax² = bx)
• "squares" equal number (ax² = c)
• "roots" equal number (bx = c)
• "squares" and "root" equal number (ax² + bx = c)
• "squares" and number equal "roots" (ax² + c = bx)
• "roots" and number equal "square" (bx + c = ax²)

He then presents algebraic and geometric methods for solving each of these types.

Interestingly, his book does not include a the general solution for quadratic equations even though, it is implied in the solution for each of the problems in the book. This would be first published in 1145 by Abraham bar Hiyya Ha-Nasi.

Al-Khwarizmi's book on arithmetic was called Al-Khwarizmi on the Hindu Art of Reckoning. Unfortunately, all Arabic versions of this book have been lost. The only extent book is a Latin translation.

This book on arithmetic has given us the modern word "algorithm" and it is the place where the Hindu numerals are introduced to the West and the place where 0 is used as a number. This book consists of a systematization of the Indian numerals.

Al-Khwarizmi wrote many other books including books on astronomy, geography, calendars, sun dials, and many other topics. Unfortunately, it is very difficult to know how much of this content was original and how much was taken from other sources.

What is undeniable is the great importance of Al-Khwarizmi's work and the impact it had on the rise of algebra.

One scholar has written (see the MacTutor reference):

In the foremost rank of mathematicians of all time stands Al-Khwarizmi. He composed the oldest works on arithmetic and algebra. They were the principal source of mathematical knowledge for centuries to come in the East and the West. The work on arithmetic first introduced the Hindu numbers to Europe, as the very name algorism signifies; and the work on algebra ... gave the name to this important branch of mathematics in the European world...

References

• "Muhammad ibn Musa al-Khwarizmi",Wikipedia
• "Quadratic, cubic, and quartic equations",MacTutor
• "Abu Ja'far Muhammad ibn Musa Al-Khwarizmi",MacTutor
  

Detour through Group Theory

To move ahead on the Kummer Class Formula, it is necessary to delve into Dirichlet Characters and L-Functions. Properly appreciating these ideas requires a solid understanding of cyclic groups.

I think that it makes sense at this point to take a break from Kummer's Class Formula and trace the development of group theory from the quadratic equation to Galois's famous proof.

Once I have gone into more detail about group theory and in particular, cyclic groups, I will resume the development of Kummer's Class Formula.

Derivation of the Kummer Class Formula: Step One

In the next series of blogs, I will show how the Kummer Class Formula is derived from the zeta function for cyclotomic integers. In a previous blog, I showed Kummer's proof that Fermat's Last Theorem was true for regular primes. The class formula is the method for determining whether a given prime is regular or not.

The content in today's blog is taken from Harold M. Edwards Fermat's Last Theorem: A Genetic Introduction

Lemma 1:

If β is an fth root of unity and n=ef, then:

(x - yβ)*...*(x - yβⁿ) = (x^f - y^f)^e

Proof:

(1) X^f - 1 has f distinct roots by the Fundamental Theorem of Algebra (see here)

(2) This means that:

X^f - 1 = (X - 1)(X - β)(X - β²)*...*(X - β^f-1)

(3) Since β^f = 1, we have:

X^f - 1 = (X - β)(X - β²)*...*(X - β^f-1)(X - β^f)

(4) Let X = x/y, then we have:

(x/y)^f - 1 = ([x/y] - β)([x/y] - β²)*...*([x/y] - β^f)

(5) If we multiply both sides by y^f, we get:

x^f - y^f = (x - βy)(x - β²y)*...*(x - β^fy)

(6) Further, if we put both sides to the power of e, we get:

(x^f - y^f)^e = [(x - βy)(x - β²y)*...*(x - β^fy)]^e =

= (x - βy)(x - β²y)*...*(x - β^fy)*
(x - β^f+1y)(x - β^f+2)*...*(x - β^2fy)*
...
(x - β^f(e-1)+1)(x - β^f(e-1)+2)*...*(x - β^efy) =

= (x - βy)*x - β²y)*...*(βⁿy)

QED

Theorem 2:



Proof:

(1) Since N(P)=p^f and N(α - 1)=λ (see here for p^f and here for N(α-1)=λ) and since there are e prime divisors P that divide a prime p (see here), we have:



(2) For each p, we can see that:

(1 - p^-fs)^-e = (1^f - (p^-s)^f)^-e

(3) Let γ be a primitive root mod λ

(4) For each p, let γ^j ≡ p (mod λ)

(5) Let β^j be an fth root of unity such that (β^j)^f = 1 but for any integer i less than f, (β^j)^f ≠ 1.

(6) Using Lemma 1 above, we have:

(1^f - (p^-s)^f)^e = (1 - β^jp^-s)*...*(1 - p^-sβ^jn) = ∏ (k=1, λ-1) (1 - β^jkp^-s) =

=∏ (k=0, λ-2) (1 - β^jkp^-s)

(7) Using step #6, we have:

(1 - λ^-s)^-1 ∏ (p ≠ λ) (1 - p^-fs)^-e = (1 - λ^-s)^-1 ∏ (p ≠ λ) ∏ (k=0, λ-2) (1 - p^-sβ^jk)^-1

(8) From this step, the conclusion follows:



QED

References

• Harold M. Edwards, Fermat's Last Theorem: A Genetic Introduction, Springer, 2000

The Zeta Function for Cyclotomic Integers

To get to the Kummer class formula, it is necessary to establish a zeta function for cyclotomic integers:



where A ranges over the set of ideal numbers, P ranges over the set of prime divisors of ideal numbers, and N(X) is the norm for these ideal numbers [for review of ideal numbers, start here] and s is greater than 1.

The content in today's blog is taken from Harold M. Edwards' Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory.

Theorem 1: For s greater than 1, ∏ (1 - N(P)^-s)^-1 converges absolutely

Proof:

(1) Let λ be a prime number such that α^λ = 1 for any positive integer i less than λ, αⁱ ≠ 1. [See here for review of cyclotomic integers and λ]

(2) N(P) = p^f where p is a prime divisible by the prime divisor P and f is the exponent of p mod λ (or f=1 if p = λ) [See Lemma 1, here for proof N(P)=p^f or here for f=1 if p=λ]

(3) N(P)^-s = p^-fs ≤ p^-s

(4) Let e = (λ - 1)/f [See Lemma 1, here for proof that f divides λ-1] so that e ≤ λ - 1.

(5) We know from a previous result (see Lemma 1, here), that there are e prime divisors for a given prime p so that we know that:

∑ N(P) for a given P ≤ (λ - 1)∑ p^f

(6) So that:

∑ N(P)^-s ≤ (λ - 1) ∑ p^-fs which is less than (λ - 1)∑ p^-s which is less than (λ - 1)∑ n^-s

(7) From a previous result (see Theorem 1, here), we know that ∑ n^-s converges if s is greater than 1 so, we can conclude that ∑ N(P)^-s necessarily converges.

(8) Since N(P)=p^f is greater than 0, it follows that ∑ N(P)^-s = ∑ abs(N(P)^-s) and using Lemma 3, here, we can conclude that:

∏ (1 - abs(N(P)^-s)) converges

(9) This gives us (see Definition 1, here) that ∏ (1 - N(P)^-s) converges absolutely.

(10) Using the Reciprocal Law (see Lemma 6, here), we conclude that ∏ (1 - N(P)^-s)^-1 also converges absolutely.

QED

Lemma 2: For s greater than 1, ∑ N(A)^-s ≤ ∏ (1 - N(P)^-s)^-1

Proof:

(1) Let A* be any set of A and S* be defined such that S* = ∑ (A ∈ A*) N(A)^-s

(2) Let P* be the set of prime divisors that make up any of the A in A*. [See here for a review of prime divisors of an ideal number]

(3) For each P ∈ P*, we see that (1 - N(P)^-s)^-1 = 1 + N(P)^-s + N(P²)^-s + N(P³)^-s + .... [ See Lemma 1, here]

(4) It is then clear that ∏ (1 - N(P)^-s)^-1 = the product of all of these geometric series which includes all A in A*.

(5) Since N(Pⁱ) ^-s continues ad infinitum, there also necessarily exists N(Pⁱ)^-s that is not a divisor of any N(A) where A ∈ A* since A* is a finite set by assumption.

(6) So, any partial sum is less than the partial product.

(7) In this way, we can conclude that the infinite sum ∑ N(A) ≤ the infinite product ∏ (1 - N(P)^-s)^-1

QED

Corollary 2.1: ∑ N(A)^-s converges absolutely.

Proof:

(1) By Lemma 2 above, ∑ N(A)^-s ≤ ∏ (1 - N(P)^-s)^-1.

(2) Since ∏ (1 - N(P)^-s)^-1 converges (see Theorem 1 above), then ∑ N(A)^-s necessarily converges too.

(3) Since all values N(A)^-s are positive, it follows that ∑ N(A)^-s converges absolutely. (see Definition 2, here)

QED

Theorem 3: ∑ N(A)^-s = ∏ (1 - N(P)^-s)^-1

Proof:

(1) By Lemma 2 above, we have:

∑ N(A)^-s ≤ ∏ (1 - N(P)^-s)^-1

(2) Let P* be the same set of prime divisors from Lemma 2 above.

(3) It is clear that ∏ (1 - N(P)^-s)^-1 includes as a sum a distinct set of ideal numbers but it does not include all ideal numbers since P* is a finite of P and there are an infinite number of primes p [See Theorem, here].

(4) Let A* be all the set of ideal numbers in the sum ∏ (1 - N(P)^-s)^-1 plus an ideal number A+ that is divisible by a prime divisor P that is not found in P*.

(5) It is clear that ∑ (A ∈ A*) N(A)^-s) ≥ ∏ (P ∈ P*) (1 - N(P)^-s)^-1

(6) Combining step #5 with step #1 gives us that:

∑ N(A)^-s = ∏ (1 - N(P)^-s)^-1

QED

References

• Harold M. Edwards, Fermat's Last Theorem: A Genetic Introduction, Springer, 2000.

lim (s ↓ 1) (s-1)ζ(s) = 1

Before beginning the derivation of Kummer's class formula for cyclotomic integers, it is necessary to review one important property from the Riemann zeta function.

The content in today's blog is taken from Harold M. Edwards' Fermat's Last Theorem.

Theorem 1: lim(s ↓ 1) (s-1)ζ(s) = 1

Proof:

(1) From a previous result (see Theorem 4, here), we know that:

ζ(s) = ∑ (1/n^s) = ∏ (1 - p^-s)^-1

and that:

for s greater than 1, both sides of this equation are absolutely convergent (see Theorem 1 and Theorem 2, here).

(2) Using the Integral Test (see Theorem 1, here),

We know that if ∑ (1/n^s) converges, then ∫ (1,∞) 1/x^sdx also converges.

(3) If we define a function so that f(x) = 1/ceiling(x)^s, we can conclude that ∫ (1,∞) 1/x^s is less than ∫ (1,∞) 1/ceiling(x)^s = ∑ (n=1,∞) 1/n^s which is less than 1 + ∫ (1,∞) 1/x^sdx since:

(a) ∫ (1,∞) 1/x^s is less than ∫ (1,∞) 1/ceiling(x)^s

At each point x ≤ ceiling(x) so that at each point x^s ≤ ceiling(x)^s.



(b) ∫ (1,∞) 1/ceiling(x)^s = ∑ (n=1,∞) 1/n^s

This follows from the fact that for each interval, ∫ (x,x+1) 1/ceiling(x)^s= ∑(n=x,x) 1/n^s.

(c) ∑ (n=1,∞) 1/n^s is less than 1 + ∫ (1,∞) 1/x^sdx

This follows since ∑ (n=1,∞) 1/n^s - 1 is less than ∫ (1,∞) 1/x^sdx and therefore ∑ (n=1,∞) 1/n^s is less than 1 + ∫ (1,∞) 1/x^sdx.



(4) ∫ (1,∞) 1/x^sdx = 1/(s-1)

(a) ∫ (1,∞) 1/x^sdx = lim (t → ∞) ∫ (1,t) 1/t^sdt

(b) ∫ 1/t^sdt = ∫ t^-s dt = 1/(-s+1) (t^-s+1) + C = -1/(s-1)(1/t^s-1) + C [See here for review of integral if needed]

(c) lim (t → ∞) ∫ (1,t) 1/t^sdt = lim(t → ∞) ( [-1/(s-1)][1/t^s-1] + [1/(s-1)]*[1/1^s-1])=

= lim (t → ∞) [(-1)/[(s-1)*(t^s-1)] + [1/(s-1)]*1]

(d) As t → ∞, 1/t → 0 so we get:

= [0*(-1)/(s-1)] + [1/(s-1)] = 1/(s-1)

(5) This gives us that:

1/(s-1) is less than ζ(s) is less than 1 + 1/(s-1)

(6) Multiplying (s-1) to all sides, gives us:

1 is less than (s-1)*ζ(s) is less than (s-1) + 1 = s

(7) Now as s goes to 1, it is clear that we have:

1 ≤ (s-1)*ζ(s) ≤ 1.

(8) Using the Squeeze Law (see Lemma 3, here), we can conclude that the limit is 1.

QED

References

• Harold M. Edwards, Fermat's Last Theorem: A Genetic Introduction, Springer, 2000.
  

Euler Product Formula Converges for Re(s) > 1

To move ahead on Kummer's class number formula for ideal numbers, it is necessary to review the proof for the convergence of Euler's Product Formula, that is:

∑ n^-s = ∏ (1 - p^-s)^-1

Ernst Kummer proposed an equivalent formula for ideal numbers which I will talk about in a future blog. If you are not familiar with the notation Re(s), start here.

Theorem 1: For s greater than 1, ∑ (n=1, ∞) n^-s converges absolutely.

Proof:

(1) Let σ = Re(s)

(2) abs(n^-s) = n^-σ [See Theorem, here]

(3) Let M be any integer ≥ 1.

(4) Let N be any integer greater than M

(5) Using the triangle inequality for complex numbers (See Lemma 3, here for more details) abs[∑ (n=M+1,N) n^-s)]≤ ∑ (n=M+1,N) abs(n^-s) = ∑ (n=M+1,N) n^-σ

(6) From a previous result (See Corollary 1.2, here for more details), we know that ∑ (n=M+1,N) n^-σ converges.

*(6) Since f(x)=1/x^s is positive, continuous, and decreasing for x ≥ 1, I can use a result from an earlier blog (See Corollary 1.2, here for more details) to establish that ∑ (n=M+1,N) n^-σ converges.

(7) Since all n^-s ≥ 0, we can see that it converges absolutely. [See here for definition and properties of absolute convergence]

QED

Theorem 2: For S greater than 1, ∏(1 - p^-s) converges absolutely

Proof:

(1) ∑ abs(p^-s) = ∑(p^-σ) where σ = Re(s). [See Theorem 2, here for proof]

(2) ∑(p^-σ) ≤ ∑(n^-σ) and since ∑ (n^-σ) is convergent (by Theorem 1 above), ∑ abs(p^-s) is also convergent.

(4) ∑ abs(p^-s) is convergent implies that ∏ (1 - p^-s) is convergent. [See Lemma 6, here]

(5) And this means that ∏ (1 - p^-s)^-1 is also convergent. [See Lemma 6, here]

(6) Since ∑ abs(p^-s) is convergent, it follows that ∏(1 - p^-s) is absolutely convergent and therefore ∏ (1 - p^-s)^-1 is absolutely convergent since:

(a) Assume ∑ abs(p^-s) is convergent

(b) It follows that ∏(1 - abs[p^-s]) is convergent [See Lemma 3, here]

(c) Which means that ∏(1 - p^-s) is absolutely convergent. [See Definition 1, here]

(d) Using the Reciprocal Property of limits (see Lemma 6, here), we can see that 1/∏(1 - abs[p^-s]) is also convergent.

(e) Using the definition of absolute convergence for infinite products (see step #6c above), we see that ∏ (1 - p^-s)^-1 absolutely convergent.

QED

Bernhard Riemann

Bernhard Riemann was born in the Kingdom of Hanover (now, Germany) on September 17, 1826. He was the second of six children. He was home schooled by his father, Lutheran minister, until he was 10. Through out his life, he remained very close to his family and very religious.

When he was 14, Riemann moved in with his grandmother and attended school in Lyceum. He entered the gymnasium in Luneburg in 1842. At the gymnasium, Riemann showed strong interest in mathematics. It is said that he read a 900 page book by Adrien Legendre on number theory in 6 days.

In 1846, Riemann enrolled in theology at the University of Gottingen. He continued to take classes in mathematics and later, after consulting with his father, changes his focus from theology to mathematics. At Gottingen, he was able to takes courses from the legendary mathematician Carl Friedrich Gauss.

Despite having Gauss on its faculty, the University of Gottingen was, at this time, secondary in mathematics to the University of Berlin. Riemann transferred there in 1847 and was able to attend courses in advanced mathematics given by Jakob Steiner, Carl Jacobi, Johann Dirichlet, and Ferdinand Eisenstein. These were exciting times for Riemann and he became particularly influenced by the theories of Dirichlet. It is said that at this time, Riemann built up what would become his general theory of complex variables.

Riemann returned to the University of Gottingein in 1849 to work on his Ph.D. thesis under the guidance of Gauss. Riemann was also greatly influenced by Wilhem Weber in theoretical physics and Johann Listing in topology.

Riemann's thesis was on what are today known as Riemann surfaces. In this groundbreaking work, Riemann used topology to analyze complex variables. The MacTutor biography describes this work as: "a strikingly original piece of work which examined the geometric properties of analytic functions, conformal mappings, and the connectivity of surfaces."

Today, Riemann's Ph.D. thesis is considered to be one of the most impressive that has ever been produced. Based on Gauss's recommendation, Riemann was offered a post at the University of Gottingen as a lecturer. To become a lecturer, he needed to achieve a post-doctoral degree called a Habilitation. To complete this degree, he needed to make a presentation on an advanced topic. He proposed three topics to Gauss and to his surprise, Gauss selected geometry. So, on June 10, 1854, Riemann presented a lecture on what is today known as Riemannian geometry which would later be the basis of Einstein's general theory of relativity. The lecture is today considered a classic.

The story goes that Riemann's lecture was so advanced for its time that only Gauss appreciated the depths of the ideas. While the other technical members of the audience listened politely, Gauss was greatly excited. The MacTutor biography quotes an eyewitness: "The lecture exceeded all his [Gauss's] expectations and greatly surprised him. Returning to the faculty meet, he [Gauss] spoke with the greatest phrase and rare enthusiasm to Wilhelm Weber about the depth of the thoughts that Riemann had presented."

When Gauss died in 1855, his replacement was Johann Dirichlet. In 1857, Riemann became a professor of mathematics. At this time, he wrote a paper on the theory of abelian functions. At the same time, Karl Weierstrass was working on the same topic. Riemann's paper was very advanced. Felix Klein writes: "It [Riemann's paper] contained so many unexpected, new concepts that Weierstrass withdrew his paper and in fact published no more."

In 1859, Dirichlet died and Riemann replaced him as the chair of mathematics. He was also admitted to the the Berlin Academy of Sciences. His nomination read (from MacTutor):

Prior to the appearance of his most recent work [Theory of abelian functions], Riemann was almost unknown to mathematicians. This circumstance excuses somewhat the necessity of a more detailed examination of his works as a basis of our presentation. We considered it our duty to turn the attention of the Academy to our colleague whom we recommend not as a young talent which gives great hope, but rather as a fully mature and independent investigator in our area of science, whose progress he in significant measure has promoted.

As a newly elected member of the Academy of Sciences, Riemann was expected to make a techincal presentation. Riemann's presentation unleashed what is today known as the Riemann Hypothesis. This is the most famous and most important open problem in number theory. It was identified by David Hilbert among his famous collection of 23 mathematical problems. The purpose of the paper was to outline a method for determining the number primes less than a given number.

At 36, he married Elise Koch and it seemed like his mathematical impact was only just beginning. Unfortunately, around this time, he got sick with what would later turn out to be tuberculosis. He continued to travel to Italy where he hoped a warmer environment would help his health and then returned to Gottingen. He died on July 20, 1866 in Italy.

Over all, Riemann's output was small but the influence of that output makes him one of the most influential mathematicians of the nineteenth century. He masterfully combined topics of topology, geometry, analysis, and number theory to show how each complemented the other areas. His impact on such a wide range of topics makes him one of the most important mathematicians of all time.

References

• "Bernhard Riemann", the MacTutor Biography
• John Derbyshire, Prime Obsession, Plume, 2004
  

Bernoulli Numbers and the Riemann Zeta Function

Leonhard Euler used the Bernoulli numbers to generalize his solution to the Basel Problem. This is the problem that put Euler on the map mathematically.

The Bernoulli numbers are named after Jacob Bernoulli, the same Bernoulli who popularized the Basel Problem that Euler solved. Bernoulli had been unable to solve the Basel Problem but Euler later showed how the numbers he had identified could be used to provide a general solution to ζ(2s) = ∑ n^-2s = 1/1^2s + 1/2^2s + ...

The content in today's blog is taken straight from Graham, Knuth, Patashnik's Concrete Mathematics.

The following are definitions for the hyperbolic functions. For those who would like a background on them, see here.

Definition 1: sinh z

sin h z = (e^z - e^-z)/2

Definition 2: cosh z

cosh z = (e^z + e^-z)/2

Definition 3: coth z

coth z = (cosh z)/(sinh z)

Now, we use these definitions in this lemma.

Lemma 1: z/(e^z - 1) + (z/2) = (z/2) coth (z/2)

Proof:

(1) z/(e^z - 1) + (z/2) = (2z + z[e^z - 1])/(2[e^z-1]) = (2z -z + z[e^z])/(2[e^z-1]) = (z/2)(e^z+1)/(e^{z - 1})

(2) (z/2)(e^z + 1)/(e^z-1) = [e^-(z/2)/e^-(z/2)]* (z/2)(e^z + 1)/(e^z-1) =

= (z/2)[(e^z/2 + e^-z/2)/(e^z/2 - e^-z/2)] =

= (z/2) coth (z/2)

QED

Corollary 1.1: z coth z = ∑ (n ≥ 0) 4ⁿB_2n(z²ⁿ)/(2n!)

Proof:

(1) From Lemma 1 above:

z/(e^z - 1) + (z/2) = (z/2) coth (z/2)

(2) Using a previous result (see Corollary, here), we also know that:

z/[e^z - 1] + (z/2) = ∑ (n ≥ 0)B_2nz⁽²ⁿ⁾/(2n)!

(3) Subsituting 2z for z gives us:

(2z)/(e^2z - 1) + z = z coth z = ∑ (n ≥ 0)B_2n(2z)⁽²ⁿ⁾/(2n)! =

= ∑ (n ≥ 1)(4)ⁿB_2n(z)⁽²ⁿ⁾/(2n)!

QED

Lemma 2: cot x = i coth ix

Proof:

(1) e^ix = i sin x + cos x [See Euler's Formula Theorem, here]

(2) cosh ix = (e^ix + e^-ix)/2 = (isinx + cos x + isin(-x) + cos(-x))/2 = 2cos(x)/2 = cos(x)

(3) sinh ix = (e^ix - e^-ix)/2 = (isin x + cos x - isin(-x) -cos(-x))/2 = 2isin(x)/2 = isin(x)

(4) i coth ix = i (cosh(ix)/sinh(ix)) = i ( cos(x)/isin(x)) = cot(x)

QED

Lemma 3: z cot z = ∑ (n ≥ 0) (-4)ⁿB_2n(z²ⁿ)/(2n)!

where B_i is a Bernoulli number [See Definition 1, here for definition of Bernoulli numbers]

Proof:

(1) From Corollary 1.1 above, we have:

z coth z = ∑ (n ≥ 0)B_2n(2z)⁽²ⁿ⁾/(2n)!

(2) Using Lemma 2 above, we have:

z cot z = ∑ (n ≥ 0)B_2n(2iz)⁽²ⁿ⁾/(2n)! =

= ∑ (n ≥ 1)(-4)ⁿB_2n(z)⁽²ⁿ⁾/(2n)!

QED

Lemma 4: cot z = (1/2ⁿ) ∑ (k=0, 2ⁿ-1) cot ([z + kπ]/2ⁿ)

Proof:

(1) I will use induction for this proof.

(2) For n=1, we have:

cot z = (1/2) cot(z/2) + (1/2) cot(z/2 + π/2)

(a) Since cot(z/2 + π/2) = - tan(z/2) [See Corollary 1.6, here], we have:

(1/2)cot(z/2) + (1/2)cot(z/2 + π/2) = (1/2)[cot(z/2) - tan(z/2)] = (1/2)[cos(z/2)/sin(z/2) - sin(z/2)/cos(z/2)] = (1/2)[cos²(z/2) - sin²(z/2)]/[sin(z/2)cos(z/2)]

(b) Since cos(z) = cos²(z/2) - sin²(z/2) [see Lemma 3, here], we have:

cot z = (1/2)[cos(z)]/[sin(z/2)cos(z/2)]

(c) Since sin(2x) = 2sin(x)cos(x) [See Lemma 2, here], we have:

cot z = (1/2)[cos(z)/[(1/2)sin(z)]] = cos(z)/sin(z) = cot z

(3) Assume that cot z = (1/2ⁿ) ∑ (k=0, 2ⁿ-1) cot ([z + kπ]/2ⁿ) for n ≥ 1.

(4) Using cot(2x) = (1/2)[cot(x) - tan(x)] [See Corollary 3.6, here], we have:

cot z = (1/2ⁿ) ∑ (k=0, 2ⁿ-1) cot ([z + kπ]/2ⁿ) =

= (1/2ⁿ⁺¹) ∑ (k=0,2ⁿ-1) [ cot([z + kπ]/2ⁿ⁺¹) - tan(z + kπ]/2ⁿ⁺¹) ]

(5) Since -tan(x) = cot(x + π/2), we have:

cot z = (1/2ⁿ⁺¹) ∑ (k=0,2ⁿ-1) [ cot([z + kπ]/2ⁿ⁺¹) + cot(z + kπ]/2ⁿ⁺¹ + π/2) ] =

(1/2ⁿ⁺¹) ∑ (k=0,2ⁿ-1) [ cot([z + kπ]/2ⁿ⁺¹) + cot(z + (k+ 2ⁿ)π]/2ⁿ⁺¹) ] =

(1/2ⁿ⁺¹) ∑ (k=0,2ⁿ-1) cot([z + kπ]/2ⁿ⁺¹) + (1/2ⁿ⁺¹) ∑ (k=0,2ⁿ-1) cot([z + (k + 2ⁿ)π]/2ⁿ⁺¹) =

= (1/2ⁿ⁺¹) ∑ (k=0,2ⁿ-1) cot([z + kπ]/2ⁿ⁺¹) + (1/2ⁿ⁺¹) ∑ (k=2ⁿ,2ⁿ⁺¹-1) cot([z + kπ]/2ⁿ⁺¹) =

= (1/2ⁿ⁺¹) ∑ (k=0, 2ⁿ⁺¹-1) cot ([z + kπ]/2ⁿ⁺¹)

QED

Corollary 4.1: cot z = (1/2ⁿ) cot (z/2ⁿ) - (1/2ⁿ) tan (z/2ⁿ) + ∑ (k=1, 2^n-1-1) (1/2ⁿ) (cot[(z + kπ)/2ⁿ] + cot[(z - kπ)/2ⁿ])

Proof:

(1) From Lemma 4, substituting (n-1) for (n), we get:

cot z = (1/2^n-1) ∑ (k=0, 2^n-1-1) cot ([z + kπ]/2^n-1) =

= (1/2^n-1) cot(z/2^n-1) + (1/2^n-1) ∑ (k=1, 2^n-1-1) cot([z + kπ]/2^n-1)

(2) Using cot(2x) = (1/2)[cot(x) - tan(x)] (see Corollary 3.6, here), we get:

(1/2^n-1) cot(z/2^n-1) = (1/2ⁿ)[cot(z/2ⁿ) - tan(z/2ⁿ)]

(3) We also get:

(1/2^n-1) ∑ (k=1, 2^n-1-1) cot([z + kπ]/2^n-1) = (1/2ⁿ) ∑ (k=1, 2^n-1-1) [cot([z + kπ]/2ⁿ) - tan([z+kπ]/2ⁿ)]

(4) To complete the proof, we just need to show that ∑ (k=1, 2^n-1-1) -tan([z+kπ]/2ⁿ) = ∑ (k=1, 2^n-1-1) cot([z - kπ]/2ⁿ)

(5) First, we note that -tan(z) = cot(z - π/2) since:

-tan(z) = cot(z + π/2) = cot(z - π + π/2) = cot(z - π/2) [See Corolary 1.6 and Corollary 1.5, here]

(6) This gives us that:

∑ (k=1, 2^n-1-1) -tan([z + kπ]/2ⁿ) = ∑(k=1,2^n-1-1) cot([z + kπ]/2ⁿ - π/2) =

= ∑ (k=1,2^n-1-1) cot([z + (-2^n-1 + k)π]/2ⁿ)

(7) Now we can see that -2^n-1 + k = -1 when k=2^n-1-1 and -2^n-1 + k = -2^n-1+1 when k = 1.

(8) Therefore:

∑ (k=1,2^n-1-1) cot([z + (-2^n-1 + k)π]/2ⁿ) = ∑ (k=1,2^n-1-1) cot([z - kπ]/2ⁿ)

QED

Lemma 5: lim (z → 0) z cot z = 1

Proof:

(1) lim(z → 0) z cot z = lim(z → 0) cos(z)* lim(z → 0) (z/sin(z)) [By Product Rule for Limits, see Lemma 2, here]

(2) lim(z → 0) cos(z) = 1 [See Property 6, here if needed]

(3) lim (z → 0) (z/sin(z)) = lim(z → 0) 1/(sin(z)/z) [By the Reciprocal Law for Limits, see Lemma 6 here]

(4) lim (z → 0) (sin(z)/z) = 1 [See Lemma 2, here]

(5) Putting it all together gives us:

lim (z → 0) z cot z = lim(z → 0) cos(z) * 1/[lim(z → 0) sin(z)/z] = 1*(1/1) = 1

QED

Corollary 5.1: z cot z = 1 - 2 ∑ (k ≥ 1) z²/[k²π² - z²]

Proof:

(1) Using Corollary 4.1 above, we have:

z cot z = (z/2ⁿ) cot (z/2ⁿ) - (z/2ⁿ) tan (z/2ⁿ) + ∑ (k=1, 2^n-1-1) (z/2ⁿ) (cot[(z + kπ)/2ⁿ] + cot[(z - kπ)/2ⁿ])

(2) Since n can take any value, we can see that:

z cot z = lim (n → ∞) [ (z/2ⁿ) cot (z/2ⁿ) - (z/2ⁿ) tan (z/2ⁿ) + ∑ (k=1, 2^n-1-1) (z/2ⁿ) (cot[(z + kπ)/2ⁿ] + cot[(z - kπ)/2ⁿ]) ]

(3) As n approaches ∞, z/2ⁿ approaches 0, so that using Lemma 5 above we have:

lim(n → ∞) (z/2ⁿ)cot(z/2ⁿ) = lim (z → 0) (z) cot(z) = 1

(4) Likewise,

lim(n → ∞) -(z/2ⁿ)tan(z/2ⁿ) = lim(z → 0) -z*tan(z) = lim(z → 0) (-z) * sin(z)/cos(z) = (-z)*(0)*(1) = 0 [See Product Rule for Limits for details if needed, see Lemma 2, here]

(5) Now, (z/2ⁿ) = [(z + kπ)/2ⁿ]*[z/(z + kπ)] so that:

lim(n → ∞) (z/2ⁿ)*cot([z + kπ]/2ⁿ) =

lim(n → ∞) [z/(z + kπ)]*[(z+kπ)/2ⁿ]*cot([z + kπ]/2ⁿ)

(6) Let u = (z + kπ)/2ⁿ

(7) As n → ∞, u → 0, so that we have:

lim(n → ∞) (z/2ⁿ)*cot([z + kπ]/2ⁿ) =
lim(u → 0) [z/(z + kπ)]*u*cot(u) = [z/(z + kπ)]*1 = z/(z + kπ)

(8) Let v = (z - kπ)/2ⁿ

(9) As n → ∞, v → 0, so that we have:

lim(n → ∞) (z/2ⁿ)*cot([z - kπ]/2ⁿ) =
lim(v → 0) [z/(z - kπ)]*v*cot(v) = [z/(z - kπ)]*1 = z/(z - kπ)

(10) So, lim (n → ∞) [ (z/2ⁿ)cot([z + kπ]/2ⁿ) + (z/2ⁿ)cot([z - kπ]/2ⁿ) = z/(z + kπ) + z/(z - kπ) = [z*(z - kπ) + z(z + kπ)]/(z² - k²π²) = (2z²)/(z² - k²π²) [See Addition Rule for Limits, see Corollary 8.1, here]

(11) Finally,

lim (n → ∞) (z/2ⁿ) cot (z/2ⁿ) - (z/2ⁿ) tan (z/2ⁿ) + ∑ (k=1, 2^n-1-1) (z/2ⁿ) (cot[(z + kπ)/2ⁿ] + cot[(z - kπ)/2ⁿ]) =

= 1 - 0 + ∑(k ≥ 1) 2z²/(z² - k²π²) = 1 - 2*∑ (k ≥ 1) z²/(k²π² - z²)

QED

Lemma 6: z²/[k²π² - z²] = ∑ (i ≥ 1) z²ⁱ/[k²ⁱπ²ⁱ]

Proof:

(1) 1/(1 - x) = 1 + x + x² + ... [See Lemma 1, here]

(2) x/(1 - x) = x + x² + x³ + ...

(3) Let x = (z²)/(k²π²)

(4) Then:

[(z²)/(k²π²)]/[1 - (z²)/(k²π²)] =

(z²)/[(k²π²](1 - (z²)/(k²π²)] =

= z²/(k²π² - z²)

QED

Theorem: ζ(2n) = (-1)^n-1[2^2n-1π²ⁿB_2n]/(2n)!

where:

ζ(s) = 1/1^s + 1/2^s + 1/3^s + ...

B_i is a Bernoulli number

Proof:

(1) z cot z = 1 - 2 ∑ (k ≥ 1) z²/[k²π² - z²] [See Lemma 5 above]

(2) Using Lemma 6 above, we have:

z cot z = 1 - 2∑ (k ≥ 1)[ z²/k²π² + z⁴/k⁴π⁴ + z⁶/k⁶π⁶ + ... ]

(3) Since for each of term of this sum, k can take all integer values ≥ 1, we replace the ∑(k ≥ 1) with:

z cot z = 1 - 2(z²ζ(2)/π² + z⁴ζ(4)/π⁴ + z⁶ζ(6)/π⁶ + ...

(4) From Lemma 3 above, we have:

z cot z = ∑ (n ≥ 0) (-4)ⁿB_2n(z²ⁿ)/(2n)! = B₀ + ∑ (n ≥ 1) (-4)ⁿB_2n(z²ⁿ)/(2n)! =
= 1 + ∑ (n ≥ 1) (-4)ⁿB_2n(z²ⁿ)/(2n)!

(5) Equating the equations in step #3 and step #4 gives us:

- 2(z²ζ(2)/π² + z⁴ζ(4)/π⁴ + z⁶ζ(6)/π⁶ + ... = ∑ (n ≥ 1) (-4)ⁿB_2n(z²ⁿ)/(2n)!

(6) This gives us for each term i ≥ 1:

-2z^2*iζ(2*i)/π^2*i = (-4)ⁱB_2i(z²ⁱ)/(2i)!

(7) Solving for ζ(2*i), this gives us:

ζ(2i) = (-4)ⁱB_2iπ²ⁱ/[(2i)!(-2)] =

= (-1)^i-1(2^2i-1π²ⁱB_2i)/(2i)!

QED