Scipione del Ferro's great discovery which eventually led to the general solution of the cubic equation was the solution of the depressed cubic equation:
x3 + bx = c
In today's blog, I will show how del Ferro solved this equation. The content is taken from Paul J. Nahin's
The Story of √-1
(1) Let
x = u+v
(2) Then:
x3 + bx = (u + v)3 + b(u + v) =
= u3 + 3u2v + 3uv2 + v3 + b(u + v) =
= u3 + v3 + (3uv + b)(u + v) = c
(3) Now, if:
(3uv + b) = 0
then:
u3 + v3 = c
(4) Now,
(3uv + b) = 0 → 3uv = -b
and further:
v = -b/(3u)
(5) So if:
u3 + v3 = c, then:
u3 + [-b/(3u)]3 - c =
u3 + (-b3)/(27u3) - c =
u6 + (-b3/27 - cu3 = 0
(6) But this is an example of a quadratic equation since if:
z = u3, then we have:
u6 + (-b3/27) - cu3 =
= z2 - cz -(b3/27)
(7) Using the solution for the quadratic equation (see
here), we have:
z
= (c/2) ± √c2 - 4(-b3/27)/2 =
=(c/2) ± √c2/4 + b3/27 = u3
(8) Considering only the positive form, we have:
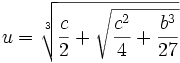
(9) Since
v3 = c - u3, we have:
v
3 = c - (c/2 + √
c2/4 + b3/27 =
= c/2 - √
c2/4 + b3/27
(10) This then gives us:
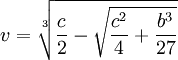
(11) Since
x = u + v, this gives us that:
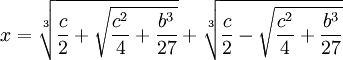
(12) Since
(-1)3 = (-1)

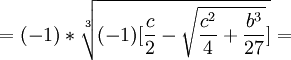
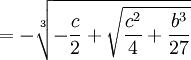
(13) This tells us that we can restate (11) as the following:
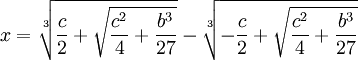
In another blog, I present
a proof that this really is the solution of the depressed cubic.
References
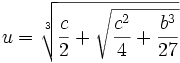 (9) Since v3 = c - u3, we have:
v3 = c - (c/2 + √c2/4 + b3/27 =
= c/2 - √c2/4 + b3/27
(10) This then gives us:
(9) Since v3 = c - u3, we have:
v3 = c - (c/2 + √c2/4 + b3/27 =
= c/2 - √c2/4 + b3/27
(10) This then gives us:
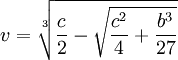 (11) Since x = u + v, this gives us that:
(11) Since x = u + v, this gives us that:
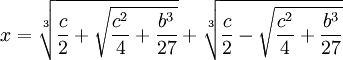 (12) Since (-1)3 = (-1)
(12) Since (-1)3 = (-1)

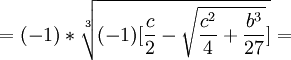
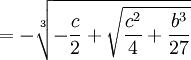 (13) This tells us that we can restate (11) as the following:
(13) This tells us that we can restate (11) as the following:
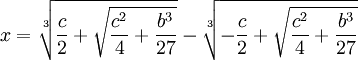 In another blog, I present a proof that this really is the solution of the depressed cubic.
References
In another blog, I present a proof that this really is the solution of the depressed cubic.
References

9 comments:
Hi there,
I found your explanation very useful for solving cubic equation. Up to step 11, I followed it well. But in Step 12, I could not understand why -1 (cube) calculation happened. Also, my intent was to find out the roots for a cubic equation. If you could add some details on finding the roots for a cubic equation (not just the depressed cubic), it will be very helpful - Ram from Bangalore, India
One additional point, what I am trying to figure out is; why should I restate 11 and 13. Now, I followed the step 12 (i.e.) 1 was termed as -1 * -1 and then -1 was brought into the cubic root. and thus 11 was equated with 13. But how does the equation help. What purpose does it serve?fvu
Hi Ramanathan,
Thanks very much for your question.
As you point out accurately, the two equations step #11 and step #13 are equivalent.
I present both steps just to show that they are equal to each other.
In books about the depressed cubic, they might show the equation in #11 or the equation in #12.
If you are interested in seeing the full proof for the cubic equation, I have a blog on it here.
Cheers,
-Larry
i want to find the solution of the eq 8x^3-6x+=0
how to solve the cubic equations of form Ax^3-Bx+C=0
i ve been trying to solve the eq 8x^3-6x+1=0 but havent got any success so far
Great, a much clearer method to follow than in Nahins book. Thanks for taking the time to do this.
I am researching about the history of imaginary numbers for a presentation and as far as I have learnt from internet, this proof belongs to Cardana ( from the book Ars Magna ) and it is said in [1] that as a result of learning Ferro knew the proof before him, he has mentioned Ferro as the first author to his book.
[1] http://www.math.uri.edu/~merino/spring06/mth562/ShortHistoryComplexNumbers2006.pdf
Also I have seen in various places that this proof is attributed to Cardano. Tell me if you know more please
I took my details from wikipedia and history of math books. If your sources are authoritative and current, then I may need to change the details of ny blog. I will take a look. Thanks for your question!
Post a Comment