For an equation of the form x3 + bx2 + cx + d = 0, Cardano did this by setting x = y - b/3.
The solution is complicated. Still, this solution was a very important step forward past the mathematics of Ancient Greece. Additionally, it would lead eventually to the acceptance of imaginary numbers and the establishment of group theory.
Lemma 1: Cardano's simplification of general cubic equation
If:
x3 + bx2 + cx + d = 0
Then there exists y,p,q such that:
y3 + py + q = 0
Proof:
(1) x3 + bx2 + cx + d = 0
(2) Let y = x + b/3
(3) Then, x = y - b/3
(4) x3 = (y - b/3)3 = y3 - 3by2/3 + 3b2y/9 - b3/27 =
= y3 - by2 + b2y/3 - b3/27
(5) bx2 = b(y - b/3)2 = by2 - 2b2y/3 + b3/9
(6) x3 + bx2 = y3 - b2y/3 + 2b3/27
(7) x3 + bx2 + cx + d =
= y3 - b2y/3 + 2b3/27 + c(y - b/3) + d =
= y3 + (c - b2/3)y + (2b3/27 - bc/3 + d)
(8) Let:
p = c - b2/3
q = 2b3/27 - bc/3 + d
QED
Theorem: Solution to General Cubic Equation
If:
ax3 + bx2 + cx + d = 0
Then:
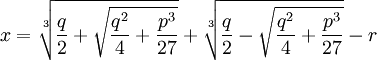
where:
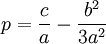
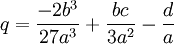
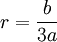
Proof:
(1) ax3 + bx2 + cx + d = 0
(2) If we divide all sides by a, we get:
x3 + (b/a)x2 + (c/a)x + (d/a) = 0
(3) Then using Lemma 1 above, if we set:
y = x - (b/a)/3
p = (c/a) - (b/a)2/3
q = -2(b/a)3/27 + (b/a)(c/a)/3 - (d/a)
Then we have:
y3 + py - q = 0
or:
y3 + py = q
(4) Now, using the solution for the depressed cubic (see Theorem, here),
we have:
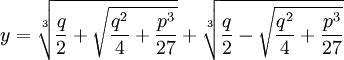
(5) Finally, adjusting for step #3, if we let:
r = (b/a)/3
Then we have:
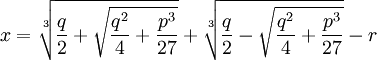
QED

1 comment:
This doesn't always work... if you have the equation x^3-6x^2+11x-6=0, the formula should produce x=1, yet your proof provides that the formula results in 1.92264973081037 + 0.288675134594813*i. The problem is that your determinant is negative and introducing a complex number in the intermediate steps of the formula.
Post a Comment