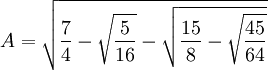François Viète was born in 1540 in France; he was a successful politician who also made very important contributions to algebra. He is credited for example with introducing letters to represent known and unknown values in mathematical equations. His writings were also important in establishing the symbol (+) as representing addition and (-) as representing subtraction.
His family was well connected; his mother, for example, was the first cousin of the president of Parliament in Paris. Viète was able to take advantage of these connections through out his life. He attended the University of Poitiers and in 1560, he graduated with a law degree.
Although a lawyer by profession, he took a strong interest in math and science and published his first mathematical paper in 1571. He was especially interested in the works of
Pappus and
Diophantus.
Viète was a
Huguenot and he lived in Paris during the
St. Bartholomew's Day Massacre where many thousands of protestant Hugeuenots were killed.
In 1573, he became a councillor at Rennes where he remained until 1580. At that time, he was appointed by
King Henry III to be a royal privy councillor in Paris. In 1584, King Henry III's younger brother became ill and died; this meant that
Henry of Navarre, a protestant, became heir to the throne. In the struggle that erupted, Viète, a protestant, was kicked out of office.
Viète left Paris and headed to the small town of Beauvoir-sur-Mer. He spent five years there where he was able to devote time to studying mathematics. It was during this time that he did most of his most imporant work relating to cubic equations and mathematical notation.
Viète believed that the Greeks had not revealed all their mathematical insights. He believed that they had secret methods which he hoped to rediscover. In this way, he introduced what would later become variables and coefficients. In Viète's view, he had restored the hidden mathematical methods of the Greeks.
In 1589, he was called back to parliament in Tours. This happened just before Henry III was assassinated on August 1, 1589. He stayed on as the protestant Henry of Navarre became King Henry IV.
In 1590, a coded letter to
King Philip II of Spain was intercepted by the French. Viète, at this time, had a very strong reputation in mathematics and he was given the task of deciphering the note. This he accomplished in March of 1590. The MacTutor web site quotes a historical text:
... when Philip, assuming that the cipher could not be broken, discovered that the French were aware of his military plans, he complained to the Pope that black magic was being employed against his country.
When in 1592, King Henry IV converted to Catholicism. Viète did the same.
In 1593, there was a challenge made to all mathematicians by
Adriaan van Roumen, a professor of math at Louvain. Roumen asked for a solution to an equation which had 45 terms. Viète was able to solve this problem. In fact, Roumen asked for one solution. Viète was able to demonstrate that there were 23 positive solutions.
Viète was very wealthy. He published all of his writings himself and sent them out to scholars throughout Europe. In all of his writings, he only focuses on positive values. Like many of the mathematicians before him, he did not include consideration of negative numbers in his writings.
He was a member of the Royal Privy Council until his death in February, 1603.
References
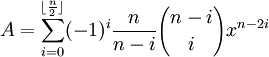
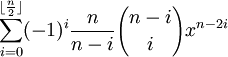
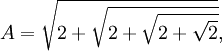

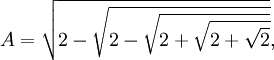

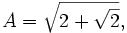

, World Scientific, 2001