The content in today's blog is taken straight from Harold M. Edwards' Galois Theory.
Theorem 1: Fundamental Theorem on Symmetric Polynomials
Every symmetric polynomial in r1, ..., rn can be expressed as a polynomial in elementary symmetric polynomials σ1, ..., σn. In addition, a symmetric polynomial with integer coefficients can be expressed as a polynomial in elementary symmetric polynomials with integer coefficients.
Proof:
(1) For n=1, the symmetric polynomial is x - r1 so that we see that a1 = -r1 and σi = (-1)1(-r1)=r1
[See Definition 1, here for definition of symmetric polynomial; see Definition 2, here for definition of the kth elementary symmetric polynomial]
(2) if a1 is an integer, then r1 is an integer and σ1 is an integer.
(3) The polynomial in elementary symmetric functions is then x - σ1 which shows that the theorem is true for n=1.
(4) Let's assume that the theorem has been proved for all symmetric polynomials up to n-1.
(5) Let G(r1, r2, ..., rn) be a symmetric polynomial in n variables so that:
G(r1, r2, ..., rn) = (x - r1)*(x - r2)*...*(x - rn)
(6) Let Gi be a series of polynomials such that:
G(r1, r2, ..., rn) = G0 + G1rn + G2(rn)2 + ... + Gv(rn)v
where:
v is the highest power of rn that occurs in G and each Gi is only made up of r1, r2, ..., rn-1.
We can see that G0 is a polynomial that doesn't include rn. G1 includes all multiples of (rn)1. G2 includes all the multiples of (rn)2 and so on up until v which is defined as the highest power of rn which can be 1.
(7) Now, since G(r1, r2, ..., rn) is a symmetric polynomial, it is unchanged if any two variables ri and rj are interchanged. [See Definition 1 here for definition of symmetric polynomial]
(8) Since G(r1, r2, ..., rn) is unchanged with any interchange, so too are the polynomials defined by Gi are unchanged.
(9) This means that each Gi is itself a symmetrical polynomial on r1, r2 ... rn-1.
(10) By the inductive hypothesis in step #4, we can assume that each Gi is itself expressible as an elementary symmetric polynomial in r1, r2, ..., rn-1
(11) Let τi, τ2, ..., τn-1 denote these elementary polynomials in (n-1) variables such that [See Definition 2 here for definition of elementary symmetric polynomials]:
τ1 = r1 + r2 + ... + rn-1
τ2 = r1r2 + r1r3 + ... + rn-2rn-1
...
τn-1 = r1r2*...*rn-1
[NOTE: Each τi represents the sum of all i-combinations of 1 ... n-1. So, τ1 is the sum of all 1-combinations, τ2 is the sum of all 2-combinations, and τn-1 is the sum of all n-1 combinations (for which there is only one)].
(12) So, from the inductive hypothesis, if we let Gi(r1, ..., rn-1) represent the symmetric polynomial Gi, we can see that there exists another polynomial gi such that:
Gi(r1, ..., rn-1) = gi(τ1, τ2, ..., τn-1)
(13) Further, from the inductive hypothesis, we know that if Gi has integer coefficients, then, so does gi.
(14) Let σ1, σ2, ..., σn be the elementary symmetric polynomials in n variables.
(15) We can now restate σi in terms of τi since:
σ1 = r1 + r2 + ... + rn = τ1 + rn
σ2 = r1r2 + r1r3 + ... + rn-1rn = τ2 + rnτ1
[Note: rn*τ1 is equal to the sum of all (n-1) 1-combinations with rn]
σ3 = r1r2r3 + r1r2r4 + ... + rn-2rn-1rn = τ3 + rnτ2
[Note: rn*τ1 is equal to the sum of all (n-1) 2-combinations with rn]
σ4 = τ4 + rnτ3
...
σn = r1*r2*....*rn = 0 + rn*tn-1
[Note: the main idea here is the σi represents the sum of all i-combinations of n variables. We are now equating these sums with τi which represents the sum of all i-combinations of (n-1) variables. In other words, we are now including the new combinations with rn.]
(16) We can now restate the equations in step #15 in terms of τi to get (using the basic algebraic operations of addition/subtraction to both sides of the equation):
τ1 = σ1 - rn
τ2 = σ2 - rnτ1 = σ2 - rn(σ1 - rn) = σ2 - rnσ1 + (rn)2
τ3 = σ3 - rnτ2 = σ3 - rnσ2 + (rn)2σ1 - (rn)3.
...
τn-1 = σn-1 - rnτn-2 = σn-1 - rnσn-2 + ... + (-1)n-1(rn)n-1
(17) Finally, we can use the last equation in step #15, to get:
0 = σn - rnτn-1 = σn - rnσn-1 + ... + (-1)n(rn)n.
(18) Since we restate all the terms τi in terms of rn and σi, we can define a polynomial fi(σ1, σ2, ..., σn-1), such that using step # 12, we have:
G(r1, r2, ..., rn) = f0 + f1(σn) + f2(σn)2 + ... + fμ(σn)μ
where each fi is a polynomial strictly in terms of σ1, σ2, ..., σn-1 and does not include σn.
(19) Each fi has integer coefficients if G does since:
(a) Using steps #16, we can state each fi in terms of τ1,...,τn-1
(b) From step #13, we know that τ1,...,τn-1 have integer coefficients if G has.
(20) From step #17, we get the following:
(rn)n = (rn)n-1σ1 - (rn)n-2σ2 + (rn)n-3σ3 + ... + (-1)n-1σn
(21) If μ ≥ n, then we can continuously apply the result in step #18 to the result in step #20, to get:
G(r1, r2, ..., rn) = f0(σ) + f1(σ)rn + f2(σ)(rn)2 + ... + fn-1(σ)(rn)n-1
(22) Since interchanging any values ri with rj doesn't change the value of G(r1, r2, ..., rn), then it doesn't change the value of f0(σ) + f1(σ)rn + f2(σ)(rn)2 + ... + fn-1(σ)(rn)n-1
(23) By repeatedly interchanging distinct ri and rj values where i ≠ j, we get the following n set of equations using step #21:
G(r1, r2, ..., rn) = f0 + f1r1 + f2(r1)2 + ... + fn-1(r1)n-1
G(r1, r2, ..., rn) = f0 + f1r2 + f2(r2)2 + ... + fn-1(r2)n-1
...
G(r1, r2, ..., rn) = f0 + f1rn + f2(rn)2 + ... + fn-1(rn)n-1
(24) We can think of these n equations of n terms as an n x n matrix of the form (ri)j-1 where i = the column (1 ... n) and j = the row (1 ... n).
(25) The determinant of this matrix which is a polynomial in r1, r2, ..., rn is nonzero since this is an example of the transpose of the Vandermonde Matrix [see Definition 1, here] and:
(a) From the properties of determinants, we know that det(Vn) = det(VnT) [See Theorem 9, here]
(b) The formula for the determinant of the Vandermonde matrix is (see Theorem 1, here):


(c) Since by assumption r1 ≠ r2 ≠ ... ≠ rn [since each of the parameters is distinct], we can conclude that det(Vn) ≠ 0.
(26) We can think of the set of equations as a multiplication between the above matrix [(ri)j-1] and the vector [f0(σ), f1(σ), ..., fn-1(σ)] [See here for review of matrix multiplication] since:


(27) But, the the set of equations is also the result of multiplying the vector[G,0,0,...,0] since:
(a) We have the following equation:
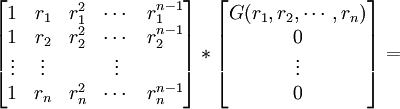

(b) From step #23, we have:

=

(c) So we can conclude that the following two equations are equal:


(28) Since the determinant in step #24 above is nonzero, the matrix is invertible (see Theorem 4, here) and we can multiply its inverse to both sides to get:

(29) From this, we can conclude that:
f0 = G and f1=0, ..., fn-1=0. [See Definition 2, here]
(30) Since f0 is an elementary symmetric polynomial (see step #18 above) and since f0 has integer coefficients if G does (see step #19 above), the conclusion follows from mathematical induction (see here for review of mathematical induction).
QED
In my next blog, I will complete the proof by reviewing the formula for the determinant of the Vandermonde Matrix. In a future blog, I will show how this theorem can be used to derive Newton's identities.
References
- Harold M. Edwards, Galois Theory, Springer, 1984.

