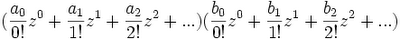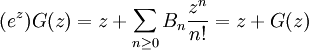The content in today's blog is taken from Concrete Mathematics (Graham, Knuth, and Patashnik, 1989).
Definition 1: Bernoulli Polynomial
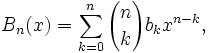
where n ≥ 0 and bk is the Bernoulli number (see Definition 1, here)
I will now show how Bernoulli Polynomials can be used to create a concise summation formula.
Lemma 1: ∑ (k=0,n) ekz = [enz - 1]/[ez - 1]
Proof:
(1) Let Sn = ∑ (k=0,n-1) ekz = ∑ (k=0, n) (ez)k = e0 + ez + e2z + ... + e(n-1)z
(2) Sn + (ez)n = (ez)0 + ∑ (k=0,n-1) (ez)k+1
(3) (ez)Sn = (ez)∑ (k=0,n-1) (ez)k = ∑ (k=0,n) (ez)k+1
(4) Putting #2 and #3 together gives us:
Sn + (ez)n = (ez)Sn + 1
(5) So, solving for Sn gives us:
Sn - (ez)Sn = 1 - (ez)n = Sn(1 - ez)
(6) Dividing both sides by (1 - ez) gives us:
Sn = [1 - (ez)n]/[1 - ez] *(-1)/(-1) = [enz - 1]/[ez - 1]
QED
NOTE: If you are not familiar with the idea of generating functions, start here.
Corollary 1.1: Generating Function for Bernoulli Polynomials
∑ (m ≥ 0) Bm(n)zm/m! = (zexz)/(ez - 1)
Proof:
(1) Let T(z,n) be the generating function for Bernoulli polynomials Bm(n) so that we have:
T(z,n) = B0(n)z0/0! + B1(n)z1/1! + .... = ∑ (m=0,∞) Bm(n)zm/m!
(2) Inserting the definition for Bernoulli polynomials (see Definition1 above), we have:
T(z,n) = ∑ (m=0,∞) ∑(k=0; m) [(m!/[k!][m-k]!)*Bkxn-k] zm/m!
(3) Using a previous result on binomial convolution (see Lemma 1, here), we can reverse this to get:
∑(m=0; ∞) ∑(k=0;m) [(m!/[k!][m-k]!)*Bkxn-k] zm/m! = [∑(m=0; ∞) Bmzm/m!]*[∑(m=0, ∞) xmzm/m!]
(4) From a previous result (see Theorem, here), we have:
∑ (m ≥ 0) (Bm)zm/m! = z/[ez - 1]
(5) Further, using the power series for e (see Lemma 2, here), we have:
exz = ∑ (m ≥ 0) xmzm/m!
(6) Inserting these results gives us:
T(z,n) = ∑(m=0; ∞) ∑(k=0;m) [(m!/[k!][m-k]!)*Bkxn-k] zm/m! = [∑(m=0; ∞) Bmzm/m!]*[∑(m=0, ∞) xmzm/m!] =
= (z/[ez - 1])*(exz) = (zexz)/(ez - 1)
QED
Theorem: Sm-1(n) = (1/m)(Bm(n) - Bn(0))
Proof:
(1) Sm(n) = 0m + 1m + ... + (n-1)m = ∑ (k=0,n) km [See Definition2, here for definition of Sm(n)]
(2) Let S(z) = ∑ (m ≥ 0) Sm(n) zm = S0(n) + S1(n)z + S2(n)z2 + ... = ∑ (m ≥ 0) ∑ (k=0,n) kmzm
(3) Using the power series for ez (see Lemma 2, here), we know that:
ez = ∑ (n ≥ 0) zn/n! = z0/0! + z1/1! + ... + zn/n!
(4) We can see that:
ekz = ∑ (m ≥ 0) (kz)m/m! = ∑(m ≥ 0)kmzm/m!
(5) Let G(z,n) be the generating function for S(z) so that we have:
G(z,n) = S0(n)x0/0! + S1(n)z1/1! + S2(n)/z2/2! + ... = ∑ (m ≥ 0) Sm(n)zm/m!
(6) Using step #2, then we have:
G(z,n) = ∑ (m ≥ 0) ∑ (k=0, n) kmzm/m! = ∑ (k=0,n) ekz
(7) Using the Lemma 1 above, we have:
G(z,n) = [enz - 1]/[ez - 1]
(8) Let T(z,n) be the generating function for the Bernoulli Polynomial
(9) Using Corollary 1.1 above, we have:
T(z,n) = ∑ (m ≥ 0) Bm(n)zm/m! = (zexz)/(ez - 1)
(10) This then gives us that:
T(z,n) - T(z,0) = (zenz)/(ez - 1) - (ze0z)/(ez - 1) = z[enz - 1]/[ez-1]
(11) This shows that z*G(z,n) = [T(z,n) - T(z,0)]
(12) So that we have:
S0(n)z1/0! + S1(n)z2/1! + S2(n)/z3/2! + ... = [(B0(n)z0/0! + B1(n)z1/1! + ....) - (B0(0)z0/0! + B1(0)z1/1! + ....)]
(13) Lining up, equal powers of zi gives us:
Sm-1(n)/(m-1)! = Bm(n)/m!] - Bm(0) /m!
(14) Multiplying both sides by (m-1)! gives us:
Sm-1(n) = (1/m)[Bm(n) - Bm(0)]
QED
References
- "Bernoulli Polynomials", Wikipedia.com
- Ronald L. Graham, Donald E. Knuth, Oren Patashnik, Concrete Mathematics, Addison-Wesley, 1989