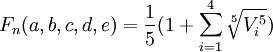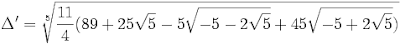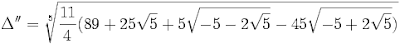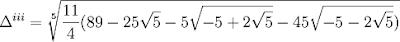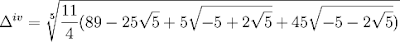In today's blog, I will show how
Alexandre-Theophile Vandermonde solved the eleventh root of unity by radicals.
Carl Friedrich Gauss would later generalize this result to show that all n-th roots of unity are expressible as radicals. I will go through Gauss' results in a future blog.
Lemma 1:if
a,b,c,d,e are the roots of:
x5 - x4 - 4x3 + 3x2 + 3x - 1 = 0then:
a + b + c +d + e = 1Proof:
(1) Using the Fundamental Theorem of Algebra (see Theorem,
here), we know that:
x5 - x4 - 4x3 + 3x2 + 3x - 1 = (x - a)(x - b)(x - c)(x -d)(x -e)(2) From this it is clear that the coefficient for
x4 is the sum of
-ax4 + -bx4 + -cx4 + -dx4 + -ex4Thus, we have:
-1(x4) = -ax4 + -bx4 + -cx4 + -dx4 + -ex4(3) Dividing
-x4 from both sides gives us:
1 = a + b + c + d + eQED
Lemma 2:If:
a2 = -b + 2b2 = -d + 2c2 = -e + 2d2 = -c + 2e2 = -a + 2and
ab = -a -cbc = -a -ecd = -a -dde = -a-bac = -b -dbd = -b -ece = -b -cad = -c - ebe = -c -dae = -d -eThen:
(ρ1ia + ρ2ib + ρ3ic + ρ4id + ρ5ie)n = Aa + Bb + Cc +Dd + Ee + Fwhere
A,B,C,D,E,F are functions consisting solely of combinations of
ρki (it does not include
a,b,c,d or
e)
Proof:
(1) The statement is clearly true for
n=1.
(2) Assume that it is true up to some
n-1 so that we have:
(Aa + Bb + Cc +Dd + Ee) *(ρ1ia + ρ2ib + ρ3ic + ρ4id + ρ5ie) =Aa[ρ1ia + ρ2ib + ρ3ic + ρ4id + ρ5ie] +Bb[ρ1ia + ρ2ib + ρ3ic + ρ4id + ρ5ie] +Cc[ρ1ia + ρ2ib + ρ3ic + ρ4id + ρ5ie] +Dd[ρ1ia + ρ2ib + ρ3ic + ρ4id + ρ5ie] +Ee[ρ1ia + ρ2ib + ρ3ic + ρ4id + ρ5ie](3)
Aa[ρ1ia + ρ2ib + ρ3ic + ρ4id + ρ5ie] =Aρ1ia2 + Aaρ2ib + Aaρ3ic + Aaρ4id + Aaρ5ie(4) Since
a2 = -b + 2, ab = -a -c, ac= -b -d, ad=-c - e, ae=-d -eAρ1ia2 + Aaρ2ib + Aaρ3ic + Aaρ4id + Aaρ5ie =Aρ1i[-b + 2] + Aρ2i[-a -c] + Aρ3i[ -b -d] + Aρ4i[-c - e] + Aρ5i[-d -e](5) We can make the same type of argument for:
Bb[ρ1ia + ρ2ib + ρ3ic + ρ4id + ρ5ie] +Cc[ρ1ia + ρ2ib + ρ3ic + ρ4id + ρ5ie] +Dd[ρ1ia + ρ2ib + ρ3ic + ρ4id + ρ5ie] +Ee[ρ1ia + ρ2ib + ρ3ic + ρ4id + ρ5ie]so we are done.
QED
Theorem 3: The Eleventh Root of Unity is Solvable by RadicalsProof:
(1) Using Lemma 1
here, we have:
x10 + x9 + x8 + x7 + x6 + x5 + x4 + x3 + x2 + x + 1 = 0where
x is an eleventh root of unity and
x ≠ 1.
(2) Using Lemma 1
here and setting
y = -(x + x-1), we can simplify the equation to:
y5 - y4 -4y3 + 3y2 + 3y - 1 = 0(3) Using the fundamental theorem of algebra (see Theorem,
here), we know that there are
5 roots ot this equation which we can label:
a,b,c,d,e(4) The plan of attack for solving this equation is to use Vandermonde's equation (see Theorem,
here) to return
a,b,c,d,e as its answers.
(5) So for values:
a,b,c,d,e, we have:

where
Vi = (ρ1ia + ρ2ib + ρ3ic + ρ4id + ρ5ie) where each
ρk is a distinct 5th root of unity.
(6) Let
ω be a primitive a fifth root of unity. [See definition
here]
(7) Then, we can choose
ρk such that (see Theorem 3,
here):
ρ1 = 1, ρ2 = ω, ρ3 = ω3, ρ4 = ω2, and
ρ5 = ω4(8) So,
Vi(a,b,c,d,e) = a + ωib + ω2id + ω3ic + ω4ieand
Vi(b,d,e,c,a) = b + ωid + ω2ic + ω3ie + ω4ia(9) This then gives us that:
Vi(b,d,e,c,a) = ω-1Vi(a,b,c,d,e)(10) We can use the same logic to confirm that:
Vi(a,b,c,d,e)5 = Vi(b,d,e,c,a)5 = Vi(d,c,a,e,b)5 = Vi(c,e,b,a,d)5 =Vi(e,a,d,b,c)5since
(ωk)5 = (ω5)k = (1)k(11) Now, applying Lemma 2 above, we get:
Vi(a,b,c,d,e)5 = Aa + Bb + Cc + Dd + Ee + Fwhere
A,B,C,D,E,F are rational expressions in
ρ1, ..., ρ5(12) Reusing the same function in step #11 gives us:
Vi(b,d,e,c,a)5 = Ab + Bd + Ce + Dc + Ea + FVi(d,c,a,e,b)5 = Ad + Bc + Ca + De + Eb + FVi(c,e,b,a,d)5 = Ac + Be + Cb + Da + Ed + FVi(e,a,d,b,c)5 = Ae + Ba + Cd + Db + Ec + F(13) From step #10, step #11, and step #12, we have:
5Vi(a,b,c,d,e)5 = (A + B + C +D +E)(a + b + c + d +e) + 5F(14) Using Lemma 1 above, we know that
a + b + c + d + e =1, so we have:
5Vi(a,b,c,d,e)5 = (A + B + C +D +E) + 5Fwhich is the same as:
Vi(a,b,c,d,e)5 = 1/5(A + B + C + D +E) + F(15) Now, since
(a + b + c + d + e) = 1, we have as our solution:
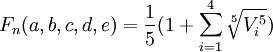
where
Vi(a,b,c,d,e)5 = 1/5(A + B + C + D + E) + Fand
A,B,C,D,E,F are functions of the fifth roots of unity which are expressible by radicals based on a previous result from de Moivre (see Theorem 1,
here)
QED
Here is the solution that Vandermonde came up with:
x = 1/5[1 + Δi + Δii + Δiii + Δiv]where:
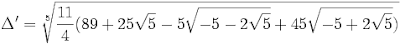
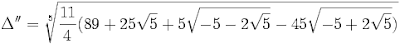
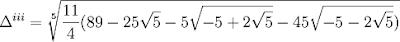
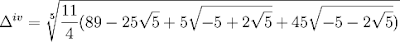
Please note that in Vandermonde's original work, there was a mistake. Professor Tignol sent me the corrections which I have updated above. This mistake was noticed by Oscar Luis Palacios-Velez.
References

















, World Scientific, 2001