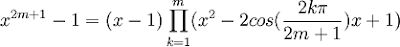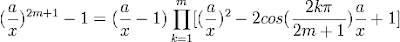In the case of n=2, this gives us: (x2 - 1)/(x - 1) = (x + 1). So, the other root of unity is x = -1.
In the case of n=3, this gives us: (x3 - 1)/(x - 1) = (x2 + x + 1). Using the quadratic equation to solve for this (see Theorem, here) gives us:
(-1 ± √1 - 4)/2 = (-1 ± √-3)/2.
In light of this and a previous result (see Lemma 1, here), it is possible to generate an equation to determine the primitive nth roots of unity.
Definition 1: Cyclotomic Polynomial Φn(x)
Φ1(x) = x - 1
Otherwise:

where d includes all divisors of n except for n itself.
Lemma 1:
If p is prime, then:
Φp = xp-1 + xp-2 + ... + x + 1
Proof:
(1) Since p is prime, the only divisor is 1 and:
Φp = (xp - 1)/(x - 1)
(2) Now, we know that (xp - 1)/(x - 1) = xp-1 + xp-2 + ... + x + 1 since:
(a) Let s = xp-1 + xp-2 + ... + x + 1
(b) x*s = xp + xp-1 + ... + x2 + x
(c) x*s - s = xp - 1
(d) s(x - 1) = xp - 1
(e) s = (xp - 1)/(x - 1)
QED
Now, the next thing we need is a proof that Φn will generate a polynomial whose solution is the primitive n-th roots of unity:
Theorem 2: Cyclotomic Polynomial
For every integer n ≥ 1, Φn is a monic polynomial (see Definition 5, here for monic if needed) with integral coefficients and:
Φn = ∏(x - ζ) ∈ Z[x]
where ζ runs over the set of primitive n-th roots of unity and Z is the set of integers.
Proof:
(1) For Φ1=x-1, the theorem is clearly true.
(2) Let's assume that the theorem is true up to n-1.
(3) Since d is always less than n, for each d, we have:
Φd(x) = ∏(x - ζ) ∈ Z[x]
where ζ runs over the roots of unity with exponent d.
(4) Since each root of Φd is a root of unity, it follows that Φd divides xn - 1 [see Lemma 1, here]
(5) If d1, d2 are distinct divisors of n, then it follows that Φd1 and Φd2 are relatively prime polynomials and distinct -- that is, they do not include any common root of unity since:
Each root of unity has a unique exponent so no root of unity included in Φn will be found in more than one divisor Φdi.
(6) Using Corollary 2.2, here, it follows that:

is a polynomial since it is divible by a product of all Φd
(7) Since each Φd is monic, it follows that Φn is monic.
(8) Since each Φd is in Z[x] and since xn - 1 is in Z[x], using the Division Algorithm for Polynomials, it follows that Φn is in Z[x]. [See Theorem, here]
(9) Now for each (x - ζi) that divides Φn, it follows that it's exponent equals n since:
(a) If its exponent is less than n and it is an n-th root of unity, then its exponent e is a divisor of n and it has been divided out.
(b) Assume that e doesn't divide n.
(c) So that n = qe + r where r ≥ 1 and r is less than e.
(d) Then:
(ζ)qe+r = 1 = (ζ)qe*(ζr)
(e) We know that (ζ)qe = 1 since:
(ζ)qe = (ζe)q
(f) But then:
ζr = 1/(ζqe) = 1
(g) This is impossible since r is less than e and e is the exponent of the root of unity.
(h) Therefore, we reject the assumption in 9b.
QED
References
- Jean-Pierre Tignol, Galois' Theory of Algebraic Equations
, World Scientific, 2001