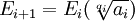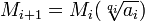Below is Pierre Lauren Wantzel's version of Ruffini's proof. Niels Abel independently presented his own version of this version which I covered previously.
Today's content is taken from Jean-Pierre Tignol's Galois' Theory of Algebraic Equations.
Lemma 1:
Let u,a be functions of n parameters in a field F such that up = a for some prime p.
Let n ≥ 5
Let σ be the following permutation:
x1 → x2 → x3 → x1 and xi → xi for i greater than 3.
so that:
σf(x1, x2, x3, ..., xn) = f(x2, x3, x1, ..., xn)
Let τ be the following permutation:
x3 → x4 → x5 → x3 and xi → xi for i=1,2 and i greater than 5
so that:
τf(x1, x2, x3, x4, x5, ..., xn) = f(x1, x2, x4, x5, x3, ..., xn)
Then:
If a is invariant under the permutations σ and τ, then so is u.
Proof:
(1) From the given, we have up = a where u,a are functions of n parameters.
(2) Applying the permutation σ to both sides gives us:
σ(u)p = σ(a)
(3) Since a is invariant with regard to σ, we have:
σ(u)p = σ(a)= a = up
(4) Dividing both sides by up gives us:
[σ(u)/u]p = 1
(5) Taking the p-th root of each side and multiplying by u gives us:
σ(u) = ζσu
where ζσ is some p-th root of unity.
(6) Applying σ to both sides gives us:
σ2(u) = ζσ2u
(7) Applying σ again we get:
σ3(u) = ζσ3u
(8) Now, we also know from its definition that σ3(u) = u since:
σ3f(x1, x2, x3, x4, ..., xn) = f(x1,x2, x3, x4, ..., xn)
(9) So, that ζσ3 = 1
(10) We can make the same line of argument with τ to show that:
τ(u) = ζτu
where ζτ is a pth root of unity and
ζτ3 = 1
(11) Putting these two results together gives us:
σ*τ(u) = σ(τ(u)) = ζσζτu
σ2*τ = σ2(τ(u)) = ζσ2ζτu
(12) Now, representing each of these as permutations we get:
σ*τ:
x1 → x2 → x3 → x4 → x5 → x1 and xi → xi for i greater than 5.
σ2*τ:
x1 → x3 → x4 → x5 → x2 → x1 and xi → xi for i greater than 5
(13) Using the above permutation maps, we get that:
(σ*τ)5(u) = u
(σ2τ)5(u) = u
(14) Using step #5 and step #10 above, we can use step #13 to conclude that:
(ζσζτ)5 = (ζσ2ζτ)5 = 1
(15) Now, we also note that:
ζσ = ζσ6*ζσ-5 = ( ζσ6*ζσ-5)*(ζτ5*ζτ-5)*(ζσ5*ζσ-5) = ζσ6*(ζτ5*ζσ5)*(ζσ-5*ζσ-5*ζτ-5) =
= ζσ6*(ζσζτ)5(ζσ2ζτ)-5
(16) But then using step #14 with step #15, we have:
ζσ = ζσ6*(ζσζτ)5[(ζσ2ζτ)5]-1 = ζσ6*(1)*(1)-1 = ζσ6
(17) Using step #9 above, we then have:
ζσ =(ζσ3)2 = (1)2 = 1
(18) Now, since (ζσζτ)5 =1, we have:
(1*ζτ)5 =1
so that:
ζτ5 = 1
(19) We can now show that ζτ = 1 since:
ζτ = ζτ6*ζτ-5 = (ζτ3)2*(ζτ5)-1
Taking ζτ3 = 1 (step #10) and ζτ5 = 1 (step #18), we get:
ζτ = (ζτ3)2*(ζτ5)-1 = (1)2*(1)-1 = 1
QED
Theorem 2: Ruffini's Theorem
Let P(X) = (X - x1)*...*(X - xn) = Xn - s1Xn-1 + ... + (-1)nsn = 0
where si are coefficients in field k.
Let K be a field such that K = k(s1, ..., sn)
If n ≥ 5 and F is a splitting field for P(X), then F/K is not a radical tower.
Proof:
(1) Since F is a splitting field for P(X), x1 ∈ F.
(2) Since K is defined around the coefficients of P, it is clear that all elements of K are invariant under the permutations of σ and τ. [See Lemma 2, here]
(3) Assume F/K is a tower of radicals such that:
K = F0 ⊂ F1 ⊂ ... ⊂ Fm-1 ⊂ Fm = F
such that for each 0 ≤ i ≤ m:

where pi is a prime and αi ∈ F0 = K
(4) Then, by induction, all elements Fi are also invariant against the permutations σ and τ since:
(a) We know that all elements of F0 = K are invariant under σ and τ (step #2 above) so we can assume that this is true up to some i where i ≥ 0.
(b) Let a = αi, u = a(1/p) so that:
Fi+1 = Fi(u)
and
a ∈ Fi
(c) But since a ∈ Fi, it follows that a is invariant under σ and τ.
(d) Using Lemma 1 above, we note that this implies that u is also invariant under σ and τ.
(e) But then all elements of Fi(u) = Fi+1 are also invariant under σ and τ.
(5) But now we have a contradiction since x1 ∈ F = Fm is not invariant under σ [since σ(x1) = x2]
(6) So, we reject our assumption in step #3.
QED
References
- Michael I. Rosen, "Niels Hendrik Abel and Equations of the Fifth Degree", The American Mathematical Monthly, Vol. 102, No. 6 (Jun. - Jul., 1995), pp 495-595.
- Jean-Pierre Tignol, Galois' Theory of Algebraic Equations
, World Scientific, 2001
- Jorg Bewersdorff, Galois Theory for Beginners
, American Mathematical Society, 2006.