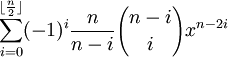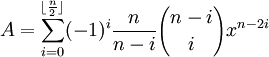2cos(nα) = Fn(2cosα) where n ≥ 1.
and
2sin(nα) = (-1)(n-1)/2Fn(2sinα) where n is odd and n ≥ 1.
Here are the details:
Lemma 1: n ≥ 1 → 2 cos(n)α = (2cos α)(2 cos (n-1)α) - 2 cos(n-1)α
Proof:
(1) From the addition and subtraction cosine formulas [see Theorem 1, here], we know that:
cos (a + b) = cos a cos b + sin a sin b
cos (a - b) = cos a cos b - sin a sin b
(2) Adding these two identities together gives us:
cos (a + b) + cos (a - b) = cos a cos b + cos a cos b = 2cos a cos b
Or in other words:
cos (a + b) = 2 cos a cos b - cos (a - b)
(3) Since a,b can be any value, let b = α, let a = (n-1)α
So that:
a + b = (n-1)b + b = (n-1+1)b = nα
a - b = (n-1)b - b = (n-2)α
(4) This then gives us that:
cos (nα) = (cos α)(2 cos(n-1)α) - cos(n-2)α
Or equivalently:
2 cos (nα) = (2 cos α)(2 cos(n-1)α) - 2 cos(n-2)α
QED
This trigonometric identity is relevant to Van Roomen's problem because it fits the same structure as Fn
In my previous blog, I showed that Fn(x) = x*Fn-1(x) - Fn-2(x).
Now, if x = 2 cos α, then we have:
Fn(2 cos α) = (2 cos α)*Fn-1(2 cos α) - Fn-2(2 cos α)
This brings us to the corollary:
Corollary 1.1: 2 cos(nα) = Fn(2 cos α)
Proof:
(1) At n = 1:
F1 = x = 2 cos α = 2 cos(n α)
(2) At n = 2:
F2 = x2 - 2 = (2 cos α)2 - 2 = 2(2 cos2(α) - 1)
Since sin2(x) + cos2(x) = 1 (see Corollary 2, here), we have :
2(2 cos2(α) - 1) = 2(2 cos2(α) - [sin2(α) + cos2(α)] ) = 2[cos2(α) - sin2(α)]
Using the formula for cos(2x) (see Lemma 3, here), we get:
2[cos2(α) - sin2(α)] = 2 (cos 2 α)
(3) So, let's assume that Fn(2 cos α) = 2 cos n α up to n-1 where n ≥ 3.
(4) Now, using our previous formula (see Theorem 1, here), we know that:
Fn(x) = x*Fn-1(x) - Fn-2(x)
(5) Using our assumption in step #3, we have:
Fn(2 cos α) = (2 cos α)*(2 cos(n-1)α) - (2 cos(n-2)α)
(6) Now, using Lemma 1 above, we know that:
2 cos nα = (2 cos α)*(2 cos (n-1)α) - (2 cos(n-2)α) so that by induction (see Theorem, here for review if needed), we have proven that:
Fn(2 cos α) = 2 cos n α
QED
But we are not yet done, we can also show:
Corollary 1.2: For all odd n ≥ 1:
2 sin nα = (-1)(n-1)/2Fn(2 sin α)
Proof:
(1) From a previous result (see Lemma 1, here), we know that:
cos(z) = sin(z + π/2) where z is any number in radians (see here for review of radians).
(2) Let z = x - π/2
(3) Then:
cos(x - π/2) = sin(x - π/2 + π2) = sin(x)
(4) Now from Corollary 1.1 above, we have:
2 cos(nα) = Fn(2 cos α)
(5) Since α can be any value let α = β - π/2
so that:
2 cos(n[β - π/2]) = 2 cos(nβ - nπ/2) = 2 cos([nβ - (n-1)π/2] - π/2) = 2 sin(nβ - (n-1)π/2)
and
Fn(2 cos (β - π/2)) = Fn(2sin(β))
(6) Using the formula for sin(a+b) [see Theorem 1, here], we get:
sin(nβ - (n-1)π/2) = sin(nβ)cos([n-1]π/2) - cos(nβ)sin([n-1]π/2)
(7) Since n is odd, we know that n-1 is even and there exists m such that (n-1)=2m which gives us:
cos([n-1]π/2) = cos(mπ) = (-1)m since:
(a) n ≥ 1 so m ≥ 0.
(b) cos(0) = 1, cos(π)= -1 [See Property 6, here]
(c) Finally cos(x + 2π) = x [See Property 5, here]
(d) If m is even, then mπ is divisible by 2π and cos(mπ) = 1 = (-1)m
(e) If m is odd, then mπ is not divisible by 2π and cos(mπ) = -1 = (-1)m
Likewise:
sin([n-1]π/2) = sin(mπ) = 0 since:
(a) n ≥ 1 so m ≥ 0.
(b) sin(0) = 0, sin(π) = 0 [see Property 1, here]
(c) sin(x + 2π) = sin x [See Property 5, here]
(d) Putting this together, we can see that mπ ≡ 0 or ≡ π (mod 2π) and either way sin(mπ)=0.
(8) So that we have:
2 sin(nβ - (n-1)π/2) = 2*[sin(nβ)cos([n-1]π/2) - cos(nβ)sin([n-1]π/2)] = 2*(-1)(n-1)/2*sin(nβ) - cos(nβ)*0 = 2*(-1)(n-1)/2sin(nβ)
(9) Using step #8 and combining it with step #4 and step #5 gives:
2*(-1)(n-1)/2sin(nβ) = Fn(2sin(β))
(10) Multiplying both sides by (-1)(n-1)/2 gives us:
2sin(nβ) = (-1)(n-1)/2Fn(2sin(β))
QED
References
- "Cos of multiples of x, in terms of cos x ", MathHelp
- Jean-Pierre Tignol, Galois' Theory of Algebraic Equations
, World Scientific, 2001