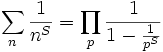Today's blog continues the discussion on
Ernst Kummer's Theory of Ideal Numbers and his proof of
Fermat's Last Theorem for Regular Primes. For historical context, start
here.
Today's content is taken straight from Harold M. Edwards
Fermat's Last Theorem: A Genetic Introduction to Algebraic Number Theory.
For standard integers, when we have:
uv = wλIf
gcd(u,v)=1, then we know that
u,v are both
λth powers. (see Theorem,
here)
When it comes to
cyclotomic integers, unfortunately, this proof does not hold because to use unique factorization, we have to go through ideal numbers. Today's blog is about the method used by Kummer to apply this reasoning to ideal numbers.
For example, we know that if
U is a
principal divisor for
u and
V is a principal divisor for
v, and
gcd(U,V)=I, then
U,V are
λth; powers. That is, there exists
C,D such that:
U = Cλ, V = Dλ where
C,D are ideal numbers.
Lemma 1: gcd(U,V)=I and u(α)v(α)=w(α)n, then there exists C,D such that U=Cn, V=DnProof:
(1) So, we start with
gcd(U,V) = I, UV = Wn [We know this since principal divisors have the same relations as their corresponding cyclotomic integers, see here]
(2) Assume that
U is not equal to any ideal number
Xn
(3)
U ≠ I since
I is an
Xn power [Since
In = I]
(4) Now,
U is divisible by a prime divisor
P. [See Definition 3,
here]
(5) So, there exists
K such that
U = PK
(6)
P divides
W since
Wn = UV = PKV [By applying
Euclid's Lemma for Prime Divisors]
(7) So, there exists
M such that
W=PM
(8) So,
Wn = UV = PKV = (PM)n = PnMn
(9) Dividing
P from both sides gives us:
KV = P(n-1)Mn
(10) From Euclid's Lemma,
P divides
K or
V.
(11) It can't divide
V since it already divides
U and
gcd(U,V)=I. Therefore, it divides
K
(12) We can apply this same argument for each
P in
P(n-1)
(13) So, we can conclude that
P(n-1) divides
K.
(14) So, there exists
Z such that
K = p(n-1)*Z
(15) So,
KV = P(n-1)Mn = P(n-1)*Z*V
(16) Dividing
p(n-1) from both sides gives us:
ZV = Mn
(17) Now,
gcd(Z,V)=1 since
Z is a divisor of
U and
gcd(U,V) = I
(18) Likewise,
Z cannot be an n-power. If it were, then
U = pnZ would make
U an n-power which goes against our assumption in step #2.
(19) Finally,
N(Z) is less than
N(U) since
N(P(n-1)) > 1.
(20) Thus, we have a contradiction by infinite descent.
QED
In order to prove that
u,v are both
λth powers we need to show that
C,D are principal.
This then is the problem that Kummer addressed, under what circumstances can we assume that
U = Cλ where
U is principal imply that
C is also principal.
To help with this question, let's consider an important insight.
Theorem 2: For any ideal number C, if h is the class number, then Ch ~ IIn other words,
Ch is principal.
Proof:
(1) Let
h be the
class number for the cyclotomic integers corresponding to
λ(2) Based on the theorem regarding class numbers (see Theorem,
here), we know that all ideal numbers are equivalent to one of the ideal numbers of a representative set:
A1, A2, ..., Ah(3) This means that each of the ideal numbers
C, C2, C3, etc. are equivalent to an ideal number
Ai(4) Since there are only
h such ideal numbers in the representative set, eventually, there are two ideal numbers
Cj and
Cj+k that are equivalent to the same
Ai and therefore equivalent to each other.
(5) For each ideal number, there exists another ideal number
B such that:
CjB is principal [See Lemma 6,
here]
(6) Because
Cj ~ Cj+k:
Cj+kB is also principal.
(7) But
Cj+kB is principal and
CjB is principal, then
Ck is also principal. (See Lemma 2,
here)
(8) Let
d be the first power of
C that is principal.
So that we have:
Cd ~ IC, C2, ..., Cd-1 are inequivalent to each other and not principal.
If any of these were equivalent to each other, then there would a power less than
d which is principal which goes against our definition of
d.
(9) Since
I,C, C2, ..., Cd-1 are all inequivalent, then we know that they correspond to
d of the
Ai which make up the representative set of ideal numbers.
(10) If this exhausts all the elements of the represenative set then
d=h so to complete this proof, we only need to consider the situation where
d is less than
h.
(11) If
d is less than
h, then there is an ideal number
Ai that is not equivalent to any of the powers
I,C,C2, ..., Cd-1. Let's call it
E.
(12) Then
E, EC, EC2, ..., ECd-1 give
d more ideal numbers that are inequivalent to each other and inequivalent to the first set of
d ideal numbers (in step #11).
(a) Assume
ECi ~ ECj where
i ≠ j and both
i,j are positive integers less than
d.
(b) So that we have
ECi ~ ECi+k where
i+k=j.
(c) Then we have a
Ck that is principal where
k is less than
d which is impossible so we reject our assumption.
(d) Assume
E ~ ECi where
i is less than
d.
(e) Then we have
Ci is principal which again is impossible.
(f) Assume
ECi ~ Cj(g) If
j ≥ i, then this gives us that
E is principal which goes against our assumption step #11 so we can reject this.
(h) If
j is less than
i, then we have:
ECj+k ~ CjThis gives us that
Cj is principal which goes against our assumption since
j is less than
d.
(i) So, steps (a) thru (h) prove that this new set
E, EC, EC2, ..., ECd-1 is inequivalent to each other and to the powers of
Ci.
(13) This either exhausts all
Ai of the representative set or we can do the same thing until we are done. At the end, we are left with a disjoint set of
d elements each.
(14) This gives us that
d divides
h so that
Cd ~ I → Ch ~ I.
QED
Using the Theorem above, it is now possible to state under what conditions
Cλ is principal implies that
C is principal.
Corollary 2.1: If Cλ ~ I and λ doesn't divide the class number h, then C ~ IProof:
(1) Because
λ is prime, if
h is not divisible by
λ, then there exists
m,n such that
mh = nλ + 1. [See Lemma 1,
here for proof]
(2)
I ~ Ch (from Theorem 1 above) so
I ~ (Ch)m (see Lemma 1,
here)
(3)
(Ch)m = Chm = Cnλ+1 = (Cλ)nC(4) From the given we know that
(Cλ) ~ I so we also know that
(Cλ)n ~ I.
(5) But
I*C = C so
(Cλ)nC ~ I*C ~ C(6) Since
I ~ (Cnλ+1) and (Cnλ+1)~C, it follows that
C ~ I and therefore, that
C is principal.
QED
So, the corollary gives us the justification for considering the situation where
λ doesn't divide the class number. This is Kummer's
condition (A).
(A) The exponent
λ has the property that it does not divide the corresponding class number.
Let's return now to the original problem. Let's say we have:
uv = wλwhere
gcd(u,v)=1 and
λ does not divide the corresponding class number.
In this case we have that there exists
C,D such that
Cλ = U, Dλ=V and both
C,D are principal.
This gives us that there exists cyclotomic integers
c,d such that:
u = ecλv = e'dλwhere
e,e' are cyclotomic units.
This did not satisfy Kummer. He wanted to find the condition where we could conclude that:
u = cλv = dλThis leads us to
condition (B)(B) The exponent
λ should have the property that a unit
e in the set of corresponding cyclotomic integers has the following property:
e ≡ integer (mod λ) if and only if there exists a unit
e' such that
e = (e')λTo show the value of this. let's consider a second theorem.
Lemma 3: (a0 + a1 + ... + aλ-1)λ ≡ a0λ + a1λ + ... + aλ-1λ (mod λ)(1)
(a + b)λ ≡ aλ + bλ (mod λ) (See Lemma 1,
here)
(2)
(a + c + d)λ ≡ (a + (c+d))λ ≡ aλ + (c+d)λ (mod λ)(3) Since
(c + d)λ ≡ cλ + dλ (mod λ)(4) So that we have
(a + c + d)λ ≡ aλ + (c+d)λ ≡ aλ + cλ + dλ ≡ (mod λ)(5) Using the same logic we can show that:
(a + b + c + d + ...)λ = (a + (b + (c + (d + ...)))λ ≡ aλ + bλ + cλ + ... (mod λ)QED
Corollary 3.1: if g(α) is a cyclotomic integer then g(α)λ ≡ integer (mod λ)Proof:
(1) Because
g(α) is a cyclotomic integer, we have:
g(α) = a0 + a1α + ... + aλ-1αλ-1 [See Lemma 1,
here]
(g(α))λ = (a0 + a1α + ... + aλ-1αλ-1)λ ≡ (a0)λ + (a1α)λ + ... + (aλ-1αλ-1)λ (mod λ) [See Lemma 3 above]
(2) Since
(αi)λ = (αλ)i = 1i = 1, we have:
(g(α))λ ≡ (a0)λ + (a1)λ + ... + (aλ-1)λ (mod λ) = integerQED
Theorem 4: if a set of cyclotomic integers corresponding to an odd prime λ satisfies condition (A) and condition (B) and u ≡ integer (mod λ), then if uv=wλ where gcd(u,v)=1, then u,v are λth powers.Proof:
(1) From Corollary 2.1 above, we have:
u = ecλ(2)
u ≡ ecλ ≡ e*b (mod λ) for some integer b [See Corollary 3.1 above]
(3) So
e ≡ integer (mod λ) since
e ≡ u/b (mod λ) where
b divides
u and both
b,u are congruent to integers
mod (λ).(4) So therefore (condition B), there exists
e' such that
e = (e')λ(5) Let
c' = (e'c)(6) Then we have:
u= (c')λ We can make the same argument for
v so we are done.
QED
Definition 1: Regular PrimeA prime
λ is a
regular prime if
λ and the corresponding cyclotomic integers satisfy the following two conditions:
(A) The exponent
λ has the property that it does not divide the corresponding class number.
(B) The exponent
λ should have the property that a unit
e in the set of corresponding cyclotomic integers has the following property:
e ≡ integer (mod λ) if and only if there exists a unit
e' such that
e = (e')λWe can now use this definion to establish the following theorem:
Lemma 5: For a regular prime λ, if a corresponding cyclotomic integer g(α) has a divisor G which is a λth power and g(α) ≡ integer (mod λ), then there exists a cyclotomic integer h(α) such that g(α) = h(α)λProof:
(1) Since
G is
λth power, there exists a divisor
H such that:
G = Hλ(2) Since
λ is regular (see Definition 1 above), we know that
H is principal (see Corollary 1.1 above)
(3) Therefore, there exists
h(α) such that
H is the principal divisor for
h(α) (see Definition 2,
here for definition of a principal divisor)
(4) So we have
g(α) = eh(α)λ where
e is a unit.
(5) Now,
g(α) ≡ integer (mod λ) [from the given]
(6) Further,
h(α)λ ≡ integer (mod λ) [from Corollary 3.1 above]
(7) So, from this, we have:
e ≡ integer/integer ≡ integer (mod λ) [since
h(α) divides
g(α) and both are congruent to integers mod (λ)
(8) So by Condition (B), there exists
e' such that
e = (e')λ(9) Let
h'(α) = e'h(α)(10) Then we have that
g(α) = (h'(α))λQED
Theorem 6: Criteria for a λth powerif
g(α) ≡ nonzero (mod λ), then
g(α) = h(α)λ if and only if its divisor is a
λth power and
g(α) ≡ integer (mod λ)if
g(α) ≡ 0 (mod λ), then
g(α) = h(α)λ if and only if its divisor is a
λth power and its quotient by the largest power of
α - 1 is congruent
mod λ to an integer.
Proof:
Case I: g(α) = h(α)λ → ∃ G,H such that
G = Hλ and
g(α) ≡ integer (mod λ)(1) Assume
g(α) ≡ nonzero (mod λ)(2) Assume
g(α) = h(α)λ(3) Let
G,H be divisors of
g(α),h(α)(4) We can see that
G = Hλ so
G is a
λth power [See Theorem,
here]
(5) We can also see that
g(α) ≡ integer (mod λ) since
h(α)λ ≡ integer (mod λ) from Corollary 3. 1 above.
QED
Case II: G = Hλ and
g(α) ≡ integer (mod λ) → ∃ h(α) such that
g(α)=h(α)λ(1) This follows from Lemma 5 above.
QED
Case III: g(α) ≡ 0 (mod λ), g(α) = h(α)λ → an ideal number
G is a
λth power and quotient by the largest power of
α - 1 is congruent mod
λ to an integer
(1) Assume
g(α) = h(α)λ(2) Let
G,H be the divisor of
g(α),h(α)(3)
G = Hλ so we that its divisor
G is a
λth power. [See Theorem,
here]
(4) Since
g(α) is divisible by
λ, it is divisible by
(α-1) since
(α-1)λ-1 = λ (see Corollary 3.2,
here) so that we have:
g(α) = (α-1)kg'(α) where
g'(α) is not divisible by
(α - 1) and
k ≥ 1.
(5) Since
α - 1 is a prime divisor and since
g(α) is a
λth power,
λ must divide
k so that we have:
g(α) = [(α-1)k/λ]λg'(α)(6) By the same argument, the powers of the prime divisors that divide
g'(α) must also be divisible by
λ so that there exists an ideal number
H' such that:
G' = (H')λ(7) Since
G' = (H')λ is principal, then
H' must also be principal so that there exists
h'(α) such that:
g'(α) = eh'(α)λ where
e is a unit.
But since
h(α)λ = [(α-1)k/λ]λg'(α), it follows that
e must also be a
λth power.
(8) But the only way this is possible by Condition B is if
e ≡ integer (mod λ)(9) Therefore, we have
g(α) ≡ e * h(α)λ ≡ integer * integer (mod λ)QED
Case IV: if its divisor
G is a
λth power and its quotient by the largest power of
α - 1 is congruent mod
λ to an integer →
g(α)=h(α)λ(1) So there exists an ideal number
H such that
G = Hλ(2)
g(α) = (α-1)k*g'(α)(3) So
g'(α) ≡ integer (mod λ)(4)
H is principal from Corollary 2.1 above so there exists
h(α) such that
g(α) = eh(α)λ(5) Let
G' be the principal divisor for
g'(α)(6) Since
G is a
λth power, all the powers of the prime divisors that make up
G must be divisible by
λ.
(7) If
G' is all the prime divisors minus
(α - 1),
G' must also be a
λth power so that there exists
H' such that
G' = (H')λ(6) Since
G' = (H')λ is principal,
H' is principal (See Corollary 2.1 above)
(7) So there exists
h'(α) such that
g'(α) ≡ eh'(α)λ(8) Now
g'(α) ≡ integer (mod λ) [from given] and
h'(α)λ ≡ integer (mod λ) [from Corollary 3.1 above) so that
e ≡ integer (mod λ)(9) Now using Condition B, this gives us that there exists
e' such that
e = e'λ(10) This then gives us that
g'(α) = [e'h'(α)]λ(11) This also gives us that
g(α) = [(α-1)k/λe'h'(α)]λQED
Kummer made three conjectures regarding regular primes:
(1) There exist irregular primes that do not satisfy conditions (A) and (B). [Proof that
37 is irregular will be proved later]
(2) Condition (A) implies Condition (B). [Proof of this will be presented later]
(3) Regular primes are infinite in number.
This last conjecture is still an open question. There has a been proof that there are infinite irregular primes but no one has proven that there are infinite regular primes. Kummer was able to prove the first two conjectures within a few months after the stated them. The third conjecture he later retracted saying that he didn't know.