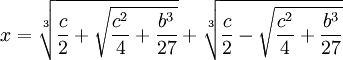The content in today's blog is taken from Jean-Pierre Tignol's Galois' Theory of Algebraic Equations.
(1) Ferrari started out with a quadratic equation of the following form:
x4 + bx3 + cx2 + dx + e = 0
(2) Then, he borrowed a method from Girolamo Cardano (see here) and set y = x + (b/4) which means x = y - (b/4).
(3) Substituting x = y - (b/4) gives us:
(y - [b/4])4 + b(y - [b/4])3 + c(y - [b/4])2 + d(y - [b/4]]) + e = 0
Working this through (see details here), gives us:
y4 + py2 + qy + r = 0
where:
p = c - 6(b/4)2
q = d - (b/2)c + (b/2)3
r = e - (b/4)c + (b/4)2c - 3(b/4)4
(4) Now if we move the q and r term over we get:
y4 + py2 = -qy -r
This helps us because if we add (p/2)2 to both sides, we can complete the square to get:
(y2 + p/2)2 = -qy -r + (p/2)2
(5) Now, if we add a value u to our square, we get the following:
(y2 + p/2 + u)2 = -qy -r + (p/2)2 + 2uy2 + pu + u2
This may not appear to help us but it gives us a possibility for completing the square on the other side.
(6) For example, if we could find a value u such that:
-qy -r + (p/2)2 + 2uy2 + pu + u2 = ([√2uy - q/(2√2u)]2
Then we have found a solution (see step #11 if this point is not clear)
(7) Now:
([√2uy - q/(2√2u)]2 = 2u2y2 - 2*(√2uy)(q/(2√2u)) + q2/(8u) =
= 2u2y2 - q/u + q2/(8u)
(8) So this equation works only if:
-qy -r + (p/2)2 + 2uy2 + pu + u2 = 2uy2 - qy + q2/(8u)
That is if:
-r + (p/2)2 + pu + u2 = q2/(8u)
(9) But if we multiply 8u to all sides and then subtract by q2, we get:
8u3 + 8pu2 + (2p2 - 8r)u - q2 = 0
(10) This is the general cubic equation which we can solve using Cardano's formula so we know that u can take on this value.
(11) This then gives us:
(y2 + p/2 + u)2 = ([√2uy - q/(2√2u)]2.
(12) This can we solve using the quadratic equation. The four solutions can be found from:
(y2 + p/2 + u)2 = ± [√2uy - q/(2√2u)]
I should probably note that we assumed that u ≠ 0. I will talk about the situation were u = 0 in my next blog where I provide a proof for Ferrari's solution.
References
- Jean-Pierre Tignol, Galois' Theory of Algebraic Equations
, World Scientific, 2002