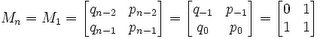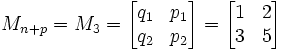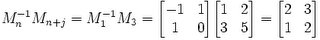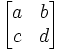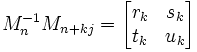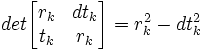Today's blog is a continuation of the discussion about the famous math problem known as
Pell's Equation.
In today's blog, I will show proofs for two properties of
Continued Fractions (for those not familiar with Continued Fractions, start
here):
- All rational numbers can be represented as a finite continued fraction.
- All irrational numbers that are solutions to a quadratic equation are periodic (that is, they repeat the same pattern of integers over and over again after a certain point)
For the irrational numbers, I mean any irrational number that is a solution to a quadratic equation that is of this form:
ax2 + bx + c = 0where a,b,c are integers.
For a periodic continued fraction which a period of size j and where the period begins before
i, then: a
i = ai+j.
The proofs outlined in today's blog are based on work done by Harold M. Stark in his book
An Introduction to Number Theory.
Theorem 1: A continued fraction is finite if and only if it is a rational number.(1) We know that if a continued fraction is finite, then it is representable as a rational number. (See Lemma 2,
here)
(2) So, all we need to prove is that a rational number is representable as a finite continued fraction.
(3) For any rational number, there are two integers, let's call them
c,d0 such that the rational number is representable by
a/b. [Definition of a
rational number]
(4) To generate a continued fraction, we need to generate a set of integers
a0 through
an.
(5) Let's set
a0 = floor(c/d0).
A floor is a function that returns the minium integer that is less than or equal to a certain rational value. For example, the
floor of
(3/4) is
0. The
floor of
(5/2) is
2 and the
floor of
(-8) is
-8. Finally, the
floor of
(-8.1) is
-9.
(6) If
a0 = c/d0, then we are done and the continued fraction is
[a0]. Going forward, we will assume that
a0 is less than but not equal to
c/d0.
(7) Subtracting the original number by the
a0 results in a rational number which we can call
β0:
c/d0 = a0 + β0We note that
β0 is
≥ 0 and less than
1 by our assumption in #6. When it is
0 we are done.
(8) Now, from #7, we know that
d0 * β0 is an integer since:
c = d0 * a0 + d0*β0And therefore:
d0 * β0 = c - d0*a0Which is an integer since
c is an integer and
d0 is an integer and
a0 is an integer.
(9) So, we know there exists an integer
d1 = d0 * β0.
We also note that this integer has the following properties:
(a)
d1 ≥ 0.
We know that it is not negative since we can assume
d0 is positive (if both
c,d0 are negative, we can assume that they are both positive. If
c is positive and
d0 is negative, we can assume that
c is negative and
d0 is positive.
(b)
d1 is less than
d0We know it is less than
d0 since
β0 is less than
1 and since
d1 = d0 * β0(10) From #9, we note that
β0 = d1/d0(11) Now,
a1 = floor(1/β0) = floor(d1/d0)Now if this is an integer (for example,
1/(1/2) = 2), then we are done and the continued fraction is
[a0,a1]. So, let's assume that we are not done.
(12) So, then, there exists rational value
β1 that is equal to the difference between
1/β0 and
a1 which is greater than
0 so that:
d1/d0 = a1 + β1This is the same form as step #7 and the same principles apply. We can derive a
d2 that is a positive integer less than
d1 and so on.
(13) Because
di is an integer that continually gets smaller, we know that eventually it will equal
0.
(14) When
di = 0 we are done and so we have proven that our sequence will eventually end.
QED
Lemma 1: If a continued fraction is periodic, then it represents a quadratic number.(1) A quadratic number is any real number that satisfies the quadratic equation:
ax2 + bx + c = 0 where
a,b,c are integers.
For example,
√2 is a quadratic number since it satisfies the equation
(a=1,b=0,c=-2) where:
x2 - 2 = 0(2) Let
α be a real number that is represented by a periodic continued fraction that repeats a
am with a period of
k.
So
α = [ a0, a1, ..., am-1, αm]And
αm = [ am, am+1, ..., am+k-1, am, am+1, ...]And
αm = [ am, am+1, ..., am+k-1, αm](3) So, applying Lemma 1 from a
previous blog, we get:
αm = (αmpm + pm-1)/(αmqm + qm-1)(4) And multiplying
(αmqm + qm-1) to both sides gives us:
(αm)2*qm + αm*qm-1 = (αmpm + pm-1)And:
(αm)2*qm + αm*qm-1 - αmpm - pm-1 = 0And:
(αm)2*qm + (αm)(qm-1 - pm) - pm-1= 0(5) Applying lemma 1 from a
previous blog to the first equation in #2 gives us:
α = (αm*pm-1 + pm-2)/(αm*qm-1 + qm-2)(6) So,
α*(αm*qm-1 + qm-2) = (αm*pm-1 + pm-2)and
α*αm*qm-1 + α*qm-2 - αm*pm-1 - pm-2 = 0and
αm(α*qm-1 - pm-1) = pm-2 - α*qm-2and
αm = (pm-2 - α*qm-2)/(α*qm-1 - pm-1)(7) Now inserting (#6) into (#4) gives us:
[ ([pm-2 - α*qm-2)/(α*qm-1 - pm-1)]2*qm +[(pm-2 - α*qm-2)/(α*qm-1 - pm-1)](qm-1 - pm) - pm-1 = 0And multiplying
(α*qm-1 - pm-1)2 to both sides give us:
(pm-2 - α*qm-2)2*qm +(pm-2 - α*qm-2)(α*qm-1 - pm-1)(qm-1 - pm) - (α*qm-1 - pm-1)2(pm-1) = 0(8) And solving for all the values above gives us a quadratic equation of the form:
α2a + αb + c = 0QED
Lemma 2: If α is a quadratic number, and [a0, a1, ... , an-1, αn] is a continued fraction representation where ai are integers and αn is a real number, then αn is also a quadratic number.(1) Since
α is a quadratic number, there exists integers
a,b, and
c such that:
a(α)2 + b(α) + c = 0. [Definition of a quadratic number]
(2) From Lemma 1 in a
previous blog, we know that:
α = (αn * pn-1 + pn-2)/(αn* qn-1 + qn-2)(3) Inserting (1) into (2) and then multiplying everything out and then regrouping around
(αn)2, αn, and any integer gives us three values
An, Bn, Cn such that:
An(αn)2 + Bn(αn) + Cn = 0.
where
An = a(pn-1)2 + bpn-1qn-1 + c(qn-1)2Bn = 2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2Cn = a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 = An-1(4) By definition, this means that
αn is a quadratic number.
QED
Corollary 2.1: (Bn)2 - 4AnCn = b2 - 4acwhere:
An = a(pn-1)2 + bpn-1qn-1 + c(qn-1)2Bn = 2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2Cn = a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 = An-1(1) From Lemma 2 above:
(Bn)2 - 4AnCn =
= (2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) - 4*[a(pn-1)2 + bpn-1qn-1 + c(qn-1)2][a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 = An-1] =
= (2apn-1pn-2 )(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) +
(bpn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) +
(bpn-2qn-1)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) +
(2cqn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) -
(4a(pn-1)2)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] -
(4bpn-1qn-1)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] -
(4c(qn-1)2)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ]
(2) Multipyling each term, we get:
(i)
(2apn-1pn-2 )(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) =
4a2(pn-1)2(pn-2)2 + 2ab(pn-1)2(pn-2)(qn-2) + 2ab(pn-1)(pn-2)2(qn-1) + 4ac(pn-1)(pn-2)(qn-1)(qn-2)
(ii)
(bpn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) =
2ab(pn-1)2(pn-2)(qn-2) +
b2(pn-1)2(qn-2)2 +
b2(pn-1)(pn-2)(qn-1)(qn-2) +
2bc(pn-1)(qn-1)(qn-2)2
(iii)
(bpn-2qn-1)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) =
2ab(pn-1)(pn-2)2(qn-1) +
b2(pn-1)(pn-2)(qn-1)(qn-2) +
b2(pn-2)2(qn-1)2 +
2bc(pn-2)(qn-1)2(qn-2)
(iv)
(2cqn-1qn-2)(2apn-1pn-2 + bpn-1qn-2 + bpn-2qn-1 + 2cqn-1qn-2) =
4ac(pn-1)(pn-2)(qn-1)(qn-2) +
2bc(pn-1)(qn-1)(qn-2)2 +
2bc(pn-2)(qn-1)2(qn-2) +
4c2(qn-1)2(qn-2)2
(v)
-(4a(pn-1)2)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] =
-4a2(pn-1)2(pn-2)2 + -4ab(pn-1)2(pn-2)(qn-2) + -4ac(pn-1)2(qn-2)2
(vi)
-(4bpn-1qn-1)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] =
-4ab(pn-1)(pn-2)2(qn-1) +
-4b2(pn-1)(pn-2)(qn-1)(qn-2) +
-4bc(pn-1)(qn-1)(qn-2)2
(vii)
-(4c(qn-1)2)[a(pn-2)2 + bpn-2qn-2 + c(qn-2)2 ] =
-4ac(pn-2)2(qn-1)2 +
-4bc(pn-2)(qn-1)2(qn-2) +
-4c2(qn-1)2(qn-2)2
(3) We can see that many of these terms line up and cancel out:
=
[ 4a2(pn-1)2(pn-2)2 - 4a2(pn-1)2(pn-2)2 ]+ { from 2.i and 2.v }
[ 2ab(pn-1)2pn-2qn-2 + 2ab(pn-1)2pn-2qn-2 - 4ab(pn-1)2pn-2qn-2 ] + { from 2.i, 2.ii, and 2.iv }
[ 2ab(pn-1)(pn-2)2(qn-1) + 2ab(pn-1)(pn-2)2(qn-1) - 4ab(pn-1)(pn-2)2(qn-1) ]+ { from 2.i, 2.iii, and 2.vi }
[ 2bcpn-1(qn-1)2qn-2 + 2bcpn-1(qn-1)2qn-2 - 4bcpn-1(qn-1)2qn-2 ] + { from 2.iii, 2.iv, and 2.vii }
[ 2bcpn-2qn-1(qn-2)2 +2bcpn-2qn-1(qn-2)2 - 4bcpn-2qn-1(qn-2)2 ] + { from 2.ii, 2.iv, and 2.vi }
( 4c2(qn-1)2(qn-2)2 - 4c2(qn-1)2(qn-2)2 ) + { from 2.iv and 2.vii }
( b2pn-1pn-2qn-1qn-2 + b2pn-1pn-2qn-1qn-2 - 4b2pn-1pn-2qn-1qn-2 ) + { from 2.ii, 2.iii, and 2.vi }
(4acpn-1pn-2qn-1qn-2 + 4acpn-1pn-2qn-1qn-2)
+ { from 2.i and 2.iv }
[b2(pn-1)2(qn-2)2 + b2(pn-2)2(qn-1)2 ] + { from 2.ii and 2.iii }
[-4ac(pn-2)2(qn-1)2 +-4ac(pn-1)2(qn-2)2 ] { from 2.v and 2.vii }
= -2b2pn-1pn-2qn-1qn-2 + 8acpn-1pn-2qn-1qn-2 +b2(pn-1)2(qn-2)2 +b2(pn-2)2(qn-1)2 +-4ac(pn-2)2(qn-1)2 +-4ac(pn-1)2(qn-2)2 == b2[(pn-1)2(qn-2)2 + (pn-2)2(qn-1)2 - 2pn-1pn-2qn-1qn-2] - 4ac[(pn-1)2(qn-2)2 + (pn-2)2(qn-1)2 - 2pn-1pn-2qn-1qn-2] == (b2 - 4ac)[(pn-1)2(qn-2)2 + (pn-2)2(qn-1)2 - 2pn-1pn-2qn-1qn-2] == (b2 - 4ac)(pn-1qn-2 - pn-2qn-1)2(4) Applying Lemma 2 from a
previous blog, we get:
(b2 - 4ac)(pn-1qn-2 - pn-2qn-1)2= (b2 - 4ac)(-1)2 == b2 - 4ac.QED
Corollary 2.2: An, Bn, Cn can only span over a finite set of integers.(1) Let
λn = pnqn - α(qn)2(2) Rearranging values gives us:
pn = λn/qn - αqn(3) We note that
absolute(λn) is less than
1 since:
(a) We know that
α - pn/qn is less than
1/qn2 and greater than
-1/qn2. [From Theorem 2,
here]
(b) Multiplying
(qn)2 to all sides give us that:
α*(qn)2 - pnqn is between
-1 and
1.
(c) Multiplying
-1 to all sides give us that:
pnqn - α(qn)2 is between
-1 and
1.
(d) This proves that
λn is between
-1 and
1 or rather
absolute(λn) is less than
1.
(4) Inserting #2 into the formula for
An in Lemma 2 gives us:
An = a( λn-1/qn-1 + αqn-1)2 + b( λn-1/qn-1 + αqn-1)an-1 + c(qn-1)2Working this through and rearranging values gives us:
(qn-1)2(aα2 + bα + c) + 2aαλn-1 + a(λn-1)2/(qn-1)2 + bλn-1Since we know that
aα2 + bα + c = 0 (since
α is a quadratic number based on
a,b,c), we get:
An = 2aαλn-1 + a(λn-1)2/(qn-1)2 + bλn-1Since
absolute(λan-1) is less than
1, this tells us that:
absolute(An) is less than
2*absolute(aα) + absolute(a) + absolute(b).
To understand the details for why this is true, there are three cases to consider:
Case I:
a,b positive
In this case
An is less than
2*absolute(aα) + absolute(a) + absolute(b).
Case II:
a,b negative
In this case, the absolute values result in values the same as in Case I. In this case
An = -absolute(An).
Case III:
a,b: one is negative, one is positive
In this case,
An will be greater than
-absolute(An) and less than
absolute(An) so, then:
absolute(An) is less than
2*absolute(aα) + absolute(a) + absolute(b)Since
Cn = An-1, we know that:
absolute(Cn) is less than
2*absolute(aα) + absolute(a) + absolute(b)Finally, since
(Bn)2 = 4AnCn + b2-4ac, we know that:
(Bn)2 ≤ 4[ 2*absolute(aα) + absolute(a) + absolute(b)]2 + absolute(b2-4ac)(5) The important idea from all this is that there are only a finite number integers that
An, Bn, and
Cn can equal, that is, only those integers which make up the ranges in #4.
QED
Theorem 2: A continued fraction is periodic if and only if it represents an irrational quadratic number.(1) In Lemma 1, it was shown that a periodic continued fraction is a quadratic irrational number.
(2) Now, I will show that all quadratic irrational numbers are representable as periodic continued fractions.
(3) Let
α be a quadratic number (that is, an irrational that is a solution to a quadratic equation)
(4) We know that there are an infinite number of values
ai and
αi that make it up (from Theorem 1 above, otherwise it would not be irrational)
(5) But at each point, there are only a finite number of values
An, Bn, Cn that describe the equation that
αi solves.
(6) This means that it is inevitable that a specific combination
An, Bn, Cn repeats and continues to repeat.
(7) For each specific combination of
An, Bn, Cn, there are two possible real values that satisfy the equation. (This observation comes from the solution to the quadratic equation, found
here)
(8) So, eventually, some
αi repeats.
QED
Lemma 3: If a value is representeable by a finite continued fraction with an odd number of elements, then it is representable by an even number of elements and likewise if it is representable by an even number of elements, it can be represented by an odd number of elements.(1) Let
[a0, a1, ..., an] be a finite continued fraction of
n elements.
(2) Now, if
an ≥ 2, then:
[ a0, a1, ..., an] = [ a0, a1, ..., an-1,1 ](3) Otherwise, if
an = 1, then:
[ a0, a1, an-1,1 ] = [a0, a1, ... , an-1 + 1 ]QED