Interestingly, Bernoulli numbers may have been discovered earlier by Seki Kowa and were rediscovered independently by a 17-year-old Srinivasa Ramanujan.
Bernoulli was analyzing formulas for the sums of powers, that have the following form:
Sm(n) = ∑ (i=1, n) im
He looked at, for example:
S0(n) = n
S1(n) = (1/2)n2 - (1/2)n
S2(n) = (1/3)n3 - (1/2)n2 + (1/6)n
S3(n) = (1/4)n4 - (1/2)n3 + (1/4)n2
S4(n) = (1/5)n5 - (1/2)n4 + (1/3)n3 - (1/30)n
S5(n) = (1/6)n6 - (1/2)n5 + (5/12)n4 - (1/12)n2
S6(n) = (1/7)n7 - (1/2)n6 + (1/2)n5 - (1/6)n3 + (1/42)n.
S7(n) = (1/8)n8 - (1/2)n7 + (7/12)n6 - (7/24)n4 + (1/2)n2
S8(n) = (1/9)n9 - (1/2)n8 + (2/3)n7 - (7/15)n5 + (2/9)n3 - (1/30)n
S9(n) = (1/10)n10 - (1/2)n9 + (3/4)n8 - (7/10)n6 + (1/2)n4 - (3/20)n2
S10(n) = (1/11)n11 - (1/2)n10 + (5/6)n9 - n7 + n5 - (1/2)n3 + (5/66)n.
By looking at these formulas, he noticed a pattern and in analyzing this pattern, he came up with what were termed Bernoulli numbers by Abraham de Moivre.
Well, for each Sm(n), we can see that:
1) the first term is 1/(m+1)*nm+1
2) the second term, when it exists, is (-1/2)nm
3) the third term, when it exists, is (m/12)*nm-1
4) the fourth term, when it exists, is (-m)(m-1)(m-2)/720*nm-3
Bernoulli had discovered that if he defined a sequence of the numbers, he got a simple formula for defining the sum of powers.
The formula he discovered was the following:
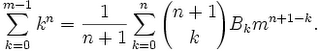
In the above formula, Bk refers to the sequence of Bernoulli numbers where Bernoulli numbers are defined in the following way:
Definition 1: Bernoulli Numbers

with B0 = 1.
As a convention, I will refer to Bernoulli numbers as Bi.
So, to figure out, B1, we have:

This gives us:
2*B0 + 2*B1 = 0
B1 = (1/2)[-2*B0] = (-1/2)(1) = (-1/2)
We determine B2 based on solving:

In this way, we find that:
B0 = 1
B1 = -(1/2)
B2 = (1/6)
B3 = 0
B4 = -(1/30)
B5 = 0
B6 = (1/42)
B7 = 0
B8 = -(1/30)
B9 = 0
B10 = (5/66)
B11 = 0
B12 = -(691/2730)
Bernoulli wrote that he was able to use his formula to compute S10(1000) in less than 10 minutes (see Smith, A Source Book in Mathematics, below).
Using his formula, this comes down to:
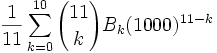
Evaluating this gives us:
91,409,924,241,424,243,424,241,924,242,500
I will now show a proof for Bernoulli's formula for sums. This is taken straight from Graham et al. Concrete Mathematics.
Definition 2: Sm(n)
Let Sm(n) = 0m + 1m + ... + (n-1)m
I will use this shorthand in the lemma and theorem below.
Postulate 1: 00 = 1
(This is taken from Graham et al.)
Graham et al argue in Concrete Mathematics that if we let 00 = 1, it provides a more elegant notation for the Binomial Theorem. Their argument is that the Binomial Theorem is very important while 00 is almost irrelevant. (see Concrete Mathematics, page 162).
Lemma 1:
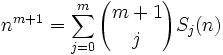
Proof:
(1) Sm+1(n) + nm+1 =
= ∑(k=0,n-1) km+1 + nm+1 =
= ∑(k=0,n) km+1 =
= 0m+1 + ∑(k=1,n) km+1 = ∑(k=1,n) km+1 =
= ∑ (k=0,n-1) (k+1)m+1
(2) Using the Binomial Theorem, we get:

(3) Putting this together with step #1 gives us:

This gives us:

(4) Since Sj(n) = oj + 1j + ... + (n-1)j, we have shown that:
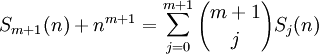
(5) Now, since
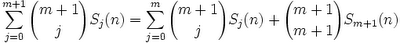
The conclusion follows from simple subtraction since [(m+1)!]/[(m+1)!(0)!] = 1.
QED
Theorem:
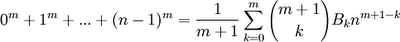
Proof:
(1) We can see that this is true for m=0 since:
S0 = n = (1/[1+1])∑ (k=0,0) ([0+1]!/k![1-k]!)Bkn0+1-k =
= (1)*(1!/[0!][1!])B0n1 = (1)*(1)*(1)*n = n [Since B0 = 1, see above]
(2) Let's assume that this is true up to m-1.
(3) Let Tm(n) =
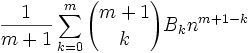
(4) Let Δ = Sm(n) - Tm(n)
(5) Using Lemma 1 above, we know that:
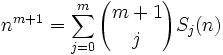
(6) Using our definition of Δ, we can also see that:
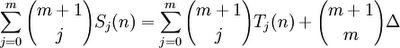
(7) The goal in this proof will be to show that Δ = 0.
(8) Adding the definition of Tj(n) [see step#3] gives us:

I also simplified [(m+1)!/(m!)(1!)] to (m+1).
(9) We can move all values that are independent of k before the ∑ (k=0,j):
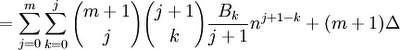
(10) Since we can change the order of the terms of a finite sum and still get the same result, we can switch each value of k with (j-k) to get:
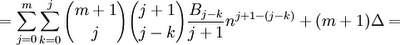
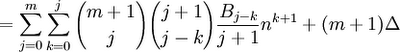
(11) Now, since (j+1) - (j-k) = k+1, we have:
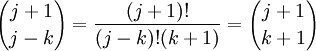
(12) Putting this result in step #11 gives us:
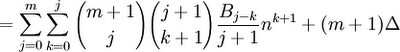
(13) We can see that in step #12, 0 ≤ k ≤ j ≤ m. The sum is in fact all combinations of j,k where this is the case. This means that we can rearrange the sum to the following:
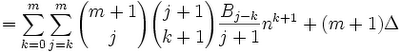
(14) Since nk+1 is independent of j, we can move it over to get the following:

(15) Since,

we can also rearrange the result in step #14 to give us:
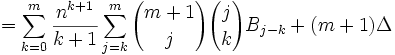
(16) Since:
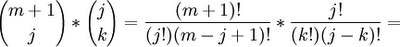

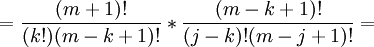

We can rearrange terms to get:
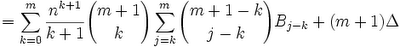
(17) Since:
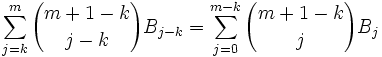
We can rearrange terms to get:
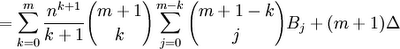
(18) Now, we know from the definition of Bernoulli numbers (see Definition 1 above) that

in all cases except where m = 0. This occurs only when k = m.
This allows us to simplify the result in step #17 to the following:
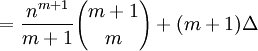
(19) Now since [(m+1)!/(m!)(1!)] = m+1, we get:
= nm+1 + (m+1)Δ
(20) But in step #5, we started out with nm+1 so we are left with:
nm+1 = nm+1 + (m+1)Δ.
(21) The only way that this is true is if Δ = 0.
QED
In another blog, I show how z/[ez - 1] can be used as a generating function for the Bernoulli numbers.
References
- Ronald L. Graham, Donald E. Knuth, Oren Patashnik, Concrete Mathematics, Addison-Wesley, 1989
- David Eugene Smith, A Source Book in Mathematics, Dover, 1959
- "Bernoulli Numbers", Wikipedia.Com
